Difference between Binary tree and B-tree
Last Updated :
12 May, 2022
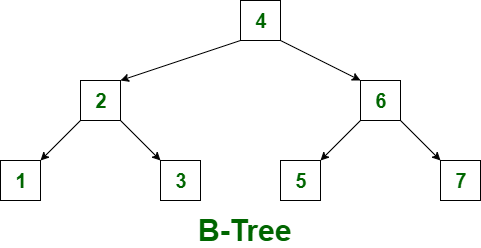
B-Tree : B-Tree is known as a self-balancing tree as its nodes are sorted in the inorder traversal. Unlike the binary trees, in B-tree, a node can have more than two children. B-tree has a height of logM N (Where ‘M’ is the order of tree and N is the number of nodes). And the height is adjusts automatically at each update. In the B-tree data is sorted in a specific order, with the lowest value on the left and the highest value on the right. To insert the data or key in B-tree is more complicated than binary tree.
There are some conditions that must be hold by the B-Tree:
- All the leaf nodes of the B-tree must be at the same level.
- Above the leaf nodes of the B-tree, there should be no empty sub-trees.
- B- tree’s height should lie as low as possible.
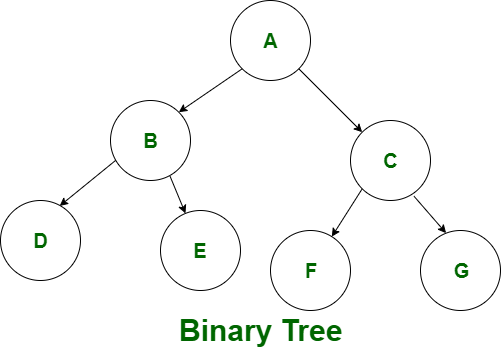
Binary Tree : A binary tree is the special type of general tree. Unlike B-tree, in a binary tree a node can have at most two nodes. In a binary tree, there is a limitation on the degree of a node because the nodes in a binary tree can’t have more than two child node(or degree two). The topmost node of a binary tree is called root node and there are mainly two subtrees one is left-subtree and another is right-sub-tree. Unlike the general tree, the binary tree can be empty. Like B-tree, binary tree can also be sorted in inorder traversal. But it can also be sorted in preorder as well as postorder. In binary tree, data insertion is not complicated than B-tree.
Let’s see the difference between B-tree and Binary tree:
| S.NO |
B-tree |
Binary tree |
| 1. |
In a B-tree, a node can have maximum ‘M'(‘M’ is the order of the tree) number of child nodes. |
While in binary tree, a node can have maximum two child nodes or sub-trees. |
| 2. |
B-tree is called a sorted tree as its nodes are sorted in inorder traversal. |
While binary tree is not a sorted tree. It can be sorted in inorder, preorder, or postorder traversal. |
| 3. |
B-tree has a height of log(M*N) (Where ‘M’ is the order of tree and N is the number of nodes). |
While binary tree has a height of log2(N) (Where N is the number of nodes). |
| 4. |
B-Tree is performed when the data is loaded into the disk. |
Unlike B-tree, binary tree is performed when the data is loaded in the RAM(faster memory). |
| 5. |
B-tree is used in DBMS(code indexing, etc). |
While binary tree is used in Huffman coding and Code optimization and many others. |
| 6. |
To insert the data or key in B-tree is more complicated than a binary tree. |
While in binary tree, data insertion is not more complicated than B-tree. |
| 7. |
B-tree is a self-balancing tree. The height of the tree is automatically adjusted on each update. |
A binary tree is not a self-balancing tree. |
Share your thoughts in the comments
Please Login to comment...