Diameter of a Binary Indexed Tree with N nodes

Given a Binary Indexed Tree with N nodes except root node 0 (Numbered from 1 to N), Find its diameter. 
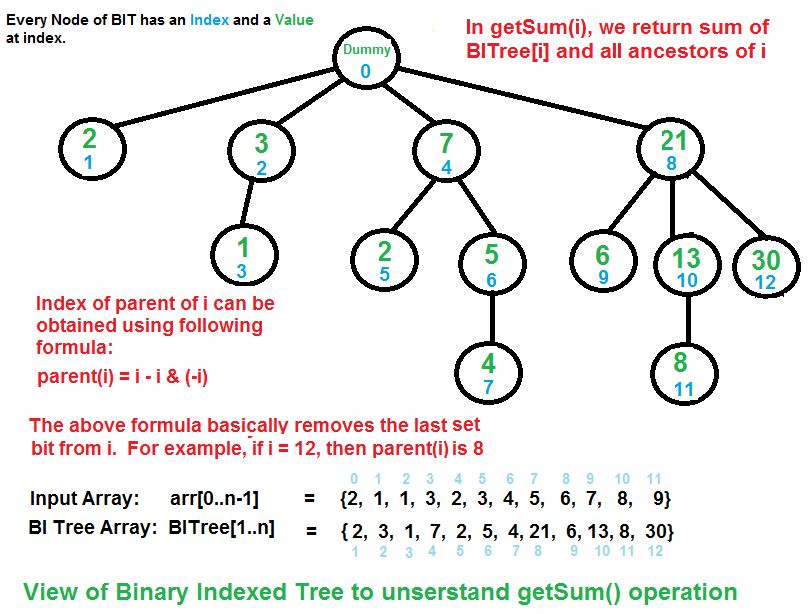
Binary Indexed Tree is a tree where parent of a node number X = X – (X & (X – 1)) i.e. last bit is unset in X. The diameter of a tree is the longest simple path between any two leaves. 
Examples:

Input: N = 12 
Output: 6 
Explanation: Path from node 7 to node 11.

Input : n = 15
Output : 7 

Approach:

• In a BIT, root is always node 0. In first level, all nodes are of power of 2 . (1, 2, 4, 8, ….)
• Consider any node in the first level (1, 2, 4, 8, ) its sub-tree will include all the nodes which has same number of bits as that of the root. 
  1. Sub-Tree with root 1 will have no child.
  2. Sub-Tree with root 2 will have 3 as a child.
  3. Sub-Tree with root 4 will have 5, 6, 7 as a child.
  4. Sub-Tree with root 8 will have 9, 10, 11, 12, 13, 14, 15 as a child. (Double the size of the previous subtree)
  5. So subtree with root K will have K nodes including root. And the height of each subtree would be equal: 
     • for subtree with root 1
     • for subtree with root 2
     • for subtree with root 4
• Now, we need to find the subtree in which N lies. Say, the height of subtree just before the subtree in which N lies is H and size is L. So, the following cases are possible : 
  • Case 1 : When N >= L*2 – 1, in such a scenario N is in last level of its subtree. Thus, the diameter will be 2*H + 1. (Path from the lowest level leaf of the previous subtree to the N ).
    
  • Case 2 : When N >= L + L/2 – 1, in such a scenario N is at level H in its subtree. Thus, diameter will be 2*H.
    
  • Case 3 : Otherwise, it is optimal to consider the maximum path length between leaf nodes of two subtree just before the subtree in which N lies i.e diameter is 2*H – 1.

Below are the implementation of the above approach: 

C++

#include <bits/stdc++.h>
using namespace std;

// Function to find diameter
// of BIT with N + 1 nodes
int diameter(int n)
{
    // L is size of subtree just before subtree
    // in which N lies
    int L, H, templen;
    L = 1;

    // H is the height of subtree just before
    // subtree in which N lies
    H = 0;

    // Base Cases
    if (n == 1) {
        return 1;
    }
    if (n == 2) {
        return 2;
    }
    if (n == 3) {
        return 3;
    }

    // Size of subtree are power of 2
    while (L * 2 <= n) {
        L *= 2;
        H++;
    }

    // 3 Cases as explained in Approach
    if (n >= L * 2 - 1)
        return 2 * H + 1;
    else if (n >= L + (L / 2) - 1)
        return 2 * H;
    return 2 * H - 1;
}

// Driver Code
int main()
{
    int n = 15;
    cout << diameter(n) << endl;
}

Java

// Java implementation of the approach
class GFG
{

// Function to find diameter
// of BIT with N + 1 nodes
static int diameter(int n)
{
    // L is size of subtree just before subtree
    // in which N lies
    int L, H, templen;
    L = 1;

    // H is the height of subtree just before
    // subtree in which N lies
    H = 0;

    // Base Cases
    if (n == 1) {
        return 1;
    }
    if (n == 2) {
        return 2;
    }
    if (n == 3) {
        return 3;
    }

    // Size of subtree are power of 2
    while (L * 2 <= n) {
        L *= 2;
        H++;
    }

    // 3 Cases as explained in Approach
    if (n >= L * 2 - 1)
        return 2 * H + 1;
    else if (n >= L + (L / 2) - 1)
        return 2 * H;
    return 2 * H - 1;
}

// Driver Code
public static void main(String []args)
{
    int n = 15;

    System.out.println(diameter(n));
}
}

// This code contributed by PrinciRaj1992

Python3

# Python3 implementation of the approach

# Function to find diameter
# of BIT with N + 1 nodes
def diameter(n):

    # L is size of subtree just before
    # subtree in which N lies
    L, H, templen = 0, 0, 0;
    L = 1;

    # H is the height of subtree just before
    # subtree in which N lies
    H = 0;

    # Base Cases
    if (n == 1):
        return 1;

    if (n == 2):
        return 2;

    if (n == 3):
        return 3;

    # Size of subtree are power of 2
    while (L * 2 <= n):
        L *= 2;
        H += 1;

    # 3 Cases as explained in Approach
    if (n >= L * 2 - 1):
        return 2 * H + 1;
    elif (n >= L + (L / 2) - 1):
        return 2 * H;
    return 2 * H - 1;

# Driver Code
n = 15;
print(diameter(n));

# This code is contributed by Rajput-Ji

C#

// C# implementation of the approach
using System;

class GFG
{

// Function to find diameter
// of BIT with N + 1 nodes
static int diameter(int n)
{
    // L is size of subtree just before subtree
    // in which N lies
    int L, H;
    L = 1;

    // H is the height of subtree just before
    // subtree in which N lies
    H = 0;

    // Base Cases
    if (n == 1)
    {
        return 1;
    }
    if (n == 2)
    {
        return 2;
    }
    if (n == 3)
    {
        return 3;
    }

    // Size of subtree are power of 2
    while (L * 2 <= n)
    {
        L *= 2;
        H++;
    }

    // 3 Cases as explained in Approach
    if (n >= L * 2 - 1)
        return 2 * H + 1;
    else if (n >= L + (L / 2) - 1)
        return 2 * H;
    return 2 * H - 1;
}

// Driver Code
public static void Main(String []args)
{
    int n = 15;

    Console.WriteLine(diameter(n));
}
}

// This code is contributed by 29AjayKumar

Javascript

<script>

// Function to find diameter
// of BIT with N + 1 nodes
function diameter(n)
{
    // L is size of subtree just before subtree
    // in which N lies
    var L, H, templen;
    L = 1;

    // H is the height of subtree just before
    // subtree in which N lies
    H = 0;

    // Base Cases
    if (n == 1) {
        return 1;
    }
    if (n == 2) {
        return 2;
    }
    if (n == 3) {
        return 3;
    }

    // Size of subtree are power of 2
    while (L * 2 <= n) {
        L *= 2;
        H++;
    }

    // 3 Cases as explained in Approach
    if (n >= L * 2 - 1)
        return 2 * H + 1;
    else if (n >= L + (L / 2) - 1)
        return 2 * H;
    return 2 * H - 1;
}

// Driver Code
var n = 15;
document.write( diameter(n));

</script>

Output:

7

Time Complexity: O(log n)

Auxiliary Space: O(1)