Diameter of a Binary Indexed Tree with N nodes
Last Updated :
08 Mar, 2022
Given a Binary Indexed Tree with N nodes except root node 0 (Numbered from 1 to N), Find its diameter.
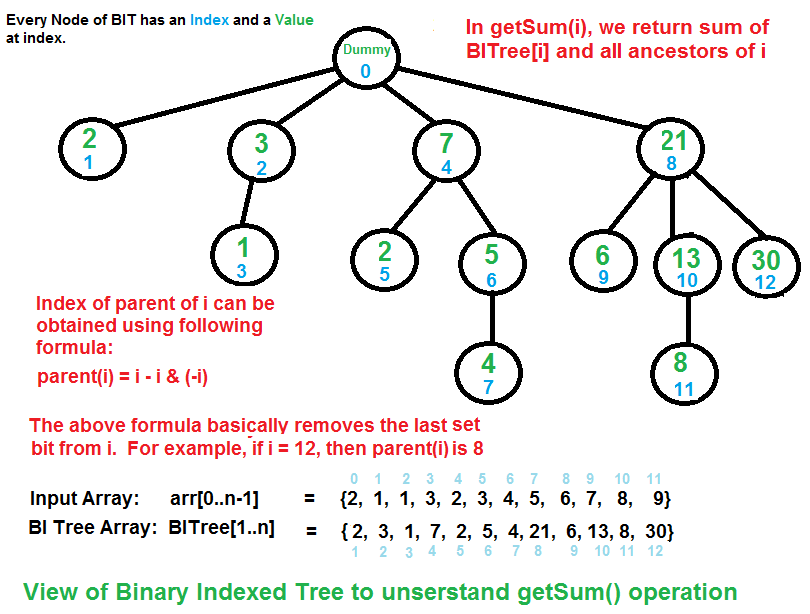
Binary Indexed Tree is a tree where parent of a node number X = X – (X & (X – 1)) i.e. last bit is unset in X. The diameter of a tree is the longest simple path between any two leaves.
Examples:
Input: N = 12
Output: 6
Explanation: Path from node 7 to node 11.
Input : n = 15
Output : 7
Approach:
- In a BIT, root is always node 0. In first level, all nodes are of power of 2 . (1, 2, 4, 8, ….)
- Consider any node in the first level (1, 2, 4, 8, ) its sub-tree will include all the nodes which has same number of bits as that of the root.
- Sub-Tree with root 1 will have no child.
- Sub-Tree with root 2 will have 3 as a child.
- Sub-Tree with root 4 will have 5, 6, 7 as a child.
- Sub-Tree with root 8 will have 9, 10, 11, 12, 13, 14, 15 as a child. (Double the size of the previous subtree)
- So subtree with root K will have K nodes including root. And the height of each subtree would be equal:
- for subtree with root 1
- for subtree with root 2
- for subtree with root 4
- Now, we need to find the subtree in which N lies. Say, the height of subtree just before the subtree in which N lies is H and size is L. So, the following cases are possible :
- Case 1 : When N >= L*2 – 1, in such a scenario N is in last level of its subtree. Thus, the diameter will be 2*H + 1. (Path from the lowest level leaf of the previous subtree to the N ).
- Case 2 : When N >= L + L/2 – 1, in such a scenario N is at level H in its subtree. Thus, diameter will be 2*H.
- Case 3 : Otherwise, it is optimal to consider the maximum path length between leaf nodes of two subtree just before the subtree in which N lies i.e diameter is 2*H – 1.
Below are the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int diameter(int n)
{
int L, H, templen;
L = 1;
H = 0;
if (n == 1) {
return 1;
}
if (n == 2) {
return 2;
}
if (n == 3) {
return 3;
}
while (L * 2 <= n) {
L *= 2;
H++;
}
if (n >= L * 2 - 1)
return 2 * H + 1;
else if (n >= L + (L / 2) - 1)
return 2 * H;
return 2 * H - 1;
}
int main()
{
int n = 15;
cout << diameter(n) << endl;
}
|
Java
class GFG
{
static int diameter(int n)
{
int L, H, templen;
L = 1;
H = 0;
if (n == 1) {
return 1;
}
if (n == 2) {
return 2;
}
if (n == 3) {
return 3;
}
while (L * 2 <= n) {
L *= 2;
H++;
}
if (n >= L * 2 - 1)
return 2 * H + 1;
else if (n >= L + (L / 2) - 1)
return 2 * H;
return 2 * H - 1;
}
public static void main(String []args)
{
int n = 15;
System.out.println(diameter(n));
}
}
|
Python3
def diameter(n):
L, H, templen = 0, 0, 0;
L = 1;
H = 0;
if (n == 1):
return 1;
if (n == 2):
return 2;
if (n == 3):
return 3;
while (L * 2 <= n):
L *= 2;
H += 1;
if (n >= L * 2 - 1):
return 2 * H + 1;
elif (n >= L + (L / 2) - 1):
return 2 * H;
return 2 * H - 1;
n = 15;
print(diameter(n));
|
C#
using System;
class GFG
{
static int diameter(int n)
{
int L, H;
L = 1;
H = 0;
if (n == 1)
{
return 1;
}
if (n == 2)
{
return 2;
}
if (n == 3)
{
return 3;
}
while (L * 2 <= n)
{
L *= 2;
H++;
}
if (n >= L * 2 - 1)
return 2 * H + 1;
else if (n >= L + (L / 2) - 1)
return 2 * H;
return 2 * H - 1;
}
public static void Main(String []args)
{
int n = 15;
Console.WriteLine(diameter(n));
}
}
|
Javascript
<script>
function diameter(n)
{
var L, H, templen;
L = 1;
H = 0;
if (n == 1) {
return 1;
}
if (n == 2) {
return 2;
}
if (n == 3) {
return 3;
}
while (L * 2 <= n) {
L *= 2;
H++;
}
if (n >= L * 2 - 1)
return 2 * H + 1;
else if (n >= L + (L / 2) - 1)
return 2 * H;
return 2 * H - 1;
}
var n = 15;
document.write( diameter(n));
</script>
|
Time Complexity: O(log n)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...