Designing Non-Deterministic Finite Automata (Set 3)

Prerequisite: Finite Automata Introduction
In this article, we will see some designing of Non-Deterministic Finite Automata (NFA).
Problem-1: Construction of a minimal NFA accepting a set of strings over {a, b} in which each string of the language starts with ‘ab’. 
Explanation: The desired language will be like: 

L1 = {ab, abba, abaa, ...........}

Here as we can see that each string of the above language starts with ‘ab’ and end with any alphabet either ‘a’ or ‘b’. 
But the below language is not accepted by this NFA because none of the string of below language starts with ‘ab’. 

L2 = {ba, ba, babaaa..............}

The state transition diagram of the desired language will be like below: 

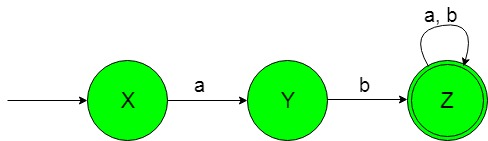
In the above NFA, the initial state ‘X’ on getting ‘a’ as the input it transits to a state ‘Y’. The state ‘Y’ on getting ‘b’ as the input it transits to a final state ‘Z’. The final state ‘Z’ on getting either ‘a’ or ‘b’ as the input it remains in the state of itself. 

Python Implementation:

Python3

def stateX(n):
    #if length of n become 0
    #then print not accepted
    if(len(n)==0):
        print("string not accepted")

    else:
        #if at zero index
        #'a' found call
        #stateY function
        if (n[0]=='a'):
            stateY(n[1:])

        #if at zero index
        #'b' then print
        #not accepted
        elif (n[0]=='b'):
            print("string not accepted")

def stateY(n):
    #if length of n become 0
    #then print not accepted
    if(len(n)==0):
        print("string not accepted")

    else:
        #if at zero index
        #'a' then print
        #not accepted
        if (n[0]=='a'):
            print("string not accepted")

        #if at zero index
        #'b' found call
        #stateZ function
        elif (n[0]=='b'):
            stateZ(n[1:])

def stateZ(n):
    #if length of n become 0
    #then print accepted
    if(len(n)==0):
        print("string accepted")

    else:
        #if at zero index
        #'b' found call
        #stateZ function
        if (n[0]=='a'):
            stateZ(n[1:])

        #if at zero index
        #'b' found call
        #stateZ function
        elif (n[0]=='b'):
            stateZ(n[1:])




#take input
n=input()

#call stateA function
#to check the input
stateX(n)

Problem-2: Construction of a minimal NFA accepting a set of strings over {a, b} in which each string of the language is not starting with ‘ab’. 
Explanation: The desired language will be like: 

L1 = {ba, bba, bbaa, ...........}

Here as we can see that each string of the above language is not starting with ‘ab’ but can end with either ‘a’ or ‘b’. 
But the below language is not accepted by this NFA because some of the string of below language starts with ‘ab’. 

L2 = {ab, aba, ababaab..............}

The state transition diagram of the desired language will be like below: 

In the above NFA, the initial state ‘X’ on getting ‘b’ as the input it transits to a state ‘Y’. The state ‘Y’ on getting either ‘a’ or ‘b’ as the input it transits to a final state ‘Z’. The final state ‘Z’ on getting either ‘a’ or ‘b’ as the input it remains in the state of itself. 

Python Implementation:

Python3

def stateX(n):
    #if length of n become 0
    #then print not accepted
    if(len(n)==0):
        print("string not accepted")

    else:
        #if at zero index
        #'a' found then
        #print not accepted
        if (n[0]=='a'):
            print("string not accepted")

        #if at zero index
        #'b' then call
        #stateY function
        elif (n[0]=='b'):
            stateY(n[1:])

def stateY(n):
    #if length of n become 0
    #then print not accepted
    if(len(n)==0):
        print("string not accepted")

    else:
        #if at zero index
        #'a' found call
        #stateZ function
        if (n[0]=='a'):
            stateZ(n[1:])

        #if at zero index
        #'b' found call
        #stateZ function
        elif (n[0]=='b'):
            stateZ(n[1:])

def stateZ(n):
    #if length of n become 0
    #then print accepted
    if(len(n)==0):
        print("string accepted")

    else:
        #if at zero index
        #'b' found call
        #stateZ function
        if (n[0]=='a'):
            stateZ(n[1:])

        #if at zero index
        #'b' found call
        #stateZ function
        elif (n[0]=='b'):
            stateZ(n[1:])




#take input
n=input()

#call stateA function
#to check the input
stateX(n)