Cube Root of Unity – Formula, Properties & Equation

Cube Root of Unity: The cube root of unity is represented as ∛1 and has three roots that are 1, ω, ω², which on multiplication answers unity (1). Among the cube roots of unity, one root is a real root (1) and the other two ω, ω² are imaginary roots.

In this article, we will learn about, the cube roots of unity i.e. 1^1/3 (or ∛1). Their definition and notation, the properties, and examples in detail.

What is the Cube Root of Unity?

Cube roots of unity (represented as 1^1/3 or ∛1) are 1, 𝛚, 𝛚². Here real root is 1 whereas 𝛚 and 𝛚² are the imaginary roots where one root is the square of the other. The imaginary root ‘𝛚’ is read as omega and ‘𝛚²‘ is read as omega square and their respective value are

• 𝛚 = ( -1 + i√3 )/2
• 𝛚² = ( -1 – i√3 )/2

Cube Root of Unity: Definition and Notation

Cube root of unity can be defined as an expression x³ – 1 = 0 ( or x= ∛1 ) and we solve it using the algebraic formula that is a³-b³ = (a-b)( a²+ ab +b²). This is a sub-concept of the chapter Complex Numbers in Mathematics that deals with the imaginary numbers that lie in the complex plane.

∛1 = ( 1 )^1/3 = 1, 𝛚, 𝛚²

where ‘𝛚’ and ‘𝛚^2′ are read as ‘omega‘ and ‘omega square‘ respectively.

Properties of Cube Root of Unity

A few properties of the cube root of unity are:

Among the three cube roots of unity, one is real and two are imaginary, i.e.

• 1 is the real root of unity.
• 𝛚 and 𝛚² are the imaginary roots of unity.

Also, the cube root of unity follows a specific pattern as,

• 1 + 𝛚 + 𝛚² = 0
• 1 × 𝛚 × 𝛚² = 𝛚³ = 1

Value of Omega and Omega Square

Omega and Omega Square are imaginary root of unity and their value is given as:

• 𝛚 = ( -1 + i√3 )/2
• 𝛚² = ( -1 – i√3 )/2

Product of Cube Root of Unity

Product of the cube roots of unity i.e. 1 , 𝛚 , 𝛚² is equal to 1.

1 × 𝛚 × 𝛚² = 1 × [( -1 + i√3 )/2] × [( -1 – i√3 )/2]

=> [(-1)² – ( i√3)² ] / (2 × 2)

=> ( 1 -3i² ) / 4

=> ( 1 – 3(-1) ) / 4 {i= √-1 and i² = -1}

=> 4 / 4

=> 1

Therefore 1 × 𝛚 × 𝛚² = 1

Sum of Cube Root of Unity

Sum of the cube roots of unity i.e. 1 , 𝛚 , 𝛚² is equal to zero( = 0 ).

1 + 𝛚 + 𝛚² = 1 + [( -1 + i√3 )/2] + [( -1 – i√3 )/2]

=> 1 + ( -1 + i√3 – 1 – i√3 )/2

=> 1 + (-2/2)

=> 1 – 1

=> 0

Therefore 1 + 𝛚 + 𝛚² = 0

How To Find Cube Root Of Unity?

To find cube root of unity , we will use the following algebraic formulas to find the cube root of unity:

• a³-b³=( a-b )( a²+ab+b² )…(i)

Lets consider the expression ∛1 = a

Taking cube on both sides, we get

=> 1 = a³

=> a³ – 1 = 0

=>(a – 1)(a² + a + 1) = 0 {By i}

a – 1 = 0 => a = 1

Solving quadratic equation: (a² + a + 1) = 0, we get

a = ( -1 + i√3 )/2 or ( -1 – i√3 )/2

Therefore we get the three cube roots of unity as 1, (-1 + i√3 )/2 and (-1 – i√3)/2 also written as 1, 𝛚, 𝛚² where

• 𝛚 = (-1 + i√3 )/2
• 𝛚² = (-1 – i√3 )/2

Geometric Interpretation of Cube Root of Unity

Geometric interpretation of cube roots of unity is points on the unit circle in the complex plane. They are all evenly spaced along the circumference of the circle, forming the vertices of a regular polygon with the origin as its centre.

This is an equilateral triangle that has its centroid located at the origin and a vertex at (1, 0) . The point (1, 0) corresponds to the complex number (1 + 0i) on the complex plane. This is one of the cube roots of unity and the other 2 cube roots of unity will be the remaining vertices of the equilateral triangle on the complex plane i.e. ( -1 + i√3 )/2 and ( -1 – i√3 )/2 represented as 𝛚, 𝛚² respectively ,corresponding to the points on the coordinate plane that is (-1/2 ,√3/2) and (-1/2 ,-√3/2).

Cube Root of Unity

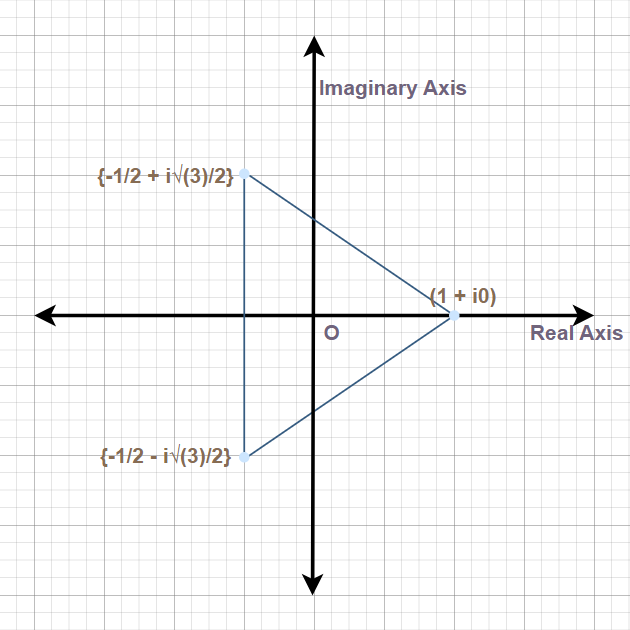
Formula for Cube Root of Unity

Some formulas related to complex numbers that can be used to represent the cube roots of unity in simpler terms are:

Euler’s Formula

Euler’s Formula shows the relation between the imaginary power of exponent and trigonometric ratio sin and cos and is given by:

e^ix = cos x + i sin x

The cube roots of unity are 1, 𝛚, 𝛚² where 𝛚 = ( -1 + i√3 )/2 and 𝛚² = ( -1 – i√3 )/2 . Using Euler’s Formula, we can conclude the following:

• 1 = e⁰ⁱ [as e⁰ⁱ = cos(0) + i sin(0) = 1 + i(0) = 1]
• 𝛚 = e^2π/3i [as e^2π/3i = cos (2π/3) + i sin (2π/3) = (-1 + i√3)/2]
• 𝛚²= e^4π/3i [as e^4π/3i = cos (4π/3) + i sin (4π/3) = (-1 – i√3)/2]

Note: Cube roots of unity i.e. 1, 𝛚, 𝛚² form a G.P. with common difference ratio equal to 𝛚 and their arguments 0,2π/3,4π/3 form A.P. with common difference equal to 2π/3.

De Moivre’s Formula

De Moivre’s Formula expresses the n^th power of a complex number in polar form and is given by:

(cos x + i sin x)ⁿ = cos (nx) + i.sin (nx), n ⋿ Q

Using Euler’s Formula, we know e^ix = cos x + i sin x

So we can also say

(cos x + i sin x)ⁿ = (e^ix)ⁿ = e^inx = cos (nx) + i sin (nx), n ⋿ Q

Deriving Cube Roots of Unity by De Moivre’s Theorem

To find cube roots of unity using De Moivre’s Formula , follow the given steps:

Step 1: Lets assume z = 1 ^1/n = (cos 0 + i sin 0)^1/n [n ⋿ N and n ≧ 2]

Using Polar form where we take x = |z|cos θ and y = |z|sin θ

Step 2: Add 2kπ in the arguments where k ⋿ I, so we get

z = 1 ^1/n = {cos(2kπ) + i sin(2kπ)}^1/n

Step 3: Apply De Moivre’s Formula,

z = cos[(2kπ)/n] + i sin[(2kπ)/n] = e ^i(2kπ/n)

Step 4: Take k = 0, 1, 2, 3, …. upto n-1 which makes up n values for k

Step 5: To find cube roots of unity , we have n = 3 then n-1 = 2

Put n = 0, 1, 2 in z = e ^i(2kπ/n) expression, we get z = e⁰ⁱ, e^2π/3i, e^4π/3i respectively. These can also be represented as 1, 𝛚, 𝛚²

Therefore the cube roots of unity are 1, 𝛚, 𝛚²

People Also Read:

• Dividing Complex Numbers
• Z Bar in Complex Numbers

Summary – Cube Root of Unity – Formula, Properties

The cube roots of unity are fundamental in the study of complex numbers, particularly within the mathematical field of geometry. They are represented as 1, ω, ω², where 1 is the real root and ω and ω² are the imaginary roots, with ω = (-1 + i√3) / 2 and ω² = (-1 – i√3) / 2.

Cube Root Of Unity Solved Examples

Example 1: Prove that a³ + b³ = (a+b)(a+b𝛚 )(a+b𝛚²)

Solution:

We know that,

• a³+b³ = (a+b)(a²-ab+b²)
• 𝛚 + 𝛚² = -1

=> L.H.S = a³-b³ = (a+b)(a²+ (𝛚 + 𝛚²)ab + b²)

= (a+b)(a² + 𝛚ab + 𝛚²ab+b²)

= (a+b)(a² + 𝛚ab + 𝛚²ab+𝛚³b² ) { By 𝛚³=1 }

= (a+b)(a(a+b𝛚) + 𝛚²b(a+b𝛚))

= (a+b)(a+b𝛚)(a+𝛚²)

= R.H.S

Hence proved

Example 2: Solve 5 + 𝛚 + 𝛚² + 𝛚³

Solution:

We know that,

• 1 + 𝛚 + 𝛚² = 0
• 𝛚³ = 1

= 5 + 𝛚 + 𝛚² + 𝛚³

= 4 +1 + 𝛚 + 𝛚² + 1

= 4 + 0 + 1

= 5

Practice Questions on Cube Root of Unity

Q1: Prove the following:

• a³ – b³ = (a – b)(a – b𝛚)(a – b𝛚²)
• a³ + b³ + c³ – 3abc = (a + b + c)(a + b𝛚 + c𝛚²)(a + b𝛚² + c𝛚)

Q2: Find the roots for z = 1^(1/4) using De Moivre’s Formula

Q3: Prove that (1 + ω)³ – (1 + ω²)³ = 0

FAQs on Cube Root of Unity

What are Cube Root of Unity ?

Cube Root of Unity are found by solving z = 1^(1/3) expression and we get 1, 𝛚, 𝛚² as the roots.

What is Sum of Cube Root of Unity ?

Sum of cube roots of unity i.e. 1, 𝛚, 𝛚² is equal to zero (= 0).

What is Product of Cube Root of Unity ?

Product of cube roots of unity i.e. 1, 𝛚, 𝛚² is equal to 1.

What are properties of Cube Root of Unity?

Properties of the cube root of unity are:

• 1 + 𝛚 + 𝛚² = 0
• 𝛚^3p + 𝛚^3p+1 + 𝛚^3p+2 = 0 for p = 1, 2, 3,…
• 1 × 𝛚 × 𝛚² = 𝛚³ = 1

How to calculate Cube Roots of Unity?

To find cube roots of unity, you may use the following methods:

• By Euler’s Formula
• By De Moivre’s Formula