Cross Product of Vectors in R Programming
Last Updated :
25 Aug, 2020
In mathematics, the cross product or also known as the vector product is a binary operation on two vectors in three-dimensional space and is denoted by the symbol ‘X‘. Given two linearly independent vectors a and b, the cross product, a × b is a vector that is perpendicular to both a and b and thus normal to the plane containing them.
Let we have given two vectors,
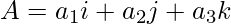
and,
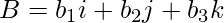
where,
i: the unit vector along the x directions
j: the unit vector along the y directions
k: the unit vector along the z directions
Then the cross product is calculated as:
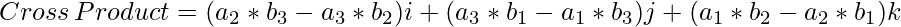
where,
![Rendered by QuickLaTeX.com [(a_2 * b_3 - a_3 * b_2), (a_3 * b_1 - a_1 * b_3), (a_1 * b_2 - a_2 * b_1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-25354d3555d2fcc340d2231e40c979fa_l3.png)
are the coefficient of unit vector along i, j and k directions.
Example:
Given two vectors A and B as,
A = 3i + 5j + 4k,
and
B = 2i + 7j + 5k
Cross Product = (5 ? 5 – 4 ? 7)i + (4 ? 2 – 3 ? 5)j + (3 ? 7 – 5 ? 2)k
= (?3)i + (?7)j + (11)k
Computing Cross Product in R
R language provides a very efficient method to calculate the cross product of two vectors. By using cross() method which is available in the pracma library. This function computes the cross or vector product of vectors in 3 dimensions. In the case of matrices, it takes the first dimension of length 3 and computes the cross product between corresponding columns or rows.
Syntax: cross(x, y)
Parameters:
x: numeric vector or matrix
y: numeric vector or matrix
# Taking Input as Vectors
Example 1:
R
library(pracma)
a = c(3, 5, 4)
b = c(2, 7, 5)
print(cross(a, b))
|
Output:
[1] -3 -7 11
Example 2:
R
library(pracma)
a = c(23, 15, 49)
b = c(28, 17, 25)
print(cross(a, b))
|
Output:
[1] -458 797 -29
# Taking Input as Matrix
Example 1:
R
library(pracma)
a = matrix(
c(1, 2, 3, 4, 5, 6, 7, 8, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
b = matrix(
c(5, 2, 1, 4, 6, 6, 3, 2, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
print(cross(a, b))
|
Output:
[, 1] [, 2] [, 3]
[1, ] -4 14 -8
[2, ] -6 0 4
[3, ] 54 -36 -10
Example 2:
R
library(pracma)
a = matrix(
c(11, 2, 31, 4, 52, 64, 7, 8, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
b = matrix(
c(85, 21, 1, 4, 61, 6, 32, 2, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
print(cross(a, b))
|
Output:
[, 1] [, 2] [, 3]
[1, ] -649 2624 61
[2, ] -3592 232 36
[3, ] 54 225 -242
Share your thoughts in the comments
Please Login to comment...