Dot Product of Vectors in R Programming
Last Updated :
18 May, 2023
In mathematics, the dot product or also known as the scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number. Let us given two vectors A and B, and we have to find the dot product of two vectors.
Given that,
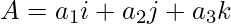
and,
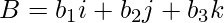
where,
- i: the unit vector along the x directions
- j: the unit vector along the y directions
- k: the unit vector along the z directions
Then the dot product is calculated as:
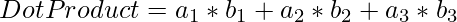
Example:
Given two vectors A and B as,
A = 3i + 5j + 4k,
and
B = 2i + 7j + 5k
Dot Product = 3 * 2 + 5 * 7 + 4 * 5 = 6 + 35 + 20 + 61
Computing Dot Product in R
R language provides a very efficient method to calculate the dot product of two vectors. By using dot() method which is available in the geometry library one can do so.
Syntax: dot(x, y, d = NULL)
Parameters:
x: Matrix of vectors
y: Matrix of vectors
d: Dimension along which to calculate the dot product
Return: Vector with length of dth dimension
Example 1:
R
library(geometry)
a = 5
b = 7
print(dot(a, b, d = TRUE))
|
Output:
[1] 35
Example 2:
To determine b’s complex conjugate, we utilize the Conj() function. In our example, the Conj() function is provided by the pracma package, which we first install and load. Then, a and b, two complex numbers, are defined. The formula a1 * b1_conjugate + a2 * b2_conjugate +… is used to calculate the dot product of these two vectors, where b_conjugate is b’s complex conjugate.
R
install.packages("pracma")
library(pracma)
a <- 3 + 1i
b <- 7 + 6i
dot_prod <- sum(a * Conj(b))
print(dot_prod)
|
Output:
[1] 27-11i
Example 3:
R
library(geometry)
a = c(1, 4)
b = c(7, 4)
print(dot(a, b, d = TRUE))
|
Output:
[1] 23
Example 4:
In the following example let’s take two 2D arrays and calculate the dot product of these two. To create a 2D array in R please refer Multidimensional Array in R.
R
library(geometry)
vector1 = c(2, 1)
vector2 = c(0, 3)
a = array(c(vector1, vector2), dim = c(2, 2))
vector1 = c(4, 2)
vector2 = c(9, 3)
b = array(c(vector1, vector2), dim = c(2, 2))
print(dot(a, b, d = TRUE))
|
Output:
[1] 10 9
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...