Skip to content
Related Articles

Related Articles

Table of Contents

Improve Article
Save Article
Like Article

Count possible permutations of given array satisfying the given conditions

  • Last Updated : 27 Apr, 2021

Given an array, arr[] consisting of N distinct elements, the task is to count possible permutations of the given array that can be generated which satisfies the following properties: 

  • The two halves must be sorted.
  • arr[i] must be less than arr[N / 2 + i]

Note: N is always even and indexing starts from 0.

Examples:

Input: arr[] = {10, 20, 30, 40} 
Output: 2 
Explanation: 
Possible permutations of the given array that satisfy the given conditions are:{{10, 20, 30, 40}, {10, 30, 20, 40}}. 
Therefore, the required output is 2. 

Input: arr[] = {1, 2}
Output: 1

Approach: Follow the steps below to solve the problem: 



  • Initialize a variable, say cntPerm to store the count of permutations of the given array that satisfy the given condition.
  • Find the value of the binomial coefficient of 2NCN using the following formula:

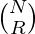\binom{N}{R} = [{N × (N – 1) × …………. × (N – R + 1)} / {(R × (R – 1) × ….. × 1)}]  

  • Finally, calculate catalan number = 2NCN / (N + 1) and print it as the required answer.

Below is the implementation of the above approach: 

C++




// C++ Program to implement
// the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to get the value
// of binomial coefficient
int binCoff(int N, int R)
{
    // Stores the value of
    // binomial coefficient
    int res = 1;
 
    if (R > (N - R)) {
 
        // Since C(N, R)
        // = C(N, N - R)
        R = (N - R);
    }
 
    // Calculate the value
    // of C(N, R)
    for (int i = 0; i < R; i++) {
        res *= (N - i);
        res /= (i + 1);
    }
    return res;
}
 
// Function to get the count of
// permutations of the array
// that satisfy the condition
int cntPermutation(int N)
{
    // Stores count of permutations
    // of the array that satisfy
    // the given condition
    int cntPerm;
 
    // Stores the value of C(2N, N)
    int C_2N_N = binCoff(2 * N, N);
 
    // Stores the value of
    // catalan number
    cntPerm = C_2N_N / (N + 1);
 
    // Return answer
    return cntPerm;
}
 
// Driver Code
int main()
{
 
    int arr[] = { 1, 2, 3, 4 };
    int N = sizeof(arr) / sizeof(arr[0]);
    cout << cntPermutation(N / 2);
 
    return 0;
}
Java



// Java Program to implement
// the above approach
import java.io.*;
class GFG{
  
// Function to get the value
// of binomial coefficient
static int binCoff(int N,
                   int R)
{
  // Stores the value of
  // binomial coefficient
  int res = 1;
 
  if (R > (N - R))
  {
    // Since C(N, R)
    // = C(N, N - R)
    R = (N - R);
  }
 
  // Calculate the value
  // of C(N, R)
  for (int i = 0; i < R; i++)
  {
    res *= (N - i);
    res /= (i + 1);
  }
  return res;
}
 
// Function to get the count of
// permutations of the array
// that satisfy the condition
static int cntPermutation(int N)
{
  // Stores count of permutations
  // of the array that satisfy
  // the given condition
  int cntPerm;
 
  // Stores the value of C(2N, N)
  int C_2N_N = binCoff(2 * N, N);
 
  // Stores the value of
  // catalan number
  cntPerm = C_2N_N / (N + 1);
 
  // Return answer
  return cntPerm;
}
  
// Driver Code
public static void main (String[] args)
{
  int arr[] = {1, 2, 3, 4};
  int N = arr.length;
  System.out.println(cntPermutation(N / 2));
}
}
 
// This code is contributed by sanjoy_62
Python3



# Python3 program to implement
# the above approach
 
# Function to get the value
# of binomial coefficient
def binCoff(N, R):
     
    # Stores the value of
    # binomial coefficient
    res = 1
 
    if (R > (N - R)):
 
        # Since C(N, R)
        # = C(N, N - R)
        R = (N - R)
 
    # Calculate the value
    # of C(N, R)
    for i in range(R):
        res *= (N - i)
        res //= (i + 1)
 
    return res
 
# Function to get the count of
# permutations of the array
# that satisfy the condition
def cntPermutation(N):
     
    # Stores count of permutations
    # of the array that satisfy
    # the given condition
 
    # Stores the value of C(2N, N)
    C_2N_N = binCoff(2 * N, N)
 
    # Stores the value of
    # catalan number
    cntPerm = C_2N_N // (N + 1)
 
    # Return answer
    return cntPerm
 
# Driver Code
if __name__ == '__main__':
     
    arr = [ 1, 2, 3, 4 ]
    N = len(arr)
     
    print(cntPermutation(N // 2))
 
# This code is contributed by mohit kumar 29
C#



// C# Program to implement
// the above approach
using System;
class GFG{
  
// Function to get the value
// of binomial coefficient
static int binCoff(int N,
                   int R)
{
  // Stores the value of
  // binomial coefficient
  int res = 1;
 
  if (R > (N - R))
  {
    // Since C(N, R)
    // = C(N, N - R)
    R = (N - R);
  }
 
  // Calculate the value
  // of C(N, R)
  for (int i = 0; i < R; i++)
  {
    res *= (N - i);
    res /= (i + 1);
  }
  return res;
}
 
// Function to get the count of
// permutations of the array
// that satisfy the condition
static int cntPermutation(int N)
{
  // Stores count of permutations
  // of the array that satisfy
  // the given condition
  int cntPerm;
 
  // Stores the value of C(2N, N)
  int C_2N_N = binCoff(2 * N, N);
 
  // Stores the value of
  // catalan number
  cntPerm = C_2N_N / (N + 1);
 
  // Return answer
  return cntPerm;
}
  
// Driver Code
public static void Main(String[] args)
{
  int []arr = {1, 2, 3, 4};
  int N = arr.Length;
  Console.WriteLine(cntPermutation(N / 2));
}
}
 
// This code is contributed by shikhasingrajput
Javascript



<script>
// javascript Program to implement
// the above approach
 
    // Function to get the value
    // of binomial coefficient
    function binCoff(N , R) {
        // Stores the value of
        // binomial coefficient
        var res = 1;
 
        if (R > (N - R)) {
            // Since C(N, R)
            // = C(N, N - R)
            R = (N - R);
        }
 
        // Calculate the value
        // of C(N, R)
        for (i = 0; i < R; i++) {
            res *= (N - i);
            res /= (i + 1);
        }
        return res;
    }
 
    // Function to get the count of
    // permutations of the array
    // that satisfy the condition
    function cntPermutation(N) {
        // Stores count of permutations
        // of the array that satisfy
        // the given condition
        var cntPerm;
 
        // Stores the value of C(2N, N)
        var C_2N_N = binCoff(2 * N, N);
 
        // Stores the value of
        // catalan number
        cntPerm = C_2N_N / (N + 1);
 
        // Return answer
        return cntPerm;
    }
 
    // Driver Code
     
        var arr = [ 1, 2, 3, 4 ];
        var N = arr.length;
        document.write(cntPermutation(N / 2));
 
// This code contributed by umadevi9616
</script>
Output
2
Time Complexity: O(N)
Auxiliary Space: O(1)



My Personal Notes
arrow_drop_up
Previous
Print even and odd numbers in a given range using recursion
Next

Rearrange given binary strings to maximize their Bitwise XOR value
Recommended Articles
Page :
Count number of coordinates from an array satisfying the given conditions
30, Apr 21
Count valid pairs in the array satisfying given conditions
11, Dec 18
Count all possible N-length vowel permutations that can be generated based on the given conditions
17, Dec 20
Number of K's such that the given array can be divided into two sets satisfying the given conditions
29, Oct 19
Lexicographically smallest permutation of length 2N that can be obtained from an N-length array satisfying given conditions
17, Jun 21
Generate N integers satisfying the given conditions
06, Sep 19
Split N as the sum of K numbers satisfying the given conditions
21, Aug 20
Sort a permutation of first N Natural Numbers by swapping pairs satisfying given conditions
09, Jun 21
Maximize occupied cells in given Matrix satisfying the conditions
11, Jan 22
Count permutations of all integers upto N that can form an acyclic graph based on given conditions
13, Oct 20
Maximum possible sum of squares of stack elements satisfying the given properties
09, Oct 20
Generate all binary permutations such that there are more or equal 1's than 0's before every point in all permutations
17, Aug 14
Count of N digit numbers possible which satisfy the given conditions
11, Jul 19
Count of Binary Strings possible as per given conditions
30, Jul 20
Count of pairs satisfying the given condition
22, Jan 20
Queries to count distinct Binary Strings of all lengths from N to M satisfying given properties
30, Jul 20
Count of distinct permutations of every possible length of given string
20, Aug 20
Count of Ordered Pairs (X, Y) satisfying the Equation 1/X + 1/Y = 1/N
14, Aug 20
Count of numbers satisfying m + sum(m) + sum(sum(m)) = N
12, Oct 17
Maximum modified Array sum possible by choosing elements as per the given conditions
19, Aug 20
Find all possible unique indices after reducing the array based on given conditions
10, Sep 21
Maximum possible value of array elements that can be made based on given capacity conditions
27, Sep 21
Count of possible permutations of a number represented as a sum of 2's, 4's and 6's only
31, May 20
Count permutations possible by replacing '?' characters in a Binary String
03, Mar 21
Article Contributed By :
https://media.geeksforgeeks.org/auth/avatar.png
shashanktrivedi02
@shashanktrivedi02
Vote for difficulty





Improved By :
Article Tags :
Practice Tags :
Report Issue

We use cookies to ensure you have the best browsing experience on our website. By using our site, you
acknowledge that you have read and understood our
Cookie Policy &
        Privacy Policy

Lightbox

Start Your Coding Journey Now!