Count of the non-prime divisors of a given number
Last Updated :
01 Nov, 2023
Given a number N, the task is to find the count of non-prime divisors of the given number N.
Examples:
Input: N = 8
Output: 3
Explanation:
Divisors of 8 are – {1, 2, 4, 8}
Non-Prime Divisors – {1, 4, 8}
Input: N = 20
Output: 4
Explanation:
Divisors of 20 are – {1, 2, 4, 5, 10, 20}
Non-Prime Divisors – {1, 4, 10, 20}
Approach: The key observation in the problem is that any number can be written as a product of its prime factors as
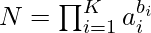
where K is the count of the prime factors of the given number. Using permutation and combination we can find that the total count of the
factors that are
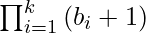
Therefore, the count of the non-prime factors will be:
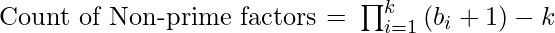
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
vector<int> getFactorization(int x)
{
int count = 0;
vector<int> v;
while (x % 2 == 0) {
count++;
x = x / 2;
}
if (count != 0)
v.push_back(count);
for (int i = 3; i <= sqrt(x); i += 2) {
count = 0;
while (x % i == 0) {
count++;
x /= i;
}
if (count != 0)
v.push_back(count);
}
if (x > 1) {
v.push_back(1);
}
return v;
}
int nonPrimeDivisors(int N)
{
vector<int> v = getFactorization(N);
int ret = 1;
for (int i = 0; i < v.size(); i++)
ret = ret * (v[i] + 1);
ret = ret - v.size();
return ret;
}
int main()
{
int N = 8;
cout << nonPrimeDivisors(N) << endl;
return 0;
}
|
Java
import java.util.*;
class GFG{
static Vector<Integer> getFactorization(int x)
{
int count = 0;
Vector<Integer> v = new Vector<>();
while (x % 2 == 0)
{
count++;
x = x / 2;
}
if (count != 0)
v.add(count);
for (int i = 3;
i <= Math.sqrt(x); i += 2)
{
count = 0;
while (x % i == 0)
{
count++;
x /= i;
}
if (count != 0)
v.add(count);
}
if (x > 1)
{
v.add(1);
}
return v;
}
static int nonPrimeDivisors(int N)
{
Vector<Integer> v = getFactorization(N);
int ret = 1;
for (int i = 0; i < v.size(); i++)
ret = ret * (v.get(i) + 1);
ret = ret - v.size();
return ret;
}
public static void main(String[] args)
{
int N = 8;
System.out.println(nonPrimeDivisors(N));
}
}
|
Python3
from math import sqrt
def getFactorization(x):
count = 0
v = []
while (x % 2 == 0):
count += 1
x = x // 2
if (count != 0):
v.append(count)
for i in range(3, int(sqrt(x)) + 12):
count = 0
while (x % i == 0):
count += 1
x //= i
if (count != 0):
v.append(count)
if (x > 1):
v.append(1)
return v
def nonPrimeDivisors(N):
v = getFactorization(N)
ret = 1
for i in range(len(v)):
ret = ret * (v[i] + 1)
ret = ret - len(v)
return ret
if __name__ == '__main__':
N = 8
print(nonPrimeDivisors(N))
|
C#
using System;
using System.Collections.Generic;
class GFG{
static List<int> getFactorization(int x)
{
int count = 0;
List<int> v = new List<int>();
while (x % 2 == 0)
{
count++;
x = x / 2;
}
if (count != 0)
v.Add(count);
for (int i = 3;
i <= Math.Sqrt(x); i += 2)
{
count = 0;
while (x % i == 0)
{
count++;
x /= i;
}
if (count != 0)
v.Add(count);
}
if (x > 1)
{
v.Add(1);
}
return v;
}
static int nonPrimeDivisors(int N)
{
List<int> v = getFactorization(N);
int ret = 1;
for (int i = 0; i < v.Count; i++)
ret = ret * (v[i] + 1);
ret = ret - v.Count;
return ret;
}
public static void Main(String[] args)
{
int N = 8;
Console.WriteLine(nonPrimeDivisors(N));
}
}
|
Javascript
<script>
function getFactorization(x)
{
let count = 0;
let v = [];
while (x % 2 == 0)
{
count++;
x = Math.floor(x / 2);
}
if (count != 0)
v.push(count);
for (let i = 3;
i <= Math.floor(Math.sqrt(x)); i += 2)
{
count = 0;
while (x % i == 0)
{
count++;
x = Math.floor(x / i);
}
if (count != 0)
v.push(count);
}
if (x > 1)
{
v.push(1);
}
return v;
}
function nonPrimeDivisors(N)
{
let v = getFactorization(N);
let ret = 1;
for (let i = 0; i < v.length; i++)
ret = ret * (v[i] + 1);
ret = ret - v.length;
return ret;
}
let N = 8;
document.write(nonPrimeDivisors(N));
</script>
|
Approach 2:
One approach is to check all the divisors of the given number and count the divisors that are not prime.
Algorithm:
Initialize a count variable to 0.
For each number i from 1 to N, check if i is a divisor of N.
If i is a divisor of N, check if it is prime.
If i is not prime, increment the count variable.
Return the count variable.
C++
#include <iostream>
#include <cmath> // needed for sqrt() function
using namespace std;
bool is_prime(int n) {
if (n <= 1) {
return false;
}
for (int i = 2; i <= sqrt(n); i++) {
if (n % i == 0) {
return false;
}
}
return true;
}
int count_non_prime_divisors(int N) {
int count = 0;
for (int i = 1; i <= N; i++) {
if (N % i == 0) {
if (!is_prime(i)) {
count += 1;
}
}
}
return count;
}
int main() {
int N = 20;
cout << "Number of non-prime divisors of " << N << " is " << count_non_prime_divisors(N) << endl;
return 0;
}
|
Java
import java.util.*;
public class Main {
public static boolean isPrime(int n)
{
if (n <= 1) {
return false;
}
for (int i = 2; i <= Math.sqrt(n); i++) {
if (n % i == 0) {
return false;
}
}
return true;
}
public static int countNonPrimeDivisors(int N)
{
int count = 0;
for (int i = 1; i <= N; i++) {
if (N % i == 0) {
if (!isPrime(i)) {
count += 1;
}
}
}
return count;
}
public static void main(String[] args)
{
int N = 20;
System.out.println("Number of non-prime divisors of " + N + " is " + countNonPrimeDivisors(N));
}
}
|
Python3
def count_non_prime_divisors(N):
count = 0
for i in range(1, N+1):
if N % i == 0:
if is_prime(i) == False:
count += 1
return count
def is_prime(n):
if n <= 1:
return False
for i in range(2, int(n**0.5)+1):
if n % i == 0:
return False
return True
N = 20
print("Number of non-prime divisors of", N, "is", count_non_prime_divisors(N))
|
C#
using System;
class GFG {
static bool IsPrime(int n) {
if (n <= 1) {
return false;
}
for (int i = 2; i <= Math.Sqrt(n); i++) {
if (n % i == 0) {
return false;
}
}
return true;
}
static int CountNonPrimeDivisors(int N) {
int count = 0;
for (int i = 1; i <= N; i++) {
if (N % i == 0) {
if (!IsPrime(i)) {
count += 1;
}
}
}
return count;
}
static void Main() {
int N = 20;
Console.WriteLine("Number of non-prime divisors of " + N + " is " + CountNonPrimeDivisors(N));
}
}
|
Javascript
function isPrime(n) {
if (n <= 1) {
return false;
}
for (let i = 2; i <= Math.sqrt(n); i++) {
if (n % i === 0) {
return false;
}
}
return true;
}
function countNonPrimeDivisors(N) {
let count = 0;
for (let i = 1; i <= N; i++) {
if (N % i === 0) {
if (!isPrime(i)) {
count += 1;
}
}
}
return count;
}
let N = 20;
console.log(`Number of non-prime divisors of ${N} is ${countNonPrimeDivisors(N)}`);
|
OutputNumber of non-prime divisors of 20 is 4
Time Complexity: O(N * sqrt(N)), as we need to check all the divisors of N and for each divisor, we check if it is prime, which takes O(sqrt(N)) time.
Auxiliary Space: O(1), as we are not using any extra space.
Share your thoughts in the comments
Please Login to comment...