Count of pairs in Array with difference equal to the difference with digits reversed
Last Updated :
15 Nov, 2021
Given an array arr[] of N integers, the task is to find the number of pairs of array elements (arr[i], arr[j]) such that the difference between the pairs is equal to the difference when the digits of both the numbers are reversed.
Examples:
Input: arr[] = {42, 11, 1, 97}
Output: 2
Explanation:
The valid pairs of array elements are (42, 97), (11, 1) as:
1. 42 – 97 = 24 – 79 = (-55)
2. 11 – 1 = 11 – 1 = (10)
Input: arr[] = {1, 2, 3, 4}
Output: 6
Approach: The given problem can be solved by using Hashing which is based on the following observations:
A valid pair (i, j) will follow the equation as
=> arr[i] – arr[j] = rev(arr[i]) – rev(arr[j])
=> arr[i] – rev(arr[i]) = arr[j] – rev(arr[j])
Follow the below steps to solve the problem:
- Now, create a function reverseDigits, which will take an integer as an argument and reverse the digits of that integer.
- Store the frequency of values arr[i] – rev(arr[i]) in an unordered map, say mp.
- For each key(= difference) of frequency X the number of pairs that can be formed is given by
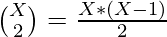 .
. - The total count of pairs is given by the sum of the value of the above expression for each frequency stored in the map mp.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int reverseDigits(int n)
{
string s = to_string(n);
reverse(s.begin(), s.end());
return stoi(s);
}
int countValidPairs(vector<int> arr)
{
long long res = 0;
unordered_map<int, int> mp;
for (int i = 0; i < arr.size(); i++) {
mp[arr[i] - reverseDigits(arr[i])]++;
}
for (auto i : mp) {
long long int t = i.second;
res += t * (t - 1) / 2;
}
return res;
}
int main()
{
vector<int> arr = { 1, 2, 3, 4 };
cout << countValidPairs(arr);
return 0;
}
|
Java
import java.util.HashMap;
class GFG {
public static int reverseDigits(int n)
{
String s = String.valueOf(n);
s = new StringBuffer(s).reverse().toString();
return Integer.parseInt(s);
}
public static int countValidPairs(int[] arr)
{
int res = 0;
HashMap<Integer, Integer> mp = new HashMap<Integer, Integer>();
for (int i = 0; i < arr.length; i++) {
if (mp.containsKey(arr[i] - reverseDigits(arr[i]))) {
mp.put(arr[i] - reverseDigits(arr[i]), mp.get(arr[i] - reverseDigits(arr[i])) + 1);
} else {
mp.put(arr[i] - reverseDigits(arr[i]), 1);
}
}
for (int i : mp.keySet()) {
int t = mp.get(i);
res += t * (t - 1) / 2;
}
return res;
}
public static void main(String args[])
{
int[] arr = { 1, 2, 3, 4 };
System.out.println(countValidPairs(arr));
}
}
|
Python3
def reverseDigits(n):
s = str(n)
s = "".join(reversed(s))
return int(s)
def countValidPairs(arr):
res = 0
mp = {}
for i in range(0, len(arr)):
if not arr[i] - reverseDigits(arr[i]) in mp:
mp[arr[i] - reverseDigits(arr[i])] = 1
else:
mp[arr[i] - reverseDigits(arr[i])] += 1
for i in mp:
t = mp[i]
res += (t * (t - 1)) // 2
return res
if __name__ == "__main__":
arr = [1, 2, 3, 4]
print(countValidPairs(arr))
|
C#
using System;
using System.Collections.Generic;
class GFG {
public static int reverseDigits(int n)
{
string s = n.ToString();
char[] arr = s.ToCharArray();
Array.Reverse(arr);
string st = new string(arr);
return Int32.Parse(st);
}
public static int countValidPairs(int[] arr)
{
int res = 0;
Dictionary<int, int> mp
= new Dictionary<int, int>();
for (int i = 0; i < arr.Length; i++) {
if (mp.ContainsKey(arr[i]
- reverseDigits(arr[i]))) {
mp[arr[i] - reverseDigits(arr[i])]
= mp[arr[i] - reverseDigits(arr[i])]
+ 1;
}
else {
mp[arr[i] - reverseDigits(arr[i])] = 1;
}
}
foreach(int i in mp.Keys)
{
int t = mp[i];
res += t * (t - 1) / 2;
}
return res;
}
public static void Main()
{
int[] arr = { 1, 2, 3, 4 };
Console.WriteLine(countValidPairs(arr));
}
}
|
Javascript
<script>
function reverseDigits(n)
{
let s = new String(n);
s = s.split("").reverse().join("");
return parseInt(s);
}
function countValidPairs(arr)
{
let res = 0;
let mp = new Map();
for (let i = 0; i < arr.length; i++) {
let temp = arr[i] - reverseDigits(arr[i]);
if (mp.has(temp)) {
mp.set(temp, mp.get(temp) + 1);
} else {
mp.set(temp, 1);
}
}
for (i of mp) {
let t = i[1];
res += (t * (t - 1)) / 2;
}
return res;
}
let arr = [1, 2, 3, 4];
document.write(countValidPairs(arr));
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(N)
Share your thoughts in the comments
Please Login to comment...