Count of all possible Paths in a Tree such that Node X does not appear before Node Y
Last Updated :
15 Sep, 2021
Given a Tree consisting of N nodes having values in the range [0, N – 1] and (N – 1) edges, and two nodes X and Y, the task is to find the number of possible paths in the Tree such that the node X does not appear before the node Y in the path.
Examples:
Input: N = 5, A = 2, B = 0, Edges[][] = { {0, 1}, {1, 2}, {1, 3}, {0, 4} }
Output: 18
Explanation:
Since (X, Y) and (Y, X) are being considered different, so the count of all possible paths connecting any two pairs of vertices = 2 * 5C2 = 20.
Out of these 20 pairs, those paths cannot be chosen, which consist of both nodes 2 and 0 as well as Node 2 appearing before Node 0.
There are two such paths (colored as green) which are shown below:
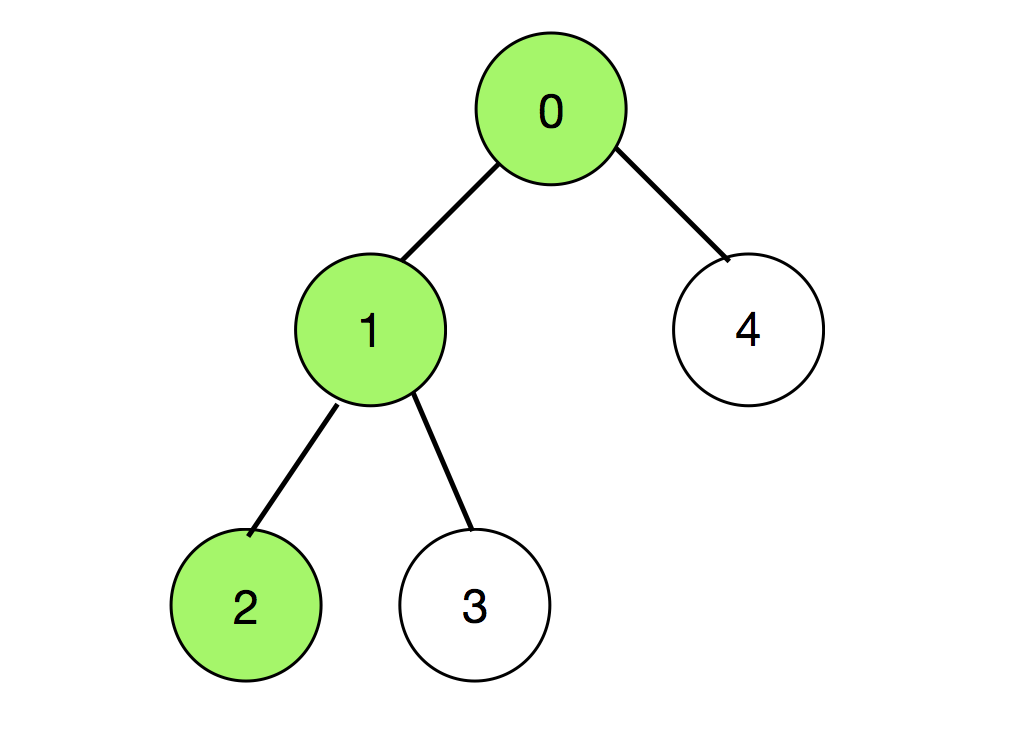
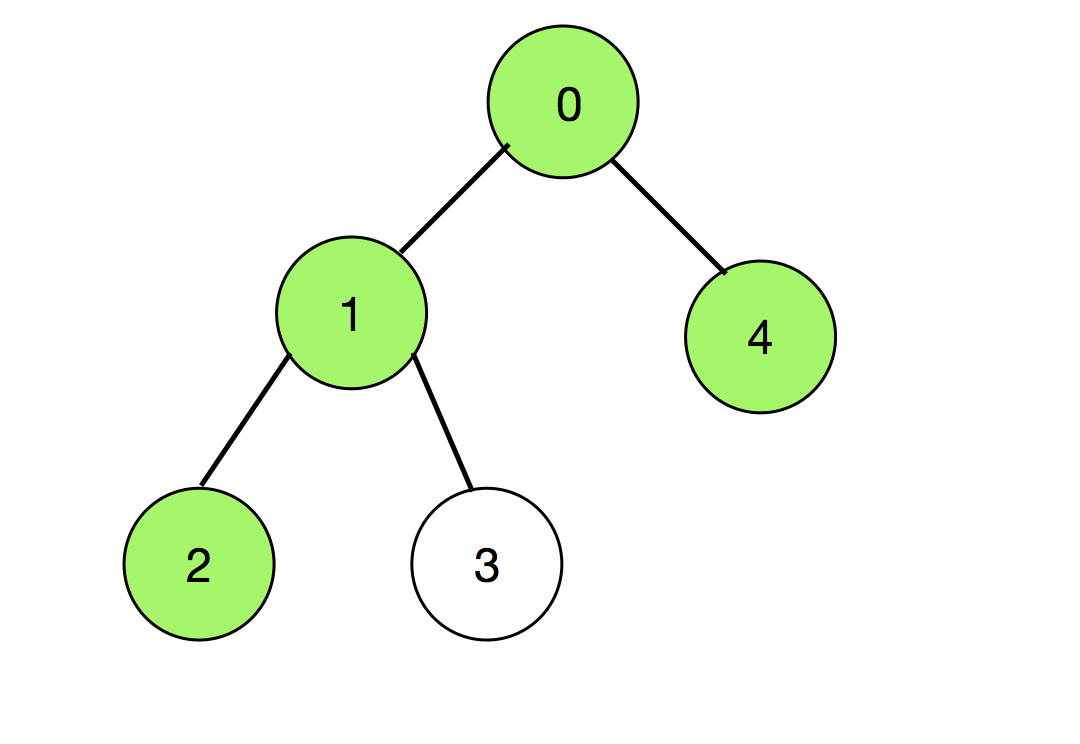
So there are total 20 – 2 = 18 such paths.
Input: N = 9, X = 5, Y = 3, Edges[][] = { {0, 2}, {1, 2}, {2, 3}, {3, 4}, {4, 6}, {4, 5}, {5, 7}, {5, 8} }
Output: 60
Explanation:
Since (X, Y) and (Y, X) are being considered different, so the count of all possible paths connecting any two pairs of vertices = N * (N – 1) = 9 * 8 = 72.
On observing the diagram below, any path starting from a Node in the subtree of Node 5, denoted by black, connecting to the vertices passing through the Node 3, denoted by green, will always have 5 appearing before 3 in the path.
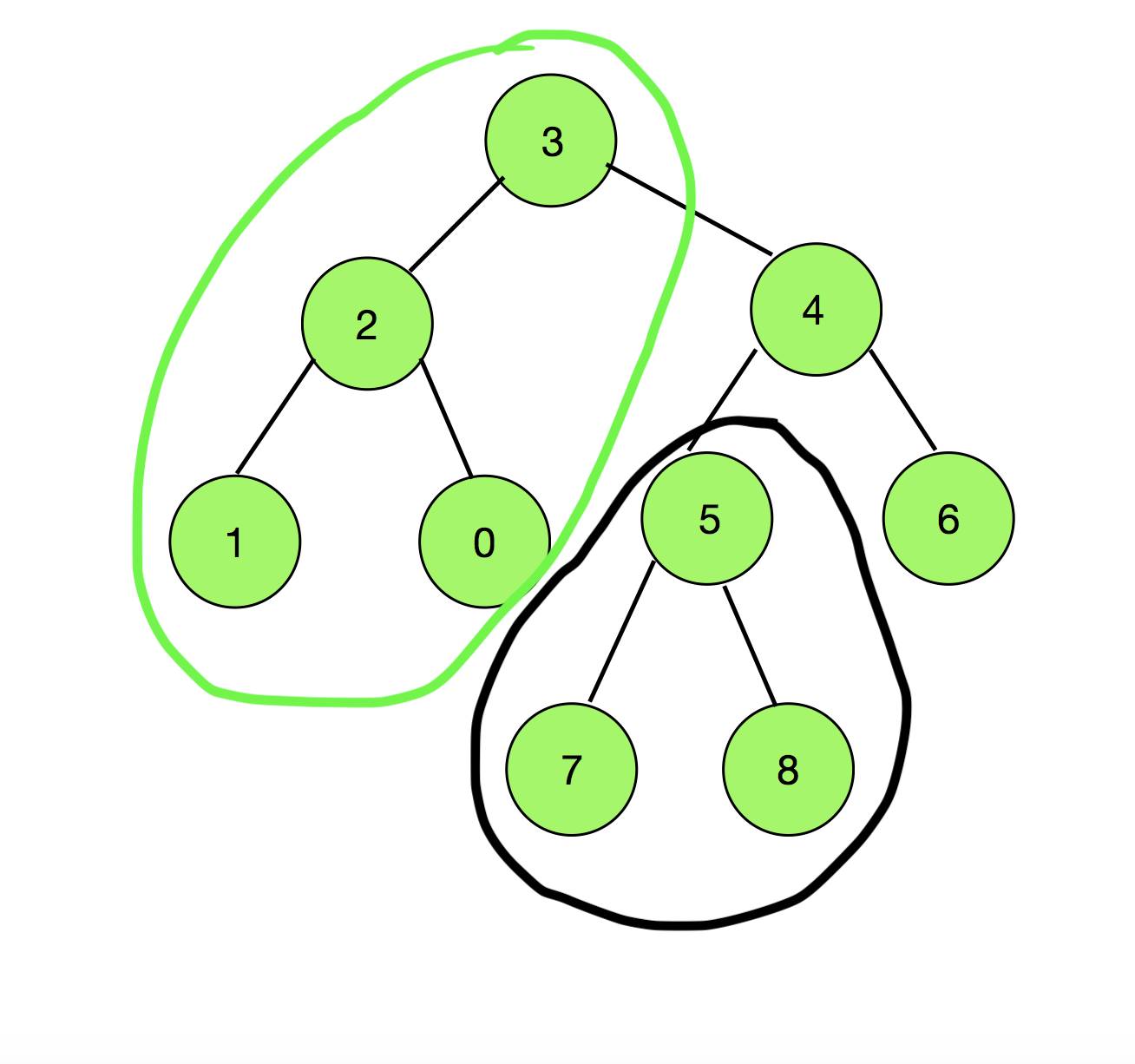
Therefore, total number of possible paths = (Total Nodes grouped in black) * (Total Nodes grouped in green) = 3 * 4 = 12.
Therefore, the final answer = 72 – 12 = 60
Approach:
The idea is to find the combination of node pairs that will always have the Node X appearing before Node Y in the path connecting them. Then, subtract the count of such pairs from the total number of possible node pairs = NC2. Consider node Y as the root node. Now any path which first encounters X and then Y, starts from the node in the subtree of node X and ends at a node in the sub-tree of node Y but not in the subtree of node W, where W is an immediate child of node Y and lies between X and Y in these paths.
Therefore, the final answer can be calculated by:
Count = N * (N – 1) – size_of_subtree(X) * (size_of_subtree(Y) – size_of_subtree(W))
If Y is taken as the root of the tree. Then, size_of_subtree(Y) = N.
Count = N * (N – 1) – size_of_subtree(X) * (N- size_of_subtree(W))
Follow the steps below to solve the problem:
- Initialize arrays subtree_size [], visited [] and check_subtree [] each of size N + 1. Initialize elements of visited [] as 0.
- Perform the DFS Traversal with Y as the root node to fill the check_subtree[] and subtree_size [] for each node. The check_subtree[] checks whether the subtree of the current node contains node X or not.
- Find the child(say node v) of Y which is in the path from X to Y. Initialize an integer variable say difference.
- Assign (total number of nodes – subtree_size[v] ) to difference.
- Return (N * (N – 1) ) – (subtree_size[A] * (difference)) as the answer.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
#define int long long int
using namespace std;
const int NN = 3e5;
vector<int> G[NN + 1];
int dfs(int node, int A, int* subtree_size,
int* visited, int* check_subtree)
{
visited[node] = true;
subtree_size[node] = 1;
if (node == A) {
check_subtree[node] = true;
}
else
check_subtree[node] = false;
for (int v : G[node]) {
if (!visited[v]) {
subtree_size[node]
+= dfs(v, A, subtree_size,
visited, check_subtree);
check_subtree[node] = check_subtree[node]
| check_subtree[v];
}
}
return subtree_size[node];
}
void addedge(int node1, int node2)
{
G[node1].push_back(node2);
G[node2].push_back(node1);
}
int numberOfPairs(int N, int B, int A)
{
int subtree_size[N + 1];
int visited[N + 1];
memset(visited, 0, sizeof(visited));
int check_subtree[N + 1];
dfs(B, A, subtree_size,
visited, check_subtree);
int difference;
for (int v : G[B]) {
if (check_subtree[v]) {
difference = N - subtree_size[v];
break;
}
}
return (N * (N - 1))
- difference * (subtree_size[A]);
}
int32_t main()
{
int N = 9;
int X = 5, Y = 3;
addedge(0, 2);
addedge(1, 2);
addedge(2, 3);
addedge(3, 4);
addedge(4, 6);
addedge(4, 5);
addedge(5, 7);
addedge(5, 8);
cout << numberOfPairs(N, Y, X);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int NN = (int) 3e5;
static Vector<Integer> []G = new Vector[NN + 1];
static int dfs(int node, int A, int[] subtree_size,
int[] visited, int[] check_subtree)
{
visited[node] = 1;
subtree_size[node] = 1;
if (node == A)
{
check_subtree[node] = 1;
}
else
check_subtree[node] = 0;
for (int v : G[node])
{
if (visited[v] == 0)
{
subtree_size[node] += dfs(v, A, subtree_size,
visited, check_subtree);
check_subtree[node] = check_subtree[node] |
check_subtree[v];
}
}
return subtree_size[node];
}
static void addedge(int node1, int node2)
{
G[node1].add(node2);
G[node2].add(node1);
}
static int numberOfPairs(int N, int B, int A)
{
int []subtree_size = new int[N + 1];
int []visited = new int[N + 1];
int []check_subtree = new int[N + 1];
dfs(B, A, subtree_size,
visited, check_subtree);
int difference = 0;
for (int v : G[B])
{
if (check_subtree[v] > 0)
{
difference = N - subtree_size[v];
break;
}
}
return (N * (N - 1)) -
difference * (subtree_size[A]);
}
public static void main(String[] args)
{
int N = 9;
int X = 5, Y = 3;
for (int i = 0; i < G.length; i++)
G[i] = new Vector<Integer>();
addedge(0, 2);
addedge(1, 2);
addedge(2, 3);
addedge(3, 4);
addedge(4, 6);
addedge(4, 5);
addedge(5, 7);
addedge(5, 8);
System.out.print(numberOfPairs(N, Y, X));
}
}
|
Python3
NN = int(3e5)
G = []
for i in range(NN + 1):
G.append([])
def dfs(node, A, subtree_size,
visited, check_subtree):
visited[node] = True
subtree_size[node] = 1
if (node == A):
check_subtree[node] = True
else:
check_subtree[node] = False
for v in G[node]:
if (not visited[v]):
subtree_size[node] += dfs(v, A,
subtree_size,
visited,
check_subtree)
check_subtree[node] = (check_subtree[node] |
check_subtree[v])
return subtree_size[node]
def addedge(node1, node2):
G[node1] += [node2]
G[node2] += [node1]
def numberOfPairs(N, B, A):
subtree_size = [0] * (N + 1)
visited = [0] * (N + 1)
check_subtree = [0] * (N + 1)
dfs(B, A, subtree_size,
visited, check_subtree)
difference = 0
for v in G[B]:
if (check_subtree[v]):
difference = N - subtree_size[v]
break
return ((N * (N - 1)) -
difference * (subtree_size[A]))
N = 9
X = 5
Y = 3
addedge(0, 2)
addedge(1, 2)
addedge(2, 3)
addedge(3, 4)
addedge(4, 6)
addedge(4, 5)
addedge(5, 7)
addedge(5, 8)
print(numberOfPairs(N, Y, X))
|
C#
using System;
using System.Collections.Generic;
class GFG{
static int NN = (int) 3e5;
static List<int> []G = new List<int>[NN + 1];
static int dfs(int node, int A, int[] subtree_size,
int[] visited, int[] check_subtree)
{
visited[node] = 1;
subtree_size[node] = 1;
if (node == A)
{
check_subtree[node] = 1;
}
else
check_subtree[node] = 0;
foreach (int v in G[node])
{
if (visited[v] == 0)
{
subtree_size[node] += dfs(v, A, subtree_size,
visited, check_subtree);
check_subtree[node] = check_subtree[node] |
check_subtree[v];
}
}
return subtree_size[node];
}
static void addedge(int node1, int node2)
{
G[node1].Add(node2);
G[node2].Add(node1);
}
static int numberOfPairs(int N, int B, int A)
{
int []subtree_size = new int[N + 1];
int []visited = new int[N + 1];
int []check_subtree = new int[N + 1];
dfs(B, A, subtree_size,
visited, check_subtree);
int difference = 0;
foreach (int v in G[B])
{
if (check_subtree[v] > 0)
{
difference = N - subtree_size[v];
break;
}
}
return (N * (N - 1)) -
difference * (subtree_size[A]);
}
public static void Main(String[] args)
{
int N = 9;
int X = 5, Y = 3;
for (int i = 0; i < G.Length; i++)
G[i] = new List<int>();
addedge(0, 2);
addedge(1, 2);
addedge(2, 3);
addedge(3, 4);
addedge(4, 6);
addedge(4, 5);
addedge(5, 7);
addedge(5, 8);
Console.Write(numberOfPairs(N, Y, X));
}
}
|
Javascript
<script>
let NN = 3e5;
let G = new Array(NN + 1);
function dfs(node, A, subtree_size, visited, check_subtree)
{
visited[node] = 1;
subtree_size[node] = 1;
if (node == A)
{
check_subtree[node] = 1;
}
else
check_subtree[node] = 0;
for (let v = 0; v < G[node].length; v++)
{
if (visited[G[node][v]] == 0)
{
subtree_size[node] += dfs(G[node][v], A, subtree_size,
visited, check_subtree);
check_subtree[node] = check_subtree[node] |
check_subtree[G[node][v]];
}
}
return subtree_size[node];
}
function addedge(node1, node2)
{
G[node1].push(node2);
G[node2].push(node1);
}
function numberOfPairs(N, B, A)
{
let subtree_size = new Array(N + 1);
subtree_size.fill(0);
let visited = new Array(N + 1);
visited.fill(0);
let check_subtree = new Array(N + 1);
check_subtree.fill(0);
dfs(B, A, subtree_size, visited, check_subtree);
let difference = 0;
for (let v = 0; v < G[B].length; v++)
{
if (check_subtree[G[B][v]] > 0)
{
difference = N - subtree_size[G[B][v]];
break;
}
}
return (N * (N - 1)) -
difference * (subtree_size[A]);
}
let N = 9;
let X = 5, Y = 3;
for (let i = 0; i < G.length; i++)
G[i] = [];
addedge(0, 2);
addedge(1, 2);
addedge(2, 3);
addedge(3, 4);
addedge(4, 6);
addedge(4, 5);
addedge(5, 7);
addedge(5, 8);
document.write(numberOfPairs(N, Y, X));
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(N)
Share your thoughts in the comments
Please Login to comment...