Check whether the cost of going from any node to any other node via all possible paths is same
Last Updated :
10 Mar, 2023
Given adjacency list representation of a directed graph, the task is to check whether the cost of going from any vertex to any other vertex via all possible paths is equal or not. If there is a cost c for going from vertex A to vertex B, then the cost to travel from vertex B to vertex A will be -c.
Examples:
Input: arr[][] = {{0, 2, 0, 1}, {-2, 0, 1, 0}, {0, -1, 0, -2}, {-1, 0, 2, 0}}
Output: Yes
Explanation:

Here the cost of going from any node to any other node is equal for all possible paths. For example, if we go from 1 to 4 via (1 -> 2 -> 3 -> 4) whose cost is (2 + 1 + (-2)) i.e. 1 and via ( 1 -> 4 ) which is a reverse edge whose cost is 1. Similarly, the cost for all other paths is equal.
Input: arr[][] = {{0, 1, 0, 3, 0}, {-1, 0, 3, 0, 4}, {0, -3, 0, 1, 1}, {-3, 0, -1, 0, 0}, {0, -4, -1, 0, 0}}
Output: No
Explanation:
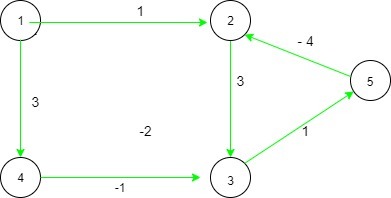
For the following two paths from edge 1 to 4, (1 -> 2 -> 3 -> 4), Cost = (1 + 3 + 1) = 5 and (1 -> 4), Cost = 3. Since the costs are difference, the answer is No
Approach: The idea is to maintain two arrays dis[] which maintains the distance of the paths travelled and visited[] which maintains the visited vertices. The graph is stored using 2D vector of pairs. The first value of the pair is the destination node and the second value is the cost associated with it. Now, DFS is run on the graph. The following two conditions occur for every vertex:
- If the next node to reach is not visited, then the dis array is updated with the value dis[current_node] + cost of the new edge found from the 2D vector i.e. current node to next node to reach and the same function is called with the unvisited same node.
- If the node is visited, then the distance of the next node to reach is compared with the dis[curr] + cost of edge to reach the next node. If they are equal, then the boolean variable flag is updated with true and the loop is continued for the next vertices.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
vector<pair<int, int> > adj[100005];
int vis[100005] = { 0 },
dist[100005] = { 0 },
flg;
void dfs(int curr)
{
vis[curr] = 1;
for (int i = 0; i < adj[curr].size(); i++) {
if (vis[adj[curr][i].first]) {
if (dist[adj[curr][i].first]
!= dist[curr] + adj[curr][i].second)
flg = 1;
}
else {
dist[adj[curr][i].first] = dist[curr]
+ adj[curr][i].second;
dfs(adj[curr][i].first);
}
}
}
int main()
{
int n = 4, m = 4;
flg = 0;
adj[0].push_back({ 1, 2 });
adj[1].push_back({ 0, -2 });
adj[1].push_back({ 2, 1 });
adj[2].push_back({ 1, -1 });
adj[2].push_back({ 3, -2 });
adj[3].push_back({ 2, 2 });
adj[3].push_back({ 0, -1 });
adj[0].push_back({ 3, 1 });
for (int i = 0; i < n; i++) {
if (flg)
break;
if (!vis[i])
dfs(i);
}
if (flg)
cout << "No" << endl;
else
cout << "Yes" << endl;
return 0;
}
|
Java
import java.util.*;
class GFG {
static class pair {
int first, second;
public pair(int first, int second) {
this.first = first;
this.second = second;
}
}
static Vector<pair>[] adj = new Vector[100005];
static int[] vis = new int[100005];
static int[] dist = new int[100005];
static int flg;
static void dfs(int curr) {
vis[curr] = 1;
for (int i = 0; i < adj[curr].size(); i++) {
if (vis[adj[curr].get(i).first] > 0) {
if (dist[adj[curr].get(i).first] !=
dist[curr] + adj[curr].get(i).second)
flg = 1;
} else {
dist[adj[curr].get(i).first] =
dist[curr] + adj[curr].get(i).second;
dfs(adj[curr].get(i).first);
}
}
}
public static void main(String[] args) {
int n = 4, m = 4;
flg = 0;
for (int i = 0; i < adj.length; i++) {
adj[i] = new Vector<pair>();
}
adj[0].add(new pair(1, 2));
adj[1].add(new pair(0, -2));
adj[1].add(new pair(2, 1));
adj[2].add(new pair(1, -1));
adj[2].add(new pair(3, -2));
adj[3].add(new pair(2, 2));
adj[3].add(new pair(0, -1));
adj[0].add(new pair(3, 1));
for (int i = 0; i < n; i++) {
if (flg == 1)
break;
if (vis[i] != 1)
dfs(i);
}
if (flg == 1)
System.out.print("No" + "\n");
else
System.out.print("Yes" + "\n");
}
}
|
Python3
adj = [[] for i in range(100005)]
vis = [0]*100005
dist = [0]*100005
flg = 0
def dfs(curr):
vis[curr] = 1
for i in range(len(adj[curr])):
if (vis[adj[curr][i][0]]):
if (dist[adj[curr][i][0]]
!= dist[curr] + adj[curr][i][1]):
flg = 1
else:
dist[adj[curr][i][0]] = dist[curr]+ adj[curr][i][1]
dfs(adj[curr][i][0])
n = 4
m = 4
flg = 0
adj[0].append([1, 2])
adj[1].append([0, -2])
adj[1].append([2, 1])
adj[2].append([1, -1])
adj[2].append([3, -2])
adj[3].append([2, 2])
adj[3].append([0, -1])
adj[0].append([3, 1])
for i in range(n):
if (flg):
break
if (vis[i] == 0):
dfs(i)
if (flg):
print("No")
else:
print("Yes")
|
C#
using System;
using System.Collections.Generic;
class GFG {
class pair {
public int first, second;
public pair(int first, int second) {
this.first = first;
this.second = second;
}
}
static List<pair>[] adj = new List<pair>[100005];
static int[] vis = new int[100005];
static int[] dist = new int[100005];
static int flg;
static void dfs(int curr) {
vis[curr] = 1;
for (int i = 0; i < adj[curr].Count; i++) {
if (vis[adj[curr][i].first] > 0) {
if (dist[adj[curr][i].first] !=
dist[curr] + adj[curr][i].second)
flg = 1;
} else {
dist[adj[curr][i].first] =
dist[curr] + adj[curr][i].second;
dfs(adj[curr][i].first);
}
}
}
public static void Main(String[] args) {
int n = 4;
flg = 0;
for (int i = 0; i < adj.Length; i++) {
adj[i] = new List<pair>();
}
adj[0].Add(new pair(1, 2));
adj[1].Add(new pair(0, -2));
adj[1].Add(new pair(2, 1));
adj[2].Add(new pair(1, -1));
adj[2].Add(new pair(3, -2));
adj[3].Add(new pair(2, 2));
adj[3].Add(new pair(0, -1));
adj[0].Add(new pair(3, 1));
for (int i = 0; i < n; i++) {
if (flg == 1)
break;
if (vis[i] != 1)
dfs(i);
}
if (flg == 1)
Console.Write("No" + "\n");
else
Console.Write("Yes" + "\n");
}
}
|
Javascript
<script>
let adj = new Array(100005);
let vis = new Array(100005);
let dist = new Array(100005);
for(let i = 0; i < 100005; i++)
{
vis[i] = 0;
dist[i] = 0;
}
let flg;
function dfs(curr)
{
vis[curr] = 1;
for(let i = 0; i < adj[curr].length; i++)
{
if (vis[adj[curr][i][0]] > 0)
{
if (dist[adj[curr][i][0]] !=
dist[curr] + adj[curr][i][1])
flg = 1;
}
else
{
dist[adj[curr][i][0]] = dist[curr] +
adj[curr][i][1];
dfs(adj[curr][i][0]);
}
}
}
let n = 4, m = 4;
flg = 0;
for(let i = 0; i < adj.length; i++)
{
adj[i] = [];
}
adj[0].push([1, 2]);
adj[1].push([0, -2]);
adj[1].push([2, 1]);
adj[2].push([1, -1]);
adj[2].push([3, -2]);
adj[3].push([2, 2]);
adj[3].push([0, -1]);
adj[0].push([3, 1]);
for(let i = 0; i < n; i++)
{
if (flg == 1)
break;
if (vis[i] != 1)
dfs(i);
}
if (flg == 1)
document.write("No" + "<br>");
else
document.write("Yes" + "<br>");
</script>
|
Time Complexity: O(V + E) where V is no of vertices and E is no of edges.
Space Complexity: O(V + E) where V is no of vertices and E is no of edges.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...