Count even paths in Binary Tree

Given a Binary Tree, the task is to count the number of even paths in the given Binary Tree. Even Path is a path where root to leaf path contains all even nodes only.

Examples:

Input: Below is the given Binary Tree: 

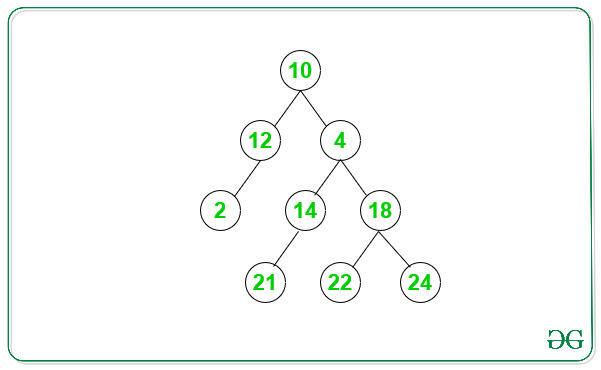
Output: 3 
Explanation:
There are 3 even path for the above Binary Tree: 
1. 10->12->2 
2. 10->4->18->22 
3. 10->4->18->24

Input: Below is the given Binary Tree: 

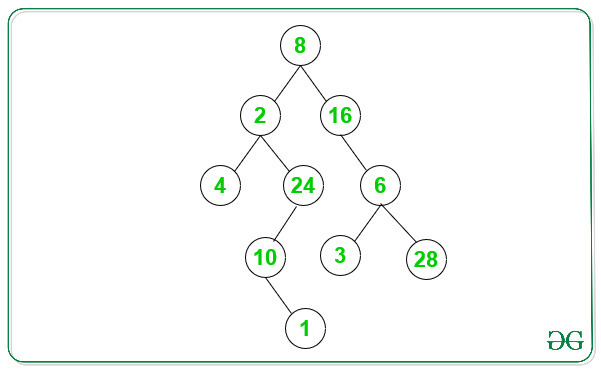
Output: 2 
Explanation:
There are 2 even path for the above Binary Tree: 
1. 8->2->4 
2. 8->16->6->28

Naive Approach: The idea is to generate all the root to leaf path and check whether all nodes in every path is even or not. Count all the paths with even nodes in it and return the count. The above implementation takes extra space to store the path.

Efficient Approach: The idea is to use Preorder Tree Traversal. During preorder traversal of the given binary tree do the following: 

1. If the current value of the node is odd or the pointer becomes NULL then return the count.
2. If the current node is a leaf node then increment the count by 1.
3. Recursively call for the left and right subtree with the updated count.
4. After the all-recursive calls, the value of count is the number of even paths for a given binary tree.

Below is the implementation of the above approach:  

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;

// A Tree node
struct Node {
    int key;
    struct Node *left, *right;
};

// Utility function to create a new node
Node* newNode(int key)
{
    Node* temp = new Node;
    temp->key = key;
    temp->left = temp->right = NULL;
    return (temp);
}

// Utility function to count the even path
// in a given Binary tree
int evenPaths(struct Node* node, int count)
{

    // Base Condition, when node pointer
    // becomes null or node value is odd
    if (node == NULL || (node->key % 2 != 0)) {
        return count;
    }

    // Increment count when encounter leaf
    // node with all node value even
    if (!node->left && !node->right) {
        count++;
    }

    // Left recursive call, and save the
    // value of count
    count = evenPaths(node->left, count);

    // Right recursive call, and return
    // value of count
    return evenPaths(node->right, count);
}

// Function to count the even paths in a
// given Binary tree
int countEvenPaths(struct Node* node)
{

    // Function call with count = 0
    return evenPaths(node, 0);
}

// Driver Code
int main()
{

    // Tree
    Node* root = newNode(12);
    root->left = newNode(13);
    root->right = newNode(12);

    root->right->left = newNode(14);
    root->right->right = newNode(16);

    root->right->left->left = newNode(21);
    root->right->left->right = newNode(22);
    root->right->right->left = newNode(22);
    root->right->right->right = newNode(24);
    root->right->right->right->left = newNode(8);

    // Function call
    cout << countEvenPaths(root);
    return 0;
}

Java

// Java program for the above approach
import java.util.*;
class GFG{

    // A Tree node
    static class Node {
        int key;
        Node left, right;
    };

    // Utility function to create a new node
    static Node newNode(int key)
    {
        Node temp = new Node();
        temp.key = key;
        temp.left = temp.right = null;
        return (temp);
    }

    // Utility function to count the even path
    // in a given Binary tree
    static int evenPaths(Node node, int count)
    {

        // Base Condition, when node pointer
        // becomes null or node value is odd
        if (node == null || (node.key % 2 != 0)) {
            return count;
        }

        // Increment count when encounter leaf
        // node with all node value even
        if (node.left == null && node.right == null) {
            count++;
        }

        // Left recursive call, and save the
        // value of count
        count = evenPaths(node.left, count);

        // Right recursive call, and return
        // value of count
        return evenPaths(node.right, count);
    }

    // Function to count the even paths in a
    // given Binary tree
    static int countEvenPaths(Node node)
    {

        // Function call with count = 0
        return evenPaths(node, 0);
    }

    // Driver Code
    public static void main(String args[])
    {

        // Tree
        Node root = newNode(12);
        root.left = newNode(13);
        root.right = newNode(12);

        root.right.left = newNode(14);
        root.right.right = newNode(16);

        root.right.left.left = newNode(21);
        root.right.left.right = newNode(22);
        root.right.right.left = newNode(22);
        root.right.right.right = newNode(24);
        root.right.right.right.left = newNode(8);

        // Function call
        System.out.println(countEvenPaths(root));

    }
}

// This code is contributed by AbhiThakur

Python3

# Python3 program for the
# above approach


# A Tree node
class Node:

    def __init__(self, x):

        self.key = x
        self.left = None
        self.right = None

# Utility function to count
# the even path in a given
# Binary tree
def evenPaths(node, count):

    # Base Condition, when node
    # pointer becomes null or
    # node value is odd
    if (node == None or
       (node.key % 2 != 0)):
        return count

    # Increment count when
    # encounter leaf node
    # with all node value even
    if (not node.left and
        not node.right):
        count+=1

    # Left recursive call, and
    # save the value of count
    count = evenPaths(node.left,
                      count)

    # Right recursive call, and
    # return value of count
    return evenPaths(node.right,
                     count)

# Function to count the even
# paths in a given Binary tree
def countEvenPaths(node):

    # Function call with count = 0
    return evenPaths(node, 0)

# Driver Code
if __name__ == '__main__':

    #Tree
    root = Node(12)
    root.left = Node(13)
    root.right = Node(12)

    root.right.left = Node(14)
    root.right.right = Node(16)

    root.right.left.left = Node(21)
    root.right.left.right = Node(22)
    root.right.right.left = Node(22)
    root.right.right.right = Node(24)
    root.right.right.right.left = Node(8)

    #Function call
    print(countEvenPaths(root))

# This code is contributed by Mohit Kumar 29

C#

// C# program for the above approach
using System;

class GFG{

    // A Tree node
    class Node {
        public int key;
        public Node left, right;
    };

    // Utility function to create a new node
    static Node newNode(int key)
    {
        Node temp = new Node();
        temp.key = key;
        temp.left = temp.right = null;
        return (temp);
    }

    // Utility function to count the even path
    // in a given Binary tree
    static int evenPaths(Node node, int count)
    {

        // Base Condition, when node pointer
        // becomes null or node value is odd
        if (node == null || (node.key % 2 != 0)) {
            return count;
        }

        // Increment count when encounter leaf
        // node with all node value even
        if (node.left == null && node.right == null) {
            count++;
        }

        // Left recursive call, and save the
        // value of count
        count = evenPaths(node.left, count);

        // Right recursive call, and return
        // value of count
        return evenPaths(node.right, count);
    }

    // Function to count the even paths in a
    // given Binary tree
    static int countEvenPaths(Node node)
    {

        // Function call with count = 0
        return evenPaths(node, 0);
    }

    // Driver Code
    public static void Main(String []args)
    {

        // Tree
        Node root = newNode(12);
        root.left = newNode(13);
        root.right = newNode(12);

        root.right.left = newNode(14);
        root.right.right = newNode(16);

        root.right.left.left = newNode(21);
        root.right.left.right = newNode(22);
        root.right.right.left = newNode(22);
        root.right.right.right = newNode(24);
        root.right.right.right.left = newNode(8);

        // Function call
        Console.WriteLine(countEvenPaths(root));

    }
}

// This code is contributed by PrinciRaj1992

Javascript

<script>

// Javascript program for the above approach

// A Tree node
class Node
{

    // Utility function to create
    // a new node
    constructor(key)
    {
        this.key = key;
        this.left = this.right = null;
    }
}

// Utility function to count the even path
// in a given Binary tree
function evenPaths(node, count)
{

    // Base Condition, when node pointer
    // becomes null or node value is odd
    if (node == null || (node.key % 2 != 0))
    {
        return count;
    }

    // Increment count when encounter leaf
    // node with all node value even
    if (node.left == null && node.right == null)
    {
        count++;
    }

    // Left recursive call, and save the
    // value of count
    count = evenPaths(node.left, count);

    // Right recursive call, and return
    // value of count
    return evenPaths(node.right, count);
}

// Function to count the even paths in a
// given Binary tree
function countEvenPaths(node)
{

    // Function call with count = 0
    return evenPaths(node, 0);
}

// Driver Code
let root = new Node(12);
root.left = new Node(13);
root.right = new Node(12);

root.right.left = new Node(14);
root.right.right = new Node(16);

root.right.left.left = new Node(21);
root.right.left.right = new Node(22);
root.right.right.left = new Node(22);
root.right.right.right = new Node(24);
root.right.right.right.left = new Node(8);

// Function call
document.write(countEvenPaths(root));

// This code is contributed by unknown2108

</script>

Output:

3

Time Complexity: O(N), where N is the number of nodes in the given binary tree.
Auxiliary Space: O(H), where H is the height of the binary tree. This is because the space used by the recursive call stack is proportional to the height of the tree. In the worst case scenario, when the tree is skewed and has a height of N (i.e., a linked list), the space complexity would be O(N).