Red Black Tree vs AVL Tree

In this post, we will compare Red-Black Tree and AVL Tree. 

Red Black Tree: 

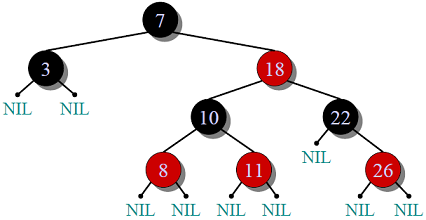
Properties:

1. Self-Balancing is provided by painting each node with two colors(Red or Black).
2. When the Tree is modified, a new tree is subsequently rearranged and repainted.
3. It requires 1 bit of color information for each node in the tree.
4. Time complexity: O(logn).

Constraints maintained by Red Black Tree:  

1. Root is always black.
2. All NULL leaves are black, and both children of a red node are black.
3. Every simple path from a given node to any of its descendant leaves contains the same number of black 
   nodes.
4. Path from root to farthest leaf is no more than twice as long as the path from the root to nearest leaf.
5. Time complexity: O(logn).

AVL(Adelson-Velskii and Landis) Tree

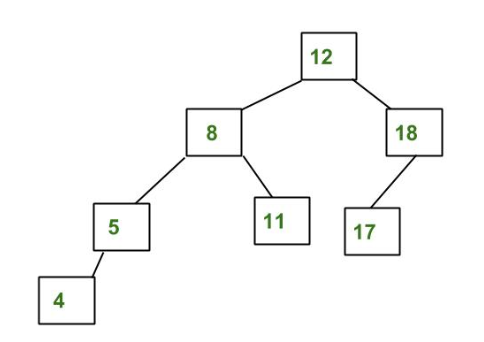
Properties:  

1. Height difference of the left and right subtree of the node should be less than 2.
2. Re-balancing is done when the heights of two child subtrees of a node differ by more than one.
3. Faster retrievals as strictly balanced.

Difference:

Basis of comparison	Red Black Trees	AVL Trees
Lookups	Red Black Trees has fewer lookups because they are not strictly balanced.	AVL trees provide faster lookups than Red-Black Trees because they are more strictly balanced.
Colour	In this, the color of the node is either Red or Black.	In this, there is no color of the node.
Insertion and removal	Red Black Trees provide faster insertion and removal operations than AVL trees as fewer rotations are done due to relatively relaxed balancing.	AVL trees provide complex insertion and removal operations as more rotations are done due to relatively strict balancing.
Storage	Red Black Tree requires only 1 bit of information per node.	AVL trees store balance factors or heights with each node thus requiring storage for an integer per node.
Searching	It does not provide efficient searching.	It provides efficient searching.
Uses	Red-Black Trees are used in most of the language libraries like map, multimap, multiset in C++, etc.	AVL trees are used in databases where faster retrievals are required.
Balance Factor	It does not gave balance factor	Each node has a balance factor whose value will be 1,0,-1
Balancing	Take less processing for balancing i.e.; maximum two rotation required	Take more processing for balancing