Combinatorial Game Theory | Set 3 (Grundy Numbers/Numbers and Mex)
Last Updated :
24 Aug, 2021
We have introduced Combinatorial Game Theory in Set 1 and discussed Game of Nim in Set 2.
Grundy Number is a number that defines a state of a game. We can define any impartial game (example : nim game) in terms of Grundy Number.
Grundy Numbers or Numbers determine how any Impartial Game (not only the Game of Nim) can be solved once we have calculated the Grundy Numbers associated with that game using Sprague-Grundy Theorem.
But before calculating Grundy Numbers, we need to learn about another term- Mex.
What is Mex?
‘Minimum excludant’ a.k.a ‘Mex’ of a set of numbers is the smallest non-negative number not present in the set.
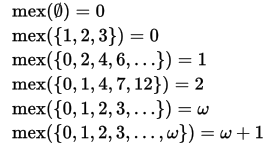
How to calculate Grundy Numbers?
We use this definition- The Grundy Number/ number is equal to 0 for a game that is lost immediately by the first player and is equal to Mex of the numbers of all possible next positions for any other game.
Below are three example games and programs to calculate Grundy Number and Mex for each of them. Calculation of Grundy Numbers is done basically by a recursive function called as calculateGrundy() function which uses calculateMex() function as its sub-routine.
Example 1
The game starts with a pile of n stones, and the player to move may take any positive number of stones. Calculate the Grundy Numbers for this game. The last player to move wins. Which player wins the game?
Since if the first player has 0 stones, he will lose immediately, so Grundy(0) = 0
If a player has 1 stones, then he can take all the stones and win. So the next possible position of the game (for the other player) is (0) stones
Hence, Grundy(1) = Mex(0) = 1 [According to the definition of Mex]
Similarly, If a player has 2 stones, then he can take only 1 stone or he can take all the stones and wins. So the next possible position of the game (for the other player) is (1, 0) stones respectively.
Hence, Grundy(2) = Mex(0, 1) = 2 [According to the definition of Mex]
Similarly, If a player has ‘n’ stones, then he can take only 1 stone, or he can take 2 stones…….. or he can take all the stones and win. So the next possible position of the game (for the other player) is (n-1, n-2,….1) stones respectively.
Hence, Grundy(n) = Mex (0, 1, 2, ….n-1) = n [According to the definition of Mex]
We summarize the first the Grundy Value from 0 to 10 in the below table-

C++
#include<bits/stdc++.h>
using namespace std;
int calculateMex(unordered_set<int> Set)
{
int Mex = 0;
while (Set.find(Mex) != Set.end())
Mex++;
return (Mex);
}
int calculateGrundy(int n)
{
if (n == 0)
return (0);
unordered_set<int> Set;
for (int i=0; i<=n-1; i++)
Set.insert(calculateGrundy(i));
return (calculateMex(Set));
}
int main()
{
int n = 10;
printf("%d", calculateGrundy(n));
return (0);
}
|
Java
import java.util.*;
class GFG{
public static int calculateMex(Set<Integer> Set)
{
int Mex = 0;
while (Set.contains(Mex))
Mex++;
return (Mex);
}
public static int calculateGrundy(int n)
{
if (n == 0)
return (0);
Set<Integer> Set = new HashSet<Integer>();
for(int i = 0; i <= n - 1; i++)
Set.add(calculateGrundy(i));
return (calculateMex(Set));
}
public static void main(String[] args)
{
int n = 10;
System.out.print(calculateGrundy(n));
}
}
|
Python3
def calculateMex(Set):
Mex = 0
while (Mex in Set):
Mex += 1
return (Mex)
def calculateGrundy( n):
if (n == 0):
return (0)
Set = set()
for i in range(n):
Set.add(calculateGrundy(i));
return (calculateMex(Set))
n = 10;
print(calculateGrundy(n))
|
C#
using System;
using System.Collections;
using System.Collections.Generic;
class GFG{
static int calculateMex(HashSet<int> Set)
{
int Mex = 0;
while (Set.Contains(Mex))
Mex++;
return (Mex);
}
static int calculateGrundy(int n)
{
if (n == 0)
return (0);
HashSet<int> Set = new HashSet<int>();
for(int i = 0; i <= n - 1; i++)
Set.Add(calculateGrundy(i));
return (calculateMex(Set));
}
public static void Main(string []arg)
{
int n = 10;
Console.Write(calculateGrundy(n));
}
}
|
Javascript
<script>
function calculateMex( Set) {
var Mex = 0;
while (Set.has(Mex))
Mex++;
return (Mex);
}
function calculateGrundy(n) {
if (n == 0)
return (0);
var set = new Set();
for (i = 0; i <= n - 1; i++)
set.add(calculateGrundy(i));
return (calculateMex(set));
}
var n = 10;
document.write(calculateGrundy(n));
</script>
|
Output :
10
The above solution can be optimized using Dynamic Programming as there are overlapping subproblems. The Dynamic programming based implementation can be found here.
Example 2
The game starts with a pile of n stones, and the player to move may take any positive number of stones up to 3 only. The last player to move wins. Which player wins the game? This game is 1 pile version of Nim.
Since if the first player has 0 stones, he will lose immediately, so Grundy(0) = 0
If a player has 1 stones, then he can take all the stones and win. So the next possible position of the game (for the other player) is (0) stones
Hence, Grundy(1) = Mex(0) = 1 [According to the definition of Mex]
Similarly, if a player has 2 stones, then he can take only 1 stone or he can take 2 stones and win. So the next possible position of the game (for the other player) is (1, 0) stones respectively.
Hence, Grundy(2) = Mex(0, 1) = 2 [According to the definition of Mex]
Similarly, Grundy(3) = Mex(0, 1, 2) = 3 [According to the definition of Mex]
But what about 4 stones ?
If a player has 4 stones, then he can take 1 stone or he can take 2 stones or 3 stones, but he can’t take 4 stones (see the constraints of the game). So the next possible position of the game (for the other player) is (3, 2, 1) stones respectively.
Hence, Grundy(4) = Mex (1, 2, 3) = 0 [According to the definition of Mex]
So we can define Grundy Number of any n >= 4 recursively as-
Grundy(n) = Mex[Grundy (n-1), Grundy (n-2), Grundy (n-3)]
We summarize the first the Grundy Value from 0 to 10 in the below table-

C++
#include<bits/stdc++.h>
using namespace std;
int calculateGrundy(int n)
{
if (n == 0)
return (0);
if (n == 1)
return (1);
if (n == 2)
return (2);
if (n == 3)
return (3);
else
return (n%(3+1));
}
int main()
{
int n = 10;
printf("%d", calculateGrundy(n));
return (0);
}
|
Java
import java.util.*;
class GFG
{
static int calculateGrundy(int n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
if (n == 2)
return 2;
if (n == 3)
return 3;
else
return (n%(3+1));
}
public static void main(String[] args)
{
int n = 10;
System.out.printf("%d", calculateGrundy(n));
}
}
|
Python3
def calculateGrundy(n):
if 0 <= n <= 3:
return n
else:
return (n%(3+1));
if __name__ == "__main__":
n = 10
print(calculateGrundy(n))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int calculateGrundy(int n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
if (n == 2)
return 2;
if (n == 3)
return 3;
else
return (n%(3+1));
}
public static void Main(String[] args)
{
int n = 10;
Console.Write(calculateGrundy(n));
}
}
|
Javascript
<script>
function calculateGrundy(n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
if (n == 2)
return 2;
if (n == 3)
return 3;
else
return (n % (3 + 1));
}
let n = 10;
document.write(calculateGrundy(n));
</script>
|
Output :
2
The general solution for above code when we are allowed to pick upto k stones can be found here.
Example 3
The game starts with a number- ‘n’ and the player to move divides the number- ‘n’ with 2, 3 or 6 and then takes the floor. If the integer becomes 0, it is removed. The last player to move wins. Which player wins the game?
We summarize the first the Grundy Value from 0 to 10 in the below table:

Think about how we generated this table.
C++
#include<bits/stdc++.h>
using namespace std;
int calculateMex(unordered_set<int> Set)
{
int Mex = 0;
while (Set.find(Mex) != Set.end())
Mex++;
return (Mex);
}
int calculateGrundy (int n)
{
if (n == 0)
return (0);
unordered_set<int> Set;
Set.insert(calculateGrundy(n/2));
Set.insert(calculateGrundy(n/3));
Set.insert(calculateGrundy(n/6));
return (calculateMex(Set));
}
int main()
{
int n = 10;
printf("%d", calculateGrundy (n));
return (0);
}
|
Java
import java.util.*;
class GFG
{
static int calculateMex(HashSet<Integer> Set)
{
int Mex = 0;
while (Set.contains(Mex))
{
Mex++;
}
return (Mex);
}
static int calculateGrundy(int n)
{
if (n == 0)
{
return (0);
}
HashSet<Integer> Set = new HashSet<Integer>();
Set.add(calculateGrundy(n / 2));
Set.add(calculateGrundy(n / 3));
Set.add(calculateGrundy(n / 6));
return (calculateMex(Set));
}
public static void main(String[] args)
{
int n = 10;
System.out.printf("%d", calculateGrundy(n));
}
}
|
Python3
def calculateMex(Set):
Mex = 0
while Mex in Set:
Mex += 1
return Mex
def calculateGrundy(n):
if n == 0:
return 0
Set = set()
Set.add(calculateGrundy(n // 2))
Set.add(calculateGrundy(n // 3))
Set.add(calculateGrundy(n // 6))
return (calculateMex(Set))
if __name__ == "__main__":
n = 10
print(calculateGrundy(n))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int calculateMex(HashSet<int> Set)
{
int Mex = 0;
while (Set.Contains(Mex))
{
Mex++;
}
return (Mex);
}
static int calculateGrundy(int n)
{
if (n == 0)
{
return (0);
}
HashSet<int> Set = new HashSet<int>();
Set.Add(calculateGrundy(n / 2));
Set.Add(calculateGrundy(n / 3));
Set.Add(calculateGrundy(n / 6));
return (calculateMex(Set));
}
public static void Main()
{
int n = 10;
Console.WriteLine(calculateGrundy(n));
}
}
|
Javascript
<script>
function calculateMex(set)
{
let Mex = 0;
while (set.has(Mex))
{
Mex++;
}
return (Mex);
}
function calculateGrundy(n)
{
if (n == 0)
{
return (0);
}
let set = new Set();
set.add(calculateGrundy(Math.floor(n / 2)));
set.add(calculateGrundy(Math.floor(n / 3)));
set.add(calculateGrundy(Math.floor(n / 6)));
return(calculateMex(set));
}
let n = 10;
document.write(calculateGrundy(n));
</script>
|
Output :
0
The above solution can be optimized using Dynamic Programming as there are overlapping subproblems. The Dynamic programming based implementation can be found here.
References-
https://en.wikipedia.org/wiki/Mex_(mathematics)
https://en.wikipedia.org/wiki/Number
In the next post, we will be discussing solutions to Impartial Games using Grundy Numbers or Numbers.
Share your thoughts in the comments
Please Login to comment...