Clustering/Partitioning an array such that sum of square differences is minimum
Last Updated :
14 Sep, 2023
Given an array of n numbers and a number k. We need to divide the array into k partitions (clusters) of the same or different lengths. For a given k, there can be one or more ways to make clusters (partitions). We define a function Cost(i) for the ith cluster, as the square of the difference between its first and last element. If the current cluster is

, where leni is the length of current cluster, then :
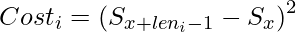
Amongst all the possible kinds of partitions, we have to find the partition that will minimize the function,
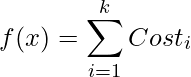
Examples :
Input : arr[] = {1, 5, 8, 10}
k = 2
Output : 20
Explanation :
Consider clustering 4 elements 1, 5, 8, 10
into 2 clusters. There are three options:
1. S1 = 1, S2 = 5, 8, 10, with total cost
02 + 52 = 25.
2. S1 = 1, 5, S2 = 8, 10, with total cost
42 + 22 = 20
3. S1 = 1, 5, 8, S2 = 10, with total cost
72 + 02 = 49
So, the optimal clustering is the second one,
so the output of the above problem is 20.
Input : arr[] = {5, 8, 1, 10}
k = 3
Output :
9
Explanation :
The three partitions are {5, 8}, {1} and {10}
To solve the problem, we assume that we have k slabs. We have to insert them in some k different positions in the array, which will give us the required partition scheme, and the one having a minimum value for f(x) will be the answer.
Naive solution: If we solve the above problem by the naive method, we would simply take all the possibilities and compute the minimum.
Implementation:
C++
#include<iostream>
using namespace std;
const int inf = 1000000000;
int ans = inf;
void solve(int i, int par, int a[], int n,
int k, int current_ans)
{
if (par > k)
return;
if (par==k && i==n-1)
{
ans = min(ans, current_ans);
return;
}
for (int j=i+1; j<n; j++)
solve(j, par+1, a, n, k, current_ans +
(a[j]-a[i+1])*(a[j]-a[i+1]));
}
int main()
{
int k = 2;
int a[] = {1, 5, 8, 10};
int n = sizeof(a)/sizeof(a[0]);
solve(-1, 0, a, n, k, 0);
cout << ans << endl;
return 0;
}
|
Java
import java.io.*;
class GFG
{
static int inf = 1000000000;
static int ans = inf;
static void solve(int i, int par, int a[], int n,
int k, int current_ans)
{
if (par > k)
return;
if (par == k && i == n - 1)
{
ans = Math.min(ans, current_ans);
return;
}
for (int j = i + 1; j < n; j++)
solve(j, par + 1, a, n, k, current_ans +
(a[j] - a[i + 1]) * (a[j] - a[i + 1]));
}
public static void main (String[] args)
{
int k = 2;
int a[] = {1, 5, 8, 10};
int n = a.length;
solve(-1, 0, a, n, k, 0);
System.out.println(ans);
}
}
|
Python3
inf = 1000000000
ans = inf
def solve(i, par, a, n, k, current_ans):
if (par > k):
return 0
global ans
if (par == k and i == n - 1):
ans = min(ans, current_ans)
return 0
for j in range(i + 1, n):
solve(j, par + 1, a, n, k, current_ans +
(a[j] - a[i + 1]) * (a[j] - a[i + 1]))
k = 2
a = [1, 5, 8, 10]
n = len(a)
solve(-1, 0, a, n, k, 0)
print(ans)
|
C#
using System;
class GFG
{
static int inf = 1000000000;
static int ans = inf;
static void solve(int i, int par, int []a,
int n, int k, int current_ans)
{
if (par > k)
return;
if (par == k && i == n - 1)
{
ans = Math.Min(ans, current_ans);
return;
}
for (int j = i + 1; j < n; j++)
solve(j, par + 1, a, n, k, current_ans +
(a[j] - a[i + 1]) * (a[j] - a[i + 1]));
}
public static void Main ()
{
int k = 2;
int []a = {1, 5, 8, 10};
int n = a.Length;
solve(-1, 0, a, n, k, 0);
Console.Write(ans);
}
}
|
PHP
<?php
$inf = 1000000000;
$ans = $inf;
function solve($i, $par, &$a, $n, $k, $current_ans)
{
global $inf, $ans;
if ($par > $k)
return;
if ($par == $k && $i == $n - 1)
{
$ans = min($ans, $current_ans);
return;
}
for ($j = $i + 1; $j < $n; $j++)
solve($j, $par + 1, $a, $n, $k, $current_ans +
($a[$j] - $a[$i + 1]) *
($a[$j] - $a[$i + 1]));
}
$k = 2;
$a = array(1, 5, 8, 10);
$n = sizeof($a);
solve(-1, 0, $a, $n, $k, 0);
echo $ans . "\n";
?>
|
Javascript
<script>
let inf = 1000000000;
let ans = inf;
function solve(i,par,a,n,k,current_ans)
{
if (par > k)
return;
if (par == k && i == n - 1)
{
ans = Math.min(ans, current_ans);
return;
}
for (let j = i + 1; j < n; j++)
solve(j, par + 1, a, n, k, current_ans +
(a[j] - a[i + 1]) * (a[j] - a[i + 1]));
}
let k = 2;
let a=[1, 5, 8, 10];
let n = a.length;
solve(-1, 0, a, n, k, 0);
document.write(ans);
</script>
|
Time Complexity: O(2n)
Space Complexity: O(n) where n is recursion stack space.
Dynamic Programming:
We create a table dp[n+1][k+1] table and initialize all values as infinite.
dp[i][j] stores optimal partition cost
for arr[0..i-1] and j partitions.
Let us compute the value of dp[i][j]. we take an index m, such that m < i, and put a partition next to that position such that there is no slab in between the indices i and m. It can be seen simply that answer to the current scenario is dp[m][j-1] + (a[i-1]-a[m])*(a[i-1]-a[m]), where the first term signifies the minimum f(x) till the mth element with j-1 partitions and the second one signifies the cost of current cluster. So we will take the minimum of all the possible indices m and dp[i][j] will be assigned the minimum amongst them.
Implementation:
C++
#include<iostream>
using namespace std;
const int inf = 1000000000;
int minCost(int a[], int n, int k)
{
int dp[n+1][k+1];
for (int i=0; i<=n; i++)
for (int j=0;j<=k;j++)
dp[i][j] = inf;
dp[0][0] = 0;
for (int i=1;i<=n;i++)
for (int j=1;j<=k;j++)
for (int m=i-1;m>=0;m--)
dp[i][j] = min(dp[i][j], dp[m][j-1] +
(a[i-1]-a[m])*(a[i-1]-a[m]));
return dp[n][k];
}
int main()
{
int k = 2;
int a[] = {1, 5, 8, 10};
int n = sizeof(a)/sizeof(a[0]);
cout << minCost(a, n, k) << endl;
return 0;
}
|
Java
import java.io.*;
class GFG
{
static int inf = 1000000000;
static int minCost(int a[], int n, int k)
{
int dp[][] = new int[n + 1][k + 1];
for (int i = 0; i <= n; i++)
for (int j = 0; j <= k; j++)
dp[i][j] = inf;
dp[0][0] = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= k; j++)
for (int m = i - 1; m >= 0; m--)
dp[i][j] = Math.min(dp[i][j], dp[m][j - 1] +
(a[i - 1] - a[m]) * (a[i - 1] - a[m]));
return dp[n][k];
}
public static void main (String[] args)
{
int k = 2;
int a[] = {1, 5, 8, 10};
int n = a.length;
System.out.println(minCost(a, n, k));
}
}
|
Python3
inf = 1000000000;
def minCost(a, n, k):
dp = [[inf for i in range(k + 1)]
for j in range(n + 1)];
dp[0][0] = 0;
for i in range(1, n + 1):
for j in range(1, k + 1):
for m in range(i - 1, -1, -1):
dp[i][j] = min(dp[i][j], dp[m][j - 1] +
(a[i - 1] - a[m]) *
(a[i - 1] - a[m]));
return dp[n][k];
if __name__ == '__main__':
k = 2;
a = [1, 5, 8, 10];
n = len(a);
print(minCost(a, n, k));
|
C#
using System;
class GFG {
static int inf = 1000000000;
static int minCost(int []a, int n, int k)
{
int [,]dp = new int[n + 1,k + 1];
for (int i = 0; i <= n; i++)
for (int j = 0; j <= k; j++)
dp[i,j] = inf;
dp[0,0] = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= k; j++)
for (int m = i - 1; m >= 0; m--)
dp[i,j] = Math.Min(dp[i,j],
dp[m,j - 1] +
(a[i - 1] - a[m]) *
(a[i - 1] - a[m]));
return dp[n,k];
}
public static void Main ()
{
int k = 2;
int []a = {1, 5, 8, 10};
int n = a.Length;
Console.Write(minCost(a, n, k));
}
}
|
Javascript
<script>
let inf = 1000000000;
function minCost(a, n, k)
{
let dp = new Array(n + 1);
for (let i = 0; i <= n; i++)
{
dp[i] = new Array(k + 1);
for (let j = 0; j <= k; j++)
dp[i][j] = inf;
}
dp[0][0] = 0;
for (let i = 1; i <= n; i++)
for (let j = 1; j <= k; j++)
for (let m = i - 1; m >= 0; m--)
dp[i][j] = Math.min(dp[i][j], dp[m][j - 1] +
(a[i - 1] - a[m]) * (a[i - 1] - a[m]));
return dp[n][k];
}
let k = 2;
let a = [1, 5, 8, 10];
let n = a.length;
document.write(minCost(a, n, k));
</script>
|
Time Complexity: O(k * n2)
Auxiliary Space: O(n*k)
This article is contributed by Amritya Vagmi and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org.
Share your thoughts in the comments
Please Login to comment...