Class 11 NCERT Solutions- Chapter 3 Trigonometric Function – Exercise 3.3 | Set 1
Last Updated :
16 Apr, 2021
Prove that:
Question 1: sin2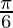 +cos2
+cos2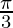 – tan2
– tan2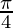 =
=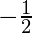
Solution:
Taking LHS in consideration, we get
= sin2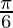 +cos2
+cos2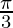 – tan2
– tan2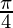
Substituting the values,
=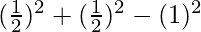
= – 1
– 1
=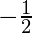
Hence, LHS = RHS
Question 2: 2sin2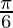 +cosec2
+cosec2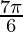 cos2
cos2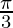 =
=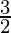
Solution:
Taking LHS in consideration, we get
= 2sin2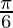 +cosec2
+cosec2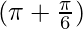 cos2
cos2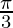
= 2sin2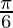 + (- cosec
+ (- cosec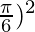 cos2
cos2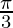
Substituting the values,
=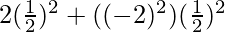
= 2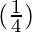 + 4
+ 4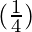
= + 1
+ 1
=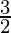
Hence, LHS = RHS
Question 3: cot2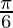 + cosec
+ cosec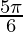 + 3tan2
+ 3tan2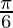 = 6
= 6
Solution:
Taking LHS in consideration, we get
= cot2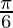 + cosec
+ cosec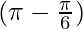 + 3tan2
+ 3tan2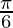
= cot2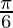 + cosec
+ cosec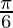 + 3tan2
+ 3tan2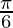
Substituting the values,
= (√3)2 + 2 + 3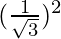
= 3 + 2 + 3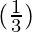
= 6
Hence, LHS = RHS
Question 4: 2sin2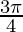 + 2cos2
+ 2cos2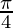 + 2sec2
+ 2sec2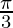 = 10
= 10
Solution:
Taking LHS in consideration, we get
= 2sin2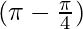 + 2cos2
+ 2cos2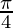 + 2sec2
+ 2sec2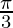
= 2sin2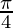 + 2cos2
+ 2cos2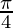 + 2sec2
+ 2sec2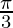
Substituting the values,
=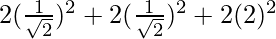
= 2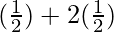 + 2(4)
+ 2(4)
= 1 + 1 + 8
= 10
Hence, LHS = RHS
Question 5: Find the value of:
(i) sin 75°
Solution:
As, we don’t know the angle value for 75°, so we will break into the angles which we know.
75° = 30° + 45°, so lets use this and solve for sin(30° + 45°)
Using the trigonometric formula,
sin (A+B) = sin A cos B + cos A sin B
sin(30° + 45°) = sin 30° cos 45° + cos 30° sin 45°
Substituting values, we get
sin(75°) =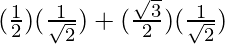
sin(75°) =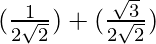
sin(75°) =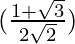
(ii) tan 15°
Solution:
As, we don’t know the angle value for 15°, so we will break into the angles which we know.
15° = 60° – 45° or 45° – 30° so lets use this and solve for tan(45° – 30°)
Using the trigonometric formula,
tan (A-B) =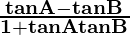
tan(45° – 30°) =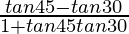
Substituting values, we get
tan(15°) =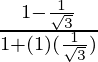
tan(15°) =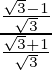
tan(15°) =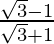
Now rationalizing the denominator, multiply and divide by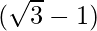
tan(15°) =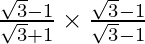
tan(15°) =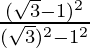
tan(15°) =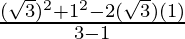
tan(15°) =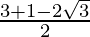
tan(15°) =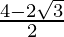
tan(15°) = 2 –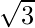
Prove the following:
Question 6: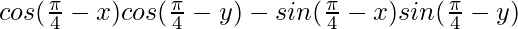 = sin (x+y)
= sin (x+y)
Solution:
Taking LHS in consideration, we get
=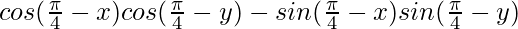
As, here there is multiplication of cos cos and sin sin, we will use Defactorisation Formulae,
2 cos A cos B = cos (A+B) + cos (A-B) and, ……………….(1)
2 sin A sin B = cos (A-B) – cos (A+B) ……………….(2)
Multiply and divide LHS by 2, we get
=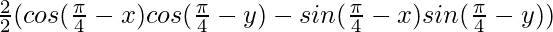
=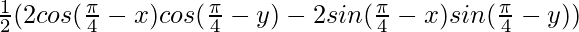
Subtracting (2) from (1) and using identity formulae, we get
2 cos A cos B – 2 sin A sin B = cos (A+B) + cos (A-B) – (cos (A-B) – cos (A+B))
2 cos A cos B – 2 sin A sin B = 2 cos (A+B)
Hence, using this
=![Rendered by QuickLaTeX.com \frac{1}{2}[2 cos ((\frac{\pi}{4}-x)+ (\frac{\pi}{4}-y))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-584094cdd1dd40d757104a005da5e0a6_l3.png)
= cos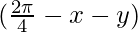
= cos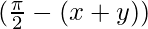
= sin (x+y) (As cos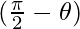 = sin θ)
= sin θ)
Hence, LHS = RHS
Question 7: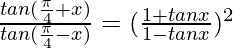
Solution:
Taking LHS in consideration, we get
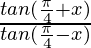
As, using Factorisation Formulae of tan, we have
tan (A+B) =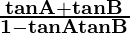 and,
and,
tan (A-B) =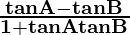
Now, substituting the values
=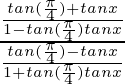
=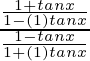
=
=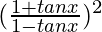
Hence, LHS = RHS
Question 8: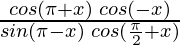 = cot2x
= cot2x
Solution:
Taking LHS in consideration, we get
=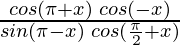
As, we know these standard values
cos(-x) = cos x
cos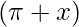 = – cos x
= – cos x
sin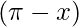 = sin x
= sin x
cos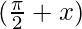 = – sin x
= – sin x
Substituting these values, we have
=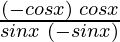
=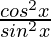
= cot2 x
Hence, LHS = RHS
Question 9:![Rendered by QuickLaTeX.com cos (\frac{3\pi}{2}+x)\hspace{0.1cm}cos (2\pi+x)[\hspace{0.1cm}cot (\frac{3\pi}{2}-x)+cot(2\pi+x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d43435004ad57d6f47e9e18c75e691b_l3.png) = 1
= 1
Solution:
Taking LHS in consideration, we get
=![Rendered by QuickLaTeX.com cos (\frac{3\pi}{2}+x)\hspace{0.1cm}cos (2\pi+x)[\hspace{0.1cm}cot (\frac{3\pi}{2}-x)+cot(2\pi+x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-013e0a0e1435e12ab0987420920b9b1d_l3.png)
As, we know these standard values
cos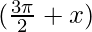 = sin x
= sin x
cos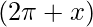 = cos x
= cos x
cot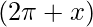 = cot x
= cot x
cot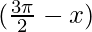 = tan x
= tan x
Substituting the values, we have
=![Rendered by QuickLaTeX.com sin x\hspace{0.1cm}cos x[\hspace{0.1cm}tan x + cot x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ddc63015776a5a5a633150ecb238e3bc_l3.png)
=![Rendered by QuickLaTeX.com sin x\hspace{0.1cm}cos x[\frac{sin x}{cos x} + \frac{cos x}{sin x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-be4aa9775ddbe250c52332d3eba6b4a2_l3.png)
=![Rendered by QuickLaTeX.com sin x\hspace{0.1cm}cos x[\frac{sin^2 x + cos^2 x}{sin x \hspace{0.1cm}cos x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f2622ad362d7cb26ad1eef4055f3e75a_l3.png)
As sin2 x + cos2 x = 1
= 1
Hence, LHS = RHS
Question 10: sin(n + 1)x sin(n + 2)x + cos(n + 1)x cos(n + 2)x = cos x
Solution:
Taking LHS in consideration, we get
= sin(n + 1)x sin(n + 2)x + cos(n + 1)x cos(n + 2)x
As, here there is multiplication of cos cos and sin sin, we will use Defactorisation Formulae,
2 cos A cos B = cos (A+B) + cos (A-B) and, ……………….(1)
2 sin A sin B = cos (A-B) – cos (A+B) ……………….(2)
Multiply and divide LHS by 2, we get
=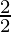 (sin(n + 1)x sin(n + 2)x + cos(n + 1)x cos(n + 2)x)
(sin(n + 1)x sin(n + 2)x + cos(n + 1)x cos(n + 2)x)
= (2 sin(n + 1)x sin(n + 2)x + 2 cos(n + 1)x cos(n + 2)x)
(2 sin(n + 1)x sin(n + 2)x + 2 cos(n + 1)x cos(n + 2)x)
Adding (1) and (2) and using identity formulae, we get
2 cos A cos B + 2 sin A sin B = cos (A+B) + cos (A-B) + cos (A-B) – cos (A+B)
2 cos A cos B + 2 sin A sin B = 2 cos (A-B)
Hence, using this
= (2 cos((n + 1)x – (n + 2)x))
(2 cos((n + 1)x – (n + 2)x))
= cos((n + 1)x – (n + 2)x)
= cos (x-2x)
= cos (- x)
= cos x (As, cos(-x) = cos x)
Hence, LHS = RHS
Question 11: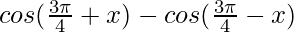 = –
= –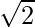 sin x
sin x
Solution:
Taking LHS in consideration, we get
=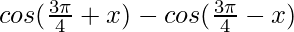
Using the identity,
cos A – cos B = 2 sin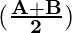 sin
sin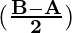
Substituting the values,
=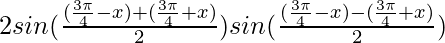
= 2 sin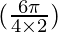 sin
sin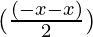
= 2 sin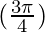 sin (-x)
sin (-x)
= 2 sin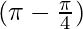 sin (-x)
sin (-x)
= 2 ( sin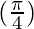 ) sin (-x)
) sin (-x)
= 2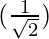 (- sin x)
(- sin x)
=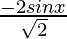
Rationalizing the denominator, by multiplying and dividing by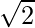
=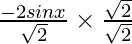
=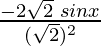
=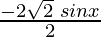
=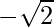 sin x
sin x
Hence, LHS = RHS
Question 12: sin2 6x – sin2 4x = sin 2x sin 10x
Solution:
Taking LHS in consideration, we get
= sin2 6x – sin2 4x
= sin 6x sin 6x – sin 4x sin 4x
As, here there is multiplication of sin sin, we will use Defactorisation Formulae,
2 sin A sin B = cos (A-B) – cos (A+B)
Multiply and divide LHS by 2, we get
=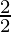 (sin 6x sin 6x – sin 4x sin 4x)
(sin 6x sin 6x – sin 4x sin 4x)
= (2 sin 6x sin 6x – 2 sin 4x sin 4x)
(2 sin 6x sin 6x – 2 sin 4x sin 4x)
Using the identity, we can simplify
= [(cos(6x-6x) – cos(6x+6x)) – (cos(4x-4x) – cos(4x+4x))]
[(cos(6x-6x) – cos(6x+6x)) – (cos(4x-4x) – cos(4x+4x))]
= [(cos(0) – cos(12x)) – (cos(0) – cos(8x))]
[(cos(0) – cos(12x)) – (cos(0) – cos(8x))]
= [1 – cos(12x) – 1 + cos(8x)] (As, cos 0 = 1)
[1 – cos(12x) – 1 + cos(8x)] (As, cos 0 = 1)
= [cos(8x) – cos (12x)]
[cos(8x) – cos (12x)]
Now, using the identity
cos A – cos B = 2 sin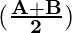 sin
sin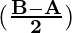
Substituting the values, we have
=![Rendered by QuickLaTeX.com \frac{1}{2}[2 \hspace{0.1cm}sin (\frac{8x+12x}{2}) \hspace{0.1cm}sin (\frac{12x-8x}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6f7084eafaf9c575bbd9240d7abae9a6_l3.png)
= sin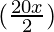 sin
sin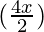
= sin (10 x) sin (2x)
Hence, LHS = RHS
Question 13: cos2 2x – cos2 6x = sin 4x sin 8x
Solution:
Taking LHS in consideration, we get
= cos2 2x – cos2 6x
= cos 2x cos 2x – cos 6x cos 6x
As, here there is multiplication of cos cos, we will use Defactorisation Formulae,
2 cos A cos B = cos (A+B) + cos (A-B)
Multiply and divide LHS by 2, we get
=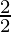 (cos 2x cos 2x – cos 6x cos 6x)
(cos 2x cos 2x – cos 6x cos 6x)
= (2 cos 2x cos 2x – 2 cos 6x cos 6x)
(2 cos 2x cos 2x – 2 cos 6x cos 6x)
Using the identity, we can simplify
= [(cos(2x+2x) + cos(2x-2x)) – (cos(6x+6x) + cos(6x-6x))]
[(cos(2x+2x) + cos(2x-2x)) – (cos(6x+6x) + cos(6x-6x))]
= [(cos(2x+2x) + cos(0)) – (cos(6x+6x) + cos(0))]
[(cos(2x+2x) + cos(0)) – (cos(6x+6x) + cos(0))]
= [(cos(4x) + 1 – cos(12x) – 1)] (As, cos 0 = 1)
[(cos(4x) + 1 – cos(12x) – 1)] (As, cos 0 = 1)
= [cos(4x) – cos(12x)]
[cos(4x) – cos(12x)]
Now, using the identity
cos A – cos B = 2 sin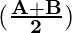 sin
sin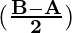
Substituting the values, we have
=![Rendered by QuickLaTeX.com \frac{1}{2}[2 \hspace{0.1cm}sin (\frac{4x+12x}{2}) \hspace{0.1cm}sin (\frac{12x-4x}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fe6218cb12be274057abea3b737459be_l3.png)
= sin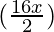 sin
sin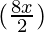
= sin (8x) sin (4x)
Hence, LHS = RHS
Question 14: sin 2x + 2 sin 4x + sin 6x = 4 cos2 x sin 4x
Solution:
Taking LHS in consideration, we get
sin 2x + 2 sin 4x + sin 6x
After rearranging, we have
= (sin 2x + sin 6x) + 2 sin 4x
Using the identity, we can simplify
sin A+ sin B = 2 sin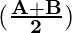 cos
cos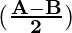
= 2 sin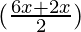 cos
cos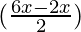 + 2 sin 4x
+ 2 sin 4x
= 2 sin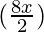 cos
cos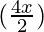 + 2 sin 4x
+ 2 sin 4x
= 2 sin (4x) cos (2x) + 2 sin 4x
Taking (2 sin 4x), we have
= 2 sin (4x) (cos (2x) + 1)
= 2 sin (4x) (2 cos2 x – 1 + 1) (As, cos 2θ = 2cos2 θ – 1)
= 2 sin (4x) (2 cos2 x)
= 4 sin (4x) cos2 x
Hence, LHS = RHS
Share your thoughts in the comments
Please Login to comment...