Check sum of Covered and Uncovered nodes of Binary Tree
Last Updated :
20 Feb, 2023
Given a binary tree, you need to check whether sum of all covered elements is equal to sum of all uncovered elements or not.
In a binary tree, a node is called Uncovered if it appears either on left boundary or right boundary. Rest of the nodes are called covered.
For example, consider below binary tree
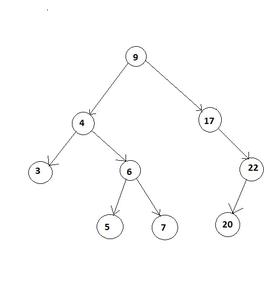
Binary Tree with covered and uncovered Nodes
In above binary tree,
Covered node: 6, 5, 7
Uncovered node: 9, 4, 3, 17, 22, 20
The output for this tree should be false as
sum of covered and uncovered node is not same
We strongly recommend you to minimize your browser and try this yourself first.
For calculating sum of Uncovered nodes we will follow below steps:
1) Start from root, go to left and keep going until left child is available, if not go to right child and again follow same procedure until you reach a leaf node.
2) After step 1 sum of left boundary will be stored, now for right part again do the same procedure but now keep going to right until right child is available, if not then go to left child and follow same procedure until you reach a leaf node.
After above 2 steps sum of all Uncovered node will be stored, we can subtract it from total sum and get sum of covered elements and check for equines of binary tree.
C++
#include <bits/stdc++.h>
using namespace std;
struct Node
{
int key;
struct Node* left, *right;
};
struct Node* newNode(int key)
{
Node* temp = new Node;
temp->key = key;
temp->left = temp->right = NULL;
return (temp);
}
int sum(Node* t)
{
if (t == NULL)
return 0;
return t->key + sum(t->left) + sum(t->right);
}
int uncoveredSumLeft(Node* t)
{
if (t->left == NULL && t->right == NULL)
return t->key;
if (t->left != NULL)
return t->key + uncoveredSumLeft(t->left);
else
return t->key + uncoveredSumLeft(t->right);
}
int uncoveredSumRight(Node* t)
{
if (t->left == NULL && t->right == NULL)
return t->key;
if (t->right != NULL)
return t->key + uncoveredSumRight(t->right);
else
return t->key + uncoveredSumRight(t->left);
}
int uncoverSum(Node* t)
{
int lb = 0, rb = 0;
if (t->left != NULL)
lb = uncoveredSumLeft(t->left);
if (t->right != NULL)
rb = uncoveredSumRight(t->right);
return t->key + lb + rb;
}
bool isSumSame(Node *root)
{
int sumUC = uncoverSum(root);
int sumT = sum(root);
return (sumUC == (sumT - sumUC));
}
void inorder(Node* root)
{
if (root)
{
inorder(root->left);
printf("%d ", root->key);
inorder(root->right);
}
}
int main()
{
Node* root = newNode(8);
root->left = newNode(3);
root->left->left = newNode(1);
root->left->right = newNode(6);
root->left->right->left = newNode(4);
root->left->right->right = newNode(7);
root->right = newNode(10);
root->right->right = newNode(14);
root->right->right->left = newNode(13);
if (isSumSame(root))
printf("Sum of covered and uncovered is same\n");
else
printf("Sum of covered and uncovered is not same\n");
}
|
Java
class Node
{
int key;
Node left, right;
public Node(int key)
{
this.key = key;
left = right = null;
}
}
class BinaryTree
{
Node root;
int sum(Node t)
{
if (t == null)
return 0;
return t.key + sum(t.left) + sum(t.right);
}
int uncoveredSumLeft(Node t)
{
if (t.left == null && t.right == null)
return t.key;
if (t.left != null)
return t.key + uncoveredSumLeft(t.left);
else
return t.key + uncoveredSumLeft(t.right);
}
int uncoveredSumRight(Node t)
{
if (t.left == null && t.right == null)
return t.key;
if (t.right != null)
return t.key + uncoveredSumRight(t.right);
else
return t.key + uncoveredSumRight(t.left);
}
int uncoverSum(Node t)
{
int lb = 0, rb = 0;
if (t.left != null)
lb = uncoveredSumLeft(t.left);
if (t.right != null)
rb = uncoveredSumRight(t.right);
return t.key + lb + rb;
}
boolean isSumSame(Node root)
{
int sumUC = uncoverSum(root);
int sumT = sum(root);
return (sumUC == (sumT - sumUC));
}
void inorder(Node root)
{
if (root != null)
{
inorder(root.left);
System.out.print(root.key + " ");
inorder(root.right);
}
}
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(8);
tree.root.left = new Node(3);
tree.root.left.left = new Node(1);
tree.root.left.right = new Node(6);
tree.root.left.right.left = new Node(4);
tree.root.left.right.right = new Node(7);
tree.root.right = new Node(10);
tree.root.right.right = new Node(14);
tree.root.right.right.left = new Node(13);
if (tree.isSumSame(tree.root))
System.out.println("Sum of covered and uncovered is same");
else
System.out.println("Sum of covered and uncovered is not same");
}
}
|
Python3
class newNode:
def __init__(self, key):
self.key = key
self.left = self.right = None
def Sum(t):
if (t == None):
return 0
return t.key + Sum(t.left) + Sum(t.right)
def uncoveredSumLeft(t):
if (t.left == None and t.right == None):
return t.key
if (t.left != None):
return t.key + uncoveredSumLeft(t.left)
else:
return t.key + uncoveredSumLeft(t.right)
def uncoveredSumRight(t):
if (t.left == None and t.right == None):
return t.key
if (t.right != None):
return t.key + uncoveredSumRight(t.right)
else:
return t.key + uncoveredSumRight(t.left)
def uncoverSum(t):
lb = 0
rb = 0
if (t.left != None):
lb = uncoveredSumLeft(t.left)
if (t.right != None):
rb = uncoveredSumRight(t.right)
return t.key + lb + rb
def isSumSame(root):
sumUC = uncoverSum(root)
sumT = Sum(root)
return (sumUC == (sumT - sumUC))
def inorder(root):
if (root):
inorder(root.left)
print(root.key, end = " ")
inorder(root.right)
if __name__ == '__main__':
root = newNode(8)
root.left = newNode(3)
root.left.left = newNode(1)
root.left.right = newNode(6)
root.left.right.left = newNode(4)
root.left.right.right = newNode(7)
root.right = newNode(10)
root.right.right = newNode(14)
root.right.right.left = newNode(13)
if (isSumSame(root)):
print("Sum of covered and uncovered is same")
else:
print("Sum of covered and uncovered is not same")
|
C#
using System;
public class Node
{
public int key;
public Node left, right;
public Node(int key)
{
this.key = key;
left = right = null;
}
}
class GFG
{
public Node root;
public virtual int sum(Node t)
{
if (t == null)
{
return 0;
}
return t.key + sum(t.left) +
sum(t.right);
}
public virtual int uncoveredSumLeft(Node t)
{
if (t.left == null && t.right == null)
{
return t.key;
}
if (t.left != null)
{
return t.key + uncoveredSumLeft(t.left);
}
else
{
return t.key + uncoveredSumLeft(t.right);
}
}
public virtual int uncoveredSumRight(Node t)
{
if (t.left == null && t.right == null)
{
return t.key;
}
if (t.right != null)
{
return t.key + uncoveredSumRight(t.right);
}
else
{
return t.key + uncoveredSumRight(t.left);
}
}
public virtual int uncoverSum(Node t)
{
int lb = 0, rb = 0;
if (t.left != null)
{
lb = uncoveredSumLeft(t.left);
}
if (t.right != null)
{
rb = uncoveredSumRight(t.right);
}
return t.key + lb + rb;
}
public virtual bool isSumSame(Node root)
{
int sumUC = uncoverSum(root);
int sumT = sum(root);
return (sumUC == (sumT - sumUC));
}
public virtual void inorder(Node root)
{
if (root != null)
{
inorder(root.left);
Console.Write(root.key + " ");
inorder(root.right);
}
}
public static void Main(string[] args)
{
GFG tree = new GFG();
tree.root = new Node(8);
tree.root.left = new Node(3);
tree.root.left.left = new Node(1);
tree.root.left.right = new Node(6);
tree.root.left.right.left = new Node(4);
tree.root.left.right.right = new Node(7);
tree.root.right = new Node(10);
tree.root.right.right = new Node(14);
tree.root.right.right.left = new Node(13);
if (tree.isSumSame(tree.root))
{
Console.WriteLine("Sum of covered and " +
"uncovered is same");
}
else
{
Console.WriteLine("Sum of covered and " +
"uncovered is not same");
}
}
}
|
Javascript
<script>
class Node
{
constructor(key)
{
this.key = key;
this.left= null;
this.right = null;
}
}
var root = null;
function sum(t)
{
if (t == null)
{
return 0;
}
return t.key + sum(t.left) +
sum(t.right);
}
function uncoveredSumLeft(t)
{
if (t.left == null && t.right == null)
{
return t.key;
}
if (t.left != null)
{
return t.key + uncoveredSumLeft(t.left);
}
else
{
return t.key + uncoveredSumLeft(t.right);
}
}
function uncoveredSumRight(t)
{
if (t.left == null && t.right == null)
{
return t.key;
}
if (t.right != null)
{
return t.key + uncoveredSumRight(t.right);
}
else
{
return t.key + uncoveredSumRight(t.left);
}
}
function uncoverSum(t)
{
var lb = 0, rb = 0;
if (t.left != null)
{
lb = uncoveredSumLeft(t.left);
}
if (t.right != null)
{
rb = uncoveredSumRight(t.right);
}
return t.key + lb + rb;
}
function isSumSame(root)
{
var sumUC = uncoverSum(root);
var sumT = sum(root);
return (sumUC == (sumT - sumUC));
}
function inorder(root)
{
if (root != null)
{
inorder(root.left);
document.write(root.key + " ");
inorder(root.right);
}
}
var root = new Node(8);
root.left = new Node(3);
root.left.left = new Node(1);
root.left.right = new Node(6);
root.left.right.left = new Node(4);
root.left.right.right = new Node(7);
root.right = new Node(10);
root.right.right = new Node(14);
root.right.right.left = new Node(13);
if (isSumSame(root))
{
document.write("Sum of covered and " +
"uncovered is same");
}
else
{
document.write("Sum of covered and " +
"uncovered is not same");
}
</script>
|
Output :
Sum of covered and uncovered is not same
Time Complexity: O(N), node will run for every new node.
Space Complexity: O(N), space is needed for every node.
Share your thoughts in the comments
Please Login to comment...