Check if there exists a number with X factors out of which exactly K are prime
Last Updated :
20 Sep, 2023
Given two integers X and K, the task is to determine whether there exists a number that has exactly X factors out of which K is prime.
Examples:
Input: X = 8, K = 1
Output: Yes
Explanation:
The number is 128
Factors of 128 = {1, 2, 4, 8, 16, 32, 64, 128} which are 8 in count = X
Among these, only 2 is prime. Therefore count of prime factor = 1 = K
Input: X = 4, K = 2
Output: Yes
Explanation:
The number is 6
Factors of 6 = {1, 2, 3, 6} which are 4 in count = X
Among these, only 2 and 3 are prime. Therefore count of prime factor = 2 = K
Approach:
- Suppose a number N has X factors out of which K are prime, say
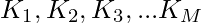
- Thus, number can be written as
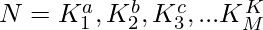 where, the total number of factors is calculated by
where, the total number of factors is calculated by 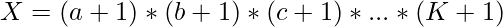
- It is observed that X is a product of “power+1” of the prime factors of the number. Thus, if we are able to divide X into a product of K numbers, then we can form a number with exactly X factors out of which K is prime.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool check(int X, int K)
{
int prime, temp, sqr, i;
prime = 0;
temp = X;
sqr = sqrt(X);
for (i = 2; i <= sqr; i++) {
while (temp % i == 0) {
temp = temp / i;
prime++;
}
}
if (temp > 2)
prime++;
if (X == 1)
return false;
if (prime == 1 && K == 1)
return true;
else if (prime >= K)
return true;
else
return false;
}
int main()
{
int X, K;
X = 4;
K = 2;
if (check(X, K))
cout << "Yes";
else
cout << "No";
}
|
Java
import java.util.*;
class GFG{
static boolean check(int X, int K)
{
int prime, temp, sqr, i;
prime = 0;
temp = X;
sqr = (int) Math.sqrt(X);
for (i = 2; i <= sqr; i++) {
while (temp % i == 0) {
temp = temp / i;
prime++;
}
}
if (temp > 2)
prime++;
if (X == 1)
return false;
if (prime == 1 && K == 1)
return true;
else if (prime >= K)
return true;
else
return false;
}
public static void main(String[] args)
{
int X, K;
X = 4;
K = 2;
if (check(X, K))
System.out.print("Yes");
else
System.out.print("No");
}
}
|
Python3
from math import sqrt
def check(X,K):
prime = 0
temp = X
sqr = int(sqrt(X))
for i in range(2,sqr+1,1):
while (temp % i == 0):
temp = temp // i
prime += 1
if (temp > 2):
prime += 1
if (X == 1):
return False
if (prime == 1 and K == 1):
return True
elif(prime >= K):
return True
else:
return False
if __name__ == '__main__':
X = 4
K = 2
if (check(X, K)):
print("Yes")
else:
print("No")
|
C#
using System;
class GFG{
static bool check(int X, int K)
{
int prime, temp, sqr, i;
prime = 0;
temp = X;
sqr = Convert.ToInt32(Math.Sqrt(X));
for (i = 2; i <= sqr; i++) {
while (temp % i == 0) {
temp = temp / i;
prime++;
}
}
if (temp > 2)
prime++;
if (X == 1)
return false;
if (prime == 1 && K == 1)
return true;
else if (prime >= K)
return true;
else
return false;
}
static public void Main ()
{
int X, K;
X = 4;
K = 2;
if (check(X, K))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Javascript
<script>
function check(X , K) {
var prime, temp, sqr, i;
prime = 0;
temp = X;
sqr = parseInt( Math.sqrt(X));
for (i = 2; i <= sqr; i++) {
while (temp % i == 0) {
temp = parseInt(temp / i);
prime++;
}
}
if (temp > 2)
prime++;
if (X == 1)
return false;
if (prime == 1 && K == 1)
return true;
else if (prime >= K)
return true;
else
return false;
}
var X, K;
X = 4;
K = 2;
if (check(X, K))
document.write("Yes");
else
document.write("No");
</script>
|
Time Complexity: O(sqrt(n) * log n)
Auxiliary Space: O(1)
Approach 2: Dynamic Programming:
- A dynamic programming approach to solve this problem involves the use of a two-dimensional array dp, where dp[i][j] represents the number of ways to form a number with i factors and j prime factors.
- The base cases are dp[1][0] = 1 and dp[1][1] = 0, since the only number with 1 factor is 1 and it has no prime factors. For i > 1 and j > 0, the recurrence relation is:
- dp[i][j] = dp[i-1][j] + dp[i-1][j-1]*p(i)
- where p(i) is the number of prime factors of i.
- The first term dp[i-1][j] represents the number of ways to form a number with i-1 factors and j prime factors, without including the factor i. The second term dp[i-1][j-1]*p(i) represents the number of ways to form a number with i-1 factors and j-1 prime factors, including the factor i.
- The final answer is the sum of dp[X][k] for all k from 1 to K, since we want to find if there exists a number with X factors and K prime factors.
Here’s the dynamic programming approach in code:
C++
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1005;
int dp[MAXN][MAXN];
int num_primes(int n) {
int cnt = 0;
for (int i = 2; i*i <= n; i++) {
while (n % i == 0) {
cnt++;
n /= i;
}
}
if (n > 1) cnt++;
return cnt;
}
bool check(int X, int K) {
memset(dp, 0, sizeof(dp));
dp[1][0] = 1;
for (int i = 2; i <= X; i++) {
for (int j = 1; j <= K; j++) {
dp[i][j] = dp[i-1][j] + dp[i-1][j-1]*num_primes(i);
}
}
for (int j = 1; j <= K; j++) {
if (dp[X][j] > 0) return true;
}
return false;
}
int main() {
int X = 4, K = 2;
if (check(X, K)) cout << "Yes\n";
else cout << "No\n";
return 0;
}
|
Java
import java.util.Scanner;
public class GFG {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int X = 4;
int K = 2;
if (check(X, K)) {
System.out.println("Yes");
} else {
System.out.println("No");
}
}
static int numPrimes(int n) {
int cnt = 0;
for (int i = 2; i <= Math.sqrt(n); i++) {
while (n % i == 0) {
cnt++;
n /= i;
}
}
if (n > 1) {
cnt++;
}
return cnt;
}
static boolean check(int X, int K) {
int[][] dp = new int[X + 1][K + 1];
dp[1][0] = 1;
for (int i = 2; i <= X; i++) {
for (int j = 1; j <= K; j++) {
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1] * numPrimes(i);
}
}
for (int j = 1; j <= K; j++) {
if (dp[X][j] > 0) {
return true;
}
}
return false;
}
}
|
Python3
import math
MAXN = 1005
def num_primes(n):
cnt = 0
for i in range(2, int(math.sqrt(n)) + 1):
while n % i == 0:
cnt += 1
n //= i
if n > 1:
cnt += 1
return cnt
def check(X, K):
dp = [[0] * (K + 1) for _ in range(X + 1)]
dp[1][0] = 1
for i in range(2, X + 1):
for j in range(1, K + 1):
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1] * num_primes(i)
for j in range(1, K + 1):
if dp[X][j] > 0:
return True
return False
X = 4
K = 2
if check(X, K):
print("Yes")
else:
print("No")
|
C#
using System;
public class DistinctPrimeFactors
{
const int MAXN = 1005;
public static int NumPrimes(int n)
{
int cnt = 0;
for (int i = 2; i * i <= n; i++)
{
while (n % i == 0)
{
cnt++;
n /= i;
}
}
if (n > 1)
{
cnt++;
}
return cnt;
}
public static bool Check(int X, int K)
{
int[][] dp = new int[X + 1][];
for (int i = 0; i <= X; i++)
{
dp[i] = new int[K + 1];
}
dp[1][0] = 1;
for (int i = 2; i <= X; i++)
{
for (int j = 1; j <= K; j++)
{
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1] * NumPrimes(i);
}
}
for (int j = 1; j <= K; j++)
{
if (dp[X][j] > 0)
{
return true;
}
}
return false;
}
public static void Main(string[] args)
{
int X = 4;
int K = 2;
if (Check(X, K))
{
Console.WriteLine("Yes");
}
else
{
Console.WriteLine("No");
}
}
}
|
Javascript
function numPrimes(n) {
let cnt = 0;
for (let i = 2; i * i <= n; i++) {
while (n % i === 0) {
cnt++;
n /= i;
}
}
if (n > 1) {
cnt++;
}
return cnt;
}
function check(X, K) {
const dp = new Array(X + 1).fill(0).map(() => new Array(K + 1).fill(0));
dp[1][0] = 1;
for (let i = 2; i <= X; i++) {
for (let j = 1; j <= K; j++) {
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1] * numPrimes(i);
}
}
for (let j = 1; j <= K; j++) {
if (dp[X][j] > 0) {
return true;
}
}
return false;
}
const X = 4;
const K = 2;
if (check(X, K)) {
console.log("Yes");
} else {
console.log("No");
}
|
Time Complexity: O(XKlog(X)), where X is the given number of factors and K is the given number of prime factors.
Auxiliary Space: O(X*K), where X is the given number of factors and K is the given number of prime factors.
Share your thoughts in the comments
Please Login to comment...