Check if each element of the given array is the product of exactly K prime numbers
Last Updated :
21 Jun, 2022
Given an array of numbers 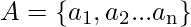 and the value of
and the value of 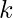 , check if each number
, check if each number 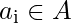 can be expressed as the product of exactly
can be expressed as the product of exactly 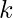 prime numbers. For every element of the array print ‘YES’ if the condition is satisfied, else print ‘NO’.
prime numbers. For every element of the array print ‘YES’ if the condition is satisfied, else print ‘NO’.
Note: Repeating prime numbers may also be considered. For example, if k = 2, then n = 4 (=2*2) is a valid input.
Let’s consider the number 36. 36 can be factorised as 2*2*3*3. Hence, it is the product of 4 prime numbers. If k value is 4, then the output should be YES. For other values of k, output should be NO.
More Examples:
Input: arr[] = {30, 8, 12}, K = 3
Output: YES, YES, YES
30 = 2*3*5
8 = 2*2*2
12 = 2*3*2
Input: arr[] = {30, 16, 32}, k = 5
Output: NO, NO, YES
Only 32 can be represented as product of
5 prime numbers.
In this article, we shall check if the given number(s) can be expressed as the product of exactly k prime numbers. The underlying concept that we shall we be using is simply a variation of the Sieve of Eratosthenes.
Recommended: How to construct the Sieve of Eratosthenes
Key Difference: In the Sieve, instead of storing binary values (0 if number not prime, 1 if the number is prime), we can store how many (repeating) prime factors make up that number instead. This modification is done during its construction.
The generalised procedure to create this modified sieve is as follows:
- Create an array full of 0’s to store the list of consecutive integers (2, 3, 4 … 10^6).
- Let the value of i be set to 2 initially. This is our first prime number.
- Loop through all the multiples of i (2*i, 3*i … till 10^6) by storing its value as j. Proceed with steps 3 and 4.
- Calculate the number of times j can be factorised using i and store the result into the variable count.
- When the number j cannot be further factorised using i, increment the value of Sieve[j] by the count value.
- Finally, find the next prime number greater than i in the list of integers. If there is no such number then terminate the process. Else, follow from step 2 again.
Explanation with example:
STEP 1:
The initialised empty sieve array looks as illustrated below. For simplicity’s sake let’s only concentrate on indices 2 through 12. The values stored initially is 0 for all indices.
Now, the first prime number that we will take is 2. This is the value of i.

STEP 2:
Initialise variable j to hold the value of every subsequent multiple of i starting from 2*i, which in this case is 4.

STEP 3:
The third step involves the computation of the prime factorisation of j. More specifically, we are just interested in counting the number of occurrences of i when you factorise j.
The computation procedure is simple. Just divide the value of j with i until you get a number that is not divisible by i. Here, 4 can be divided by 2 twice. 4/2 yields 2 and 2/2 yields 1, which is not divisible by 2 and the loop stops. Hence, we update the value of Sieve[4] with the value of the count variable, which is 2.

STEP 4:
We can proceed with the other elements in a similar fashion. Next, the value of j is 6. 6 can only be divided by 2 once. Hence the value of Sieve[6] is 1.


The final computed Sieve array should look something like this. Note that any index storing the value 0 represents a number that is not the product of 2 or more prime numbers. This includes all prime numbers, 0 and 1.
The second thing to note is that we need to only check

Below is the implementation of the above approach:
C++
#include <iostream>
#define MAX 1000000
using namespace std;
int Sieve[MAX] = { 0 };
void constructSieve()
{
for (int i = 2; i <= MAX; i++) {
if (Sieve[i] == 0) {
for (int j = 2 * i; j <= MAX; j += i) {
int temp = j;
while (temp > 1 && temp % i == 0) {
Sieve[j]++;
temp = temp / i;
}
}
}
}
}
void checkElements(int A[], int n, int k)
{
for (int i = 0; i < n; i++) {
if (Sieve[A[i]] == k) {
cout << "YES\n";
}
else {
cout << "NO\n";
}
}
}
int main()
{
constructSieve();
int k = 3;
int A[] = { 12, 36, 42, 72 };
int n = sizeof(A) / sizeof(int);
checkElements(A, n, k);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int MAX = 1000000;
static int[] Sieve = new int[MAX+1];
static void constructSieve()
{
for (int i = 2; i <= MAX; i++)
{
if (Sieve[i] == 0)
{
for (int j = 2 * i; j <= MAX; j += i)
{
int temp = j;
while (temp > 1 && temp % i == 0)
{
Sieve[j]++;
temp = temp / i;
}
}
}
}
}
static void checkElements(int A[], int n, int k)
{
for (int i = 0; i < n; i++)
{
if (Sieve[A[i]] == k)
{
System.out.println("YES");
}
else
{
System.out.println("No");
}
}
}
public static void main(String[] args)
{
constructSieve();
int k = 3;
int A[] = {12, 36, 42, 72};
int n = A.length;
checkElements(A, n, k);
}
}
|
Python3
MAX = 1000000
Sieve = [0]*(MAX + 1)
def constructSieve() :
for i in range(2, MAX + 1) :
if (Sieve[i] == 0) :
for j in range(2*i, MAX + 1, i) :
temp = j;
while (temp > 1 and temp % i == 0) :
Sieve[j] += 1;
temp = temp // i;
def checkElements(A, n, k) :
for i in range(n) :
if (Sieve[A[i]] == k) :
print("YES");
else :
print("NO");
if __name__ == "__main__" :
constructSieve();
k = 3;
A = [ 12, 36, 42, 72 ];
n = len(A);
checkElements(A, n, k);
|
C#
using System;
class GFG
{
static int MAX = 1000000;
static int[] Sieve = new int[MAX+1];
static void constructSieve()
{
for (int i = 2; i <= MAX; i++)
{
if (Sieve[i] == 0)
{
for (int j = 2 * i; j <= MAX; j += i)
{
int temp = j;
while (temp > 1 && temp % i == 0)
{
Sieve[j]++;
temp = temp / i;
}
}
}
}
}
static void checkElements(int []A, int n, int k)
{
for (int i = 0; i < n; i++)
{
if (Sieve[A[i]] == k)
{
Console.WriteLine("YES");
}
else
{
Console.WriteLine("No");
}
}
}
public static void Main()
{
constructSieve();
int k = 3;
int []A = {12, 36, 42, 72};
int n = A.Length;
checkElements(A, n, k);
}
}
|
Javascript
<script>
const MAX = 1000000;
let Sieve = new Array(MAX).fill(0);
function constructSieve()
{
for (let i = 2; i <= MAX; i++) {
if (Sieve[i] == 0) {
for (let j = 2 * i; j <= MAX; j += i)
{
let temp = j;
while (temp > 1 && temp % i == 0)
{
Sieve[j]++;
temp = parseInt(temp / i);
}
}
}
}
}
function checkElements(A, n, k)
{
for (let i = 0; i < n; i++) {
if (Sieve[A[i]] == k) {
document.write("YES<br>");
}
else {
document.write("NO<br>");
}
}
}
constructSieve();
let k = 3;
let A = [ 12, 36, 42, 72 ];
let n = A.length;
checkElements(A, n, k);
</script>
|
Time Complexity: O(n*log(logn)), where n is the length of the array A.
Space Complexity: O(MAX), where MAX is 106.
Share your thoughts in the comments
Please Login to comment...