Check if any large number is divisible by 17 or not
Last Updated :
31 Oct, 2023
Given a number, the task is to quickly check if the number is divisible by 17 or not.
Example:
Input : x = 34
Output : Yes
Input : x = 47
Output : No
A solution to the problem is to extract the last digit and subtract 5 times of the last digit from the remaining number and repeat this process until a two-digit number is obtained. If the obtained two-digit number is divisible by 17, then the given number is divisible by 17.
Approach:
- Extract the last digit of the number/truncated number every time
- Subtract 5*(last digit of the previous number) from the truncated number
- Repeat the above three steps as long as necessary.
Illustration:
3978-->397-5*8=357-->35-5*7=0.
So 3978 is divisible by 17.
Mathematical Proof :
Let 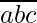 be any number such that
be any number such that 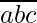 =100a+10b+c .
=100a+10b+c .
Now assume that 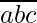 is divisible by 17. Then
is divisible by 17. Then
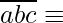 0 (mod 17)
0 (mod 17)
100a+10b+c 0 (mod 17)
0 (mod 17)
10(10a+b)+c 0 (mod 17)
0 (mod 17)
10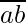 +c
+c 0 (mod 17)
0 (mod 17)
Now that we have separated the last digit from the number, we have to find a way to use it.
Make the coefficient of 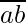 1.
1.
In other words, we have to find an integer such that n such that 10n 1 mod 17.
1 mod 17.
It can be observed that the smallest n which satisfies this property is -5 as -50 1 mod 17.
1 mod 17.
Now we can multiply the original equation 10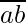 +c
+c 0 (mod 17)
0 (mod 17)
by -5 and simplify it:
-50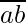 -5c
-5c 0 (mod 17)
0 (mod 17)
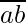 -5c
-5c 0 (mod 17)
0 (mod 17)
We have found out that if 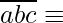 0 (mod 17) then,
0 (mod 17) then,
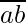 -5c
-5c 0 (mod 17).
0 (mod 17).
In other words, to check if a 3-digit number is divisible by 17,
we can just remove the last digit, multiply it by 5,
and then subtract it from the rest of the two digits.
Program :
C++
#include <bits/stdc++.h>
using namespace std;
bool isDivisible(long long int n)
{
while (n / 100)
{
int d = n % 10;
n /= 10;
n -= d * 5;
}
return (n % 17 == 0);
}
int main()
{
long long int n = 19877658;
if (isDivisible(n))
cout << "Yes" << endl;
else
cout << "No" << endl;
return 0;
}
|
Java
import java.io.*;
class GFG {
static boolean isDivisible(long n)
{
while (n / 100>0)
{
long d = n % 10;
n /= 10;
n -= d * 5;
}
return (n % 17 == 0);
}
public static void main (String[] args) {
long n = 19877658;
if (isDivisible(n))
System.out.println( "Yes");
else
System.out.println( "No");
}
}
|
Python 3
def isDivisible(n) :
while(n // 100) :
d = n % 10
n //= 10
n -= d * 5
return (n % 17 == 0)
if __name__ == "__main__" :
n = 19877658
if isDivisible(n) :
print("Yes")
else :
print("No")
|
C#
using System;
class GFG {
static bool isDivisible(long n)
{
while (n / 100>0)
{
long d = n % 10;
n /= 10;
n -= d * 5;
}
return (n % 17 == 0);
}
public static void Main () {
long n = 19877658;
if (isDivisible(n))
Console.Write( "Yes");
else
Console.Write( "No");
}
}
|
Javascript
function isDivisible(n) {
while (Math.floor(n / 100)) {
let d = n % 10;
n = Math.floor(n / 10);
n -= d * 5;
}
return n % 17 == 0;
}
let n = 19877658;
if (isDivisible(n))
console.log("Yes");
else
console.log("No");
|
PHP
<?php
function isDivisible($n)
{
while ($n / 100 != 0)
{
$d = (int)$n % 10;
$n /= 10;
$n -= $d * 5;
}
return ($n % 17 == 0);
}
$n = 19877658;
if (isDivisible($n))
print("Yes");
else
print("No");
?>
|
Time Complexity: O(log10n), time required to check if number is divisible by 17
Auxiliary Space: O(1), as no extra space is required
Note that the above program may not make a lot of sense as could simply do n % 23 to check for divisibility. The idea of this program is to validate the concept. Also, this might be an efficient approach if input number is large and given as string.
Approach 2: Dynamic Programming :
We can solve this problem using dynamic programming. Let’s define dp[i][j] as a boolean value that represents whether a number is divisible by 17 when we have processed the first i digits and the remainder obtained after dividing the number formed by the first i digits by 17 is j. We can fill this table in a bottom-up manner.
- The base case is dp[0][0] = true because an empty number is divisible by 17 with a remainder of 0.
- For each digit d at position i, we have two choices:
- We can ignore the digit and keep the remainder the same: dp[i][j] = dp[i-1][j].
We can include the digit and update the remainder: dp[i][j] = dp[i-1][(j – 5*d + 17) % 17]. - The final answer is given by dp[n][0] where n is the number of digits in the original number.
Here’s the implementation of the above approach:
C++
#include <iostream>
#include <cstring>
const int MAXN = 10;
bool isDivisibleBy17(int n) {
char str[MAXN];
sprintf(str, "%d", n);
int len = strlen(str);
bool dp[len+1][17];
memset(dp, false, sizeof(dp));
dp[0][0] = true;
for (int i = 1; i <= len; i++) {
int d = str[i-1] - '0';
for (int j = 0; j < 17; j++) {
dp[i][j] = dp[i-1][j];
if (j >= 5*d) {
dp[i][j] |= dp[i-1][(j - 5*d) % 17];
} else {
dp[i][j] |= dp[i-1][(j + 17 - 5*d) % 17];
}
}
}
return dp[len][0];
}
int main() {
const int n = 19877658;
std::cout << (isDivisibleBy17(n) ? "Yes" : "No") << std::endl;
return 0;
}
|
Java
import java.io.*;
public class Main {
public static boolean isDivisibleBy17(int n)
{
String strN = Integer.toString(n);
int lenN = strN.length();
boolean[][] dp = new boolean[lenN + 1][17];
dp[0][0] = true;
for (int i = 1; i <= lenN; i++) {
int d = Character.getNumericValue(
strN.charAt(i - 1));
for (int j = 0; j < 17; j++) {
dp[i][j]
= dp[i - 1][j];
if (j >= 5 * d) {
dp[i][j]
|= dp[i - 1][(j - 5 * d)
% 17];
}
else {
int index = (j + 17 - 5 * d) % 17;
if (index < 0) {
index += 17;
}
dp[i][j] |= dp[i - 1]
[index];
}
}
}
return dp[lenN][0];
}
public static void main(String[] args)
{
int n = 19877658;
if (isDivisibleBy17(n)) {
System.out.println("Yes");
}
else {
System.out.println("No");
}
}
}
|
Python3
def is_divisible_by_17(n):
str_n = str(n)
len_n = len(str_n)
dp = [[False for _ in range(17)] for _ in range(len_n + 1)]
dp[0][0] = True
for i in range(1, len_n + 1):
d = int(str_n[i-1])
for j in range(17):
dp[i][j] = dp[i-1][j]
if j >= 5*d:
dp[i][j] |= dp[i-1][(j - 5*d) % 17]
else:
dp[i][j] |= dp[i-1][(j + 17 - 5*d) % 17]
return dp[len_n][0]
n = 19877658
print("Yes" if is_divisible_by_17(n) else "No")
|
C#
using System;
class GFG {
public static bool IsDivisibleBy17(int n)
{
string strN = n.ToString();
int lenN = strN.Length;
bool[,] dp = new bool[lenN + 1, 17];
dp[0, 0] = true;
for (int i = 1; i <= lenN; i++) {
int d = int.Parse(strN[i - 1].ToString());
for (int j = 0; j < 17; j++) {
dp[i, j] = dp[i - 1, j];
if (j >= 5 * d) {
dp[i, j] |= dp[i - 1, (j - 5 * d) % 17];
} else {
int index = (j + 17 - 5 * d) % 17;
if (index < 0) {
index += 17;
}
dp[i, j] |= dp[i - 1, index];
}
}
}
return dp[lenN, 0];
}
public static void Main(string[] args)
{
int n = 19877658;
if (IsDivisibleBy17(n)) {
Console.WriteLine("Yes");
}
else {
Console.WriteLine("No");
}
}
}
|
Javascript
const MAXN = 10;
function isDivisibleBy17(n) {
const str = n.toString();
const len = str.length;
const dp = new Array(len + 1);
for (let i = 0; i <= len; i++) {
dp[i] = new Array(17).fill(false);
}
dp[0][0] = true;
for (let i = 1; i <= len; i++) {
const d = parseInt(str.charAt(i - 1));
for (let j = 0; j < 17; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= 5 * d) {
dp[i][j] |= dp[i - 1][(j - 5 * d) % 17];
} else {
dp[i][j] |= dp[i - 1][(j + 17 - 5 * d) % 17];
}
}
}
return dp[len][0];
}
const n = 19877658;
console.log(isDivisibleBy17(n) ? "Yes" : "No");
|
Time Complexity: O(N*17), where N is the number of digits in the input integer.
Auxiliary Space: O(N*17)
Share your thoughts in the comments
Please Login to comment...