Check if all the digits of the given number are same
Last Updated :
18 Sep, 2023
Given a positive integer N, the task is to check whether all the digits of the given integer N are the same or not. If found to be true, then print Yes. Otherwise, print No.
Examples:
Input: N = 222
Output: Yes
Input: N = 232
Output: No
Naive Approach: The simplest approach to solve the given problem is to iterate over all the digits of the given number N and if there exists any distinct digit then print Yes. Otherwise, print No.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
string checkSameDigits(int N)
{
int digit = N % 10;
while (N != 0)
{
int current_digit = N % 10;
N = N / 10;
if (current_digit != digit)
{
return "No";
}
}
return "Yes";
}
int main()
{
int N = 222;
cout << (checkSameDigits(N));
return 0;
}
|
Java
import java.io.*;
class GFG {
public static String checkSameDigits(int N)
{
int digit = N % 10;
while (N != 0) {
int current_digit = N % 10;
N = N / 10;
if (current_digit != digit) {
return "No";
}
}
return "Yes";
}
public static void main(String args[])
throws IOException
{
int N = 222;
System.out.println(
checkSameDigits(N));
}
}
|
Python3
def checkSameDigits(N) :
digit = N % 10;
while (N != 0) :
current_digit = N % 10;
N = N // 10;
if (current_digit != digit) :
return "No";
return "Yes";
if __name__ == "__main__" :
N = 222;
print(checkSameDigits(N));
|
C#
using System;
class GFG {
static string checkSameDigits(int N)
{
int digit = N % 10;
while (N != 0) {
int current_digit = N % 10;
N = N / 10;
if (current_digit != digit) {
return "No";
}
}
return "Yes";
}
public static void Main()
{
int N = 222;
Console.Write(checkSameDigits(N));
}
}
|
Javascript
<script>
function checkSameDigits(N)
{
var digit = N % 10;
while (N != 0)
{
var current_digit = N % 10;
N = parseInt(N / 10);
if (current_digit != digit)
{
return "No";
}
}
return "Yes";
}
var N = 222;
document.write(checkSameDigits(N));
</script>
|
Time Complexity: O(log10N)
Auxiliary Space: O(1)
Efficient Approach: The above approach can also be optimized by forming another number, say M of the same length of the given number N with the rightmost digit of N assuming N has all same digits and then comparing it with N. Now, M is of type (K*111….), where K is any digit from N.
Now to create the number M consisting of the only 1s, the sum of a Geometric Progression can be used as illustrated for the count of digits as 3:
Consider the first term(say a) as 1 and the common ratio(say r) as 10. Now for the value count of digits(say D) as 3 the sum of Geometric Progression is given by:
=> Sum = 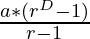
=> Sum = 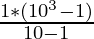
=> Sum = 
-> Sum = 111
From the above observations, generate the number M and check if K*M is the same as the N or not. If found to be true, then print Yes. Otherwise, print No.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
string checkSameDigits(int N)
{
int length = int(log10(N)) + 1;
int M = (int(pow(10, length)) - 1) / (10 - 1);
M *= N % 10;
if (M == N)
return "Yes";
return "No";
}
int main()
{
int N = 222;
cout << checkSameDigits(N);
}
|
Java
import java.io.*;
class GFG {
public static String checkSameDigits(int N)
{
int length = ((int)Math.log10(N)) + 1;
int M = ((int)Math.pow(10, length) - 1)
/ (10 - 1);
M *= N % 10;
if (M == N)
return "Yes";
return "No";
}
public static void main(String args[])
throws IOException
{
int N = 222;
System.out.println(
checkSameDigits(N));
}
}
|
Python3
import math
def checkSameDigits(N) :
length = int(math.log10(N)) + 1;
M = (int(math.pow(10, length)) - 1)// (10 - 1);
M *= N % 10;
if (M == N) :
return "Yes";
return "No";
if __name__ == "__main__" :
N = 222;
print(checkSameDigits(N));
|
C#
using System;
class GFG {
public static String checkSameDigits(int N)
{
int length = ((int)Math.Log10(N)) + 1;
int M = ((int)Math.Pow(10, length) - 1) / (10 - 1);
M *= N % 10;
if (M == N)
return "Yes";
return "No";
}
public static void Main()
{
int N = 222;
Console.WriteLine(checkSameDigits(N));
}
}
|
Javascript
<script>
function checkSameDigits(N)
{
var length = (Math.log10(N)) + 1;
var M = (Math.pow(10, length) - 1)
/ (10 - 1);
M *= N % 10;
if (M = N)
return "Yes";
return "No";
}
var N = 222;
document.write(checkSameDigits(N));
</script>
|
Time Complexity: O(logN)
Auxiliary Space: O(1)
Approach:
- Convert the given integer N to a string representation using the to_string function. This allows us to access individual digits as characters.
- Declare a variable digit and initialize it with the first character of the string str, which represents the first digit of the number.
- Iterate through the remaining characters of the string str, starting from the second character (index 1). Compare each character with the reference digit stored in digit.
- If any character is found to be different from the reference digit, return “No” indicating that not all digits are the same.
- If the loop completes without finding any different digit, return “Yes” indicating that all digits are the same.
Below is the implementation of the above approach:
C++
#include <iostream>
#include <string>
using namespace std;
string checkSameDigits(int N)
{
string str = to_string(N);
char digit = str[0];
for (int i = 1; i < str.length(); i++)
{
if (str[i] != digit)
{
return "No";
}
}
return "Yes";
}
int main()
{
int N = 222;
cout << checkSameDigits(N);
return 0;
}
|
Java
import java.util.*;
public class GFG {
public static String checkSameDigits(int N)
{
String str = Integer.toString(N);
char digit = str.charAt(0);
for (int i = 1; i < str.length(); i++) {
if (str.charAt(i) != digit) {
return "No";
}
}
return "Yes";
}
public static void main(String[] args)
{
int N = 222;
System.out.println(checkSameDigits(N));
}
}
|
Python3
def check_same_digits(N):
str_N = str(N)
digit = str_N[0]
for i in range(1, len(str_N)):
if str_N[i] != digit:
return "No"
return "Yes"
N = 222
print(check_same_digits(N))
|
C#
using System;
class GFG {
static string CheckSameDigits(int N)
{
string str_N = N.ToString();
char digit
= str_N[0];
for (int i = 1; i < str_N.Length; i++) {
if (str_N[i]
!= digit)
{
return "No";
}
}
return "Yes";
}
static void Main()
{
int N = 222;
Console.WriteLine(CheckSameDigits(N));
}
}
|
Javascript
function checkSameDigits(N) {
let str = N.toString();
let digit = str[0];
for (let i = 1; i < str.length; i++) {
if (str[i] !== digit) {
return "No";
}
}
return "Yes";
}
const N = 222;
console.log(checkSameDigits(N));
|
Time Complexity: O(d), where d is the number of digits in the given number N.
Auxiliary Space: O(d), where d is the number of digits in the given number N, The subsequent loop iterates through the characters of the string str, which also takes O(d) time.
Share your thoughts in the comments
Please Login to comment...