Check if a given directed graph is strongly connected | Set 2 (Kosaraju using BFS)
Last Updated :
12 Sep, 2023
Given a directed graph, find out whether the graph is strongly connected or not. A directed graph is strongly connected if there is a path between any two pairs of vertices. There are different methods to check the connectivity of directed graph but one of the optimized method is Kosaraju’s DFS based simple algorithm.
Kosaraju’s BFS based simple algorithm also work on the same principle as DFS based algorithm does.
Following is Kosaraju’s BFS based simple algorithm
that does two BFS traversals of graph:
1) Initialize all vertices as not visited.
2) Do a BFS traversal of graph starting from
any arbitrary vertex v. If BFS traversal
doesn’t visit all vertices, then return false.
3) Reverse all edges (or find transpose or reverse
of graph)
4) Mark all vertices as not visited in reversed graph.
5) Again do a BFS traversal of reversed graph starting
from same vertex v (Same as step 2). If BFS traversal
doesn’t visit all vertices, then return false.
Otherwise, return true.
The idea is again simple if every node can be reached from a vertex v, and every node can reach same vertex v, then the graph is strongly connected. In step 2, we check if all vertices are reachable from v. In step 5, we check if all vertices can reach v (In reversed graph, if all vertices are reachable from v, then all vertices can reach v in original graph).
Explanation with some examples:
Example 1 :
Given a directed to check if it is strongly connected or not.
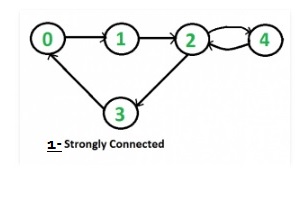
- step 1: Starting with vertex 2 BFS obtained is 2 3 4 0 1
- step 2: After reversing the given graph we got listed graph.
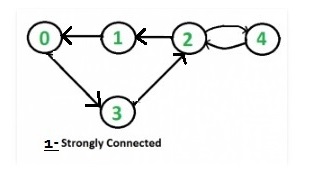
- step 3: Again after starting with vertex 2 the BFS is 2 1 4 0 3
- step 4: No vertex in both case (step 1 & step 3) remains unvisited.
- step 5: So, given graph is strongly connected.
Example 2 :
Given a directed to check if it is strongly connected or not.
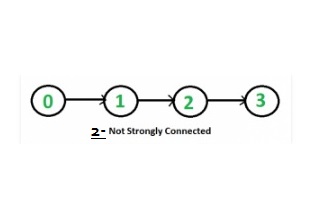
- step 1: Starting with vertex 2 BFS obtained is 2 3 4
- step 2: After reversing the given graph we got listed graph.
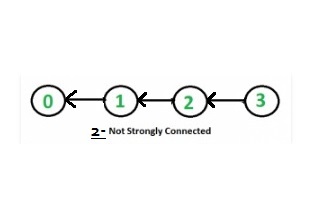
- step 3: Again after starting with vertex 2 the BFS is 2 1 0
- step 4: vertex 0, 1 in original graph and 3, 4 in reverse graph remains unvisited.
- step 5: So, given graph is not strongly connected.
Following is the implementation of above algorithm.
C++
#include <bits/stdc++.h>
using namespace std;
class Graph
{
int V;
list<int> *adj;
void BFSUtil(int v, bool visited[]);
public:
Graph(int V) { this->V = V; adj = new list<int>[V];}
~Graph() { delete [] adj; }
void addEdge(int v, int w);
bool isSC();
Graph getTranspose();
};
void Graph::BFSUtil(int v, bool visited[])
{
list<int> queue;
visited[v] = true;
queue.push_back(v);
list<int>::iterator i;
while (!queue.empty())
{
v = queue.front();
queue.pop_front();
for (i = adj[v].begin(); i != adj[v].end(); ++i)
{
if (!visited[*i])
{
visited[*i] = true;
queue.push_back(*i);
}
}
}
}
Graph Graph::getTranspose()
{
Graph g(V);
for (int v = 0; v < V; v++)
{
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
g.adj[*i].push_back(v);
}
return g;
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
}
bool Graph::isSC()
{
bool visited[V];
for (int i = 0; i < V; i++)
visited[i] = false;
BFSUtil(0, visited);
for (int i = 0; i < V; i++)
if (visited[i] == false)
return false;
Graph gr = getTranspose();
for(int i = 0; i < V; i++)
visited[i] = false;
gr.BFSUtil(0, visited);
for (int i = 0; i < V; i++)
if (visited[i] == false)
return false;
return true;
}
int main()
{
Graph g1(5);
g1.addEdge(0, 1);
g1.addEdge(1, 2);
g1.addEdge(2, 3);
g1.addEdge(3, 0);
g1.addEdge(2, 4);
g1.addEdge(4, 2);
g1.isSC()? cout << "Yes\n" : cout << "No\n";
Graph g2(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
g2.isSC()? cout << "Yes\n" : cout << "No\n";
return 0;
}
|
Java
import java.util.*;
class Graph {
int V;
ArrayList<ArrayList<Integer> > adj;
Graph(int V)
{
this.V = V;
adj = new ArrayList<>();
for (int i = 0; i < V; i++) {
adj.add(new ArrayList<>());
}
}
void addEdge(int v, int w)
{
adj.get(v).add(w);
}
void BFSUtil(int v, boolean visited[])
{
Queue<Integer> queue = new ArrayDeque<>();
visited[v] = true;
queue.add(v);
while (!queue.isEmpty())
{
v = queue.peek();
queue.remove();
for (Integer i : adj.get(v)) {
if (!visited[i]) {
visited[i] = true;
queue.add(i);
}
}
}
}
boolean isSC()
{
boolean[] visited = new boolean[V];
for (int i = 0; i < V; i++)
visited[i] = false;
BFSUtil(0, visited);
for (int i = 0; i < V; i++)
if (visited[i] == false)
return false;
Graph gr = getTranspose();
for (int i = 0; i < V; i++)
visited[i] = false;
gr.BFSUtil(0, visited);
for (int i = 0; i < V; i++)
if (visited[i] == false)
return false;
return true;
}
Graph getTranspose()
{
Graph g = new Graph(V);
for (int v = 0; v < V; v++) {
for (Integer i : adj.get(v))
g.adj.get(i).add(v);
}
return g;
}
}
public class GFG {
public static void main(String[] args)
{
Graph g1 = new Graph(5);
g1.addEdge(0, 1);
g1.addEdge(1, 2);
g1.addEdge(2, 3);
g1.addEdge(3, 0);
g1.addEdge(2, 4);
g1.addEdge(4, 2);
if (g1.isSC())
System.out.println("Yes");
else
System.out.println("No");
Graph g2 = new Graph(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
if (g2.isSC())
System.out.println("Yes");
else
System.out.println("No");
}
}
|
Python3
from collections import deque
def BFSUtil(adj, v, visited):
queue = deque()
visited[v] = True
queue.append(v)
while (len(queue) > 0):
v = queue.popleft()
for i in adj[v]:
if (visited[i] == False):
visited[i] = True
queue.append(i)
return visited
def getTranspose(adj, V):
g = [[] for i in range(V)]
for v in range(V):
for i in adj[v]:
g[i].append(v)
return g
def addEdge(adj, v, w):
adj[v].append(w)
return adj
def isSC(adj, V):
visited = [False]*V
visited = BFSUtil(adj, 0, visited)
for i in range(V):
if (visited[i] == False):
return False
adj = getTranspose(adj, V)
for i in range(V):
visited[i] = False
visited = BFSUtil(adj, 0, visited)
for i in range(V):
if (visited[i] == False):
return False
return True
if __name__ == '__main__':
g1 = [[] for i in range(5)]
g1 = addEdge(g1, 0, 1)
g1 = addEdge(g1, 1, 2)
g1 = addEdge(g1, 2, 3)
g1 = addEdge(g1, 3, 0)
g1 = addEdge(g1, 2, 4)
g1 = addEdge(g1, 4, 2)
print("Yes" if isSC(g1, 5) else "No")
g2 = [[] for i in range(4)]
g2 = addEdge(g2, 0, 1)
g2 = addEdge(g2, 1, 2)
g2 = addEdge(g2, 2, 3)
print("Yes" if isSC(g2, 4) else "No")
|
C#
using System;
using System.Collections.Generic;
using System.Linq;
class Graph
{
private int V;
private List<int>[] adj;
public Graph(int v)
{
V = v;
adj = new List<int>[v];
for (int i = 0; i < v; i++)
{
adj[i] = new List<int>();
}
}
public void addEdge(int v, int w)
{
adj[v].Add(w);
}
public bool isSC()
{
bool[] visited = new bool[V];
DFSUtil(0, visited);
for (int i = 0; i < V; i++)
{
if (visited[i] == false)
{
return false;
}
}
Graph gt = getTranspose();
for (int i = 0; i < V; i++)
{
visited[i] = false;
}
gt.DFSUtil(0, visited);
for (int i = 0; i < V; i++)
{
if (visited[i] == false)
{
return false;
}
}
return true;
}
private void DFSUtil(int v, bool[] visited)
{
visited[v] = true;
for (int i = 0; i < adj[v].Count; i++)
{
int n = adj[v][i];
if (!visited[n])
{
DFSUtil(n, visited);
}
}
}
private Graph getTranspose()
{
Graph g = new Graph(V);
for (int v = 0; v < V; v++)
{
for (int i = 0; i < adj[v].Count; i++)
{
g.adj[adj[v][i]].Add(v);
}
}
return g;
}
public static void Main(string[] args)
{
Graph g1 = new Graph(5);
g1.addEdge(0, 1);
g1.addEdge(1, 2);
g1.addEdge(2, 3);
g1.addEdge(3, 0);
g1.addEdge(2, 4);
g1.addEdge(4, 2);
if (g1.isSC())
Console.WriteLine("Yes");
else
Console.WriteLine("No");
Graph g2 = new Graph(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
if (g2.isSC())
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Javascript
<script>
class Graph
{
constructor(V){
this.V = V;
this.adj = new Array(V);
for(let i = 0; i < V; i++){
this.adj[i] = new Array();
}
}
BFSUtil(v, visited)
{
let queue = [];
visited[v] = true;
queue.push(v);
while (queue.length > 0)
{
v = queue[0];
queue.shift();
for (let i = 0; i < this.adj[v].length; i++)
{
let x = this.adj[v][i];
if (!visited[x])
{
visited[x] = true;
queue.push(x);
}
}
}
}
getTranspose()
{
let g = new Graph(this.V);
for (let v = 0; v < this.V; v++)
{
for (let i = 0; i < this.adj[v].length; i++){
let x = this.adj[v][i];
g.adj[x].push(v);
}
}
return g;
}
addEdge(v, w)
{
this.adj[v].push(w);
}
isSC()
{
let visited = new Array(this.V);
for (let i = 0; i < this.V; i++)
visited[i] = false;
this.BFSUtil(0, visited);
for (let i = 0; i < this.V; i++)
if (visited[i] == false)
return false;
let gr = this.getTranspose();
for(let i = 0; i < this.V; i++)
visited[i] = false;
gr.BFSUtil(0, visited);
for (let i = 0; i < this.V; i++)
if (visited[i] == false)
return false;
return true;
}
};
let g1 = new Graph(5);
g1.addEdge(0, 1);
g1.addEdge(1, 2);
g1.addEdge(2, 3);
g1.addEdge(3, 0);
g1.addEdge(2, 4);
g1.addEdge(4, 2);
if(g1.isSC()){
document.write("Yes");
}
else{
document.write("No");
}
let g2 = new Graph(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
if(g2.isSC()){
document.write("Yes");
}
else{
document.write("No");
}
</script>
|
Time Complexity: Time complexity of above implementation is same as Breadth First Search which is O(V+E) if the graph is represented using adjacency matrix representation.
Can we improve further?
The above approach requires two traversals of graph. We can find whether a graph is strongly connected or not in one traversal using Tarjan’s Algorithm to find Strongly Connected Components.
Share your thoughts in the comments
Please Login to comment...