Interest on Drawings is an interest charged on the amount withdrawn by the partners for personal use. Such interest is an income for the firm and an expense for the partners, and hence is credited to the Profit and Loss Appropriation Account of the firm and is deducted from the partner’s Capital/Current Account. Interest on drawings is to be charged when specifically provided in the Partnership Deed along with the rate of interest. Interest on drawings should be charged from the date of withdrawal of the amount till the date of the preparation of the Balance sheet. However, in case no date of withdrawal is mentioned, interest on drawings should be charged for the half-year (six months) on the whole amount based on the assumption that drawings are made evenly throughout the year.
Methods of Calculation of Interest of Drawings
Businesses use various methods for calculating interest on drawings according to the need and frequency of drawings in a particular year:
1. Simple Method
Under this method, interest on drawing is calculated separately for each amount withdrawn by the partner from the date of such drawings till the date of the balance sheet. The following formula is used to calculate interest on drawing:
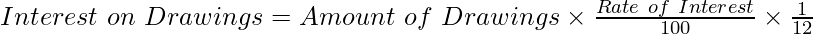
Illustration:
Amar being a partner of the Geeks partnership firm, withdrew ₹6,000 on 1st July 2020 for the year ending on 31st March, 2021. Calculate Interest on Drawings @ 9% p.a.
Solution:
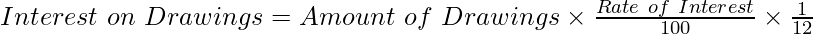
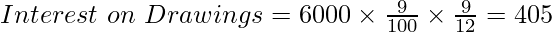
2. Product Method
Under this method, the first step is to evaluate the product by multiplying each amount of drawings by its duration. Then the total of all the products is used to compute the Interest on Drawings for one month. The following formula is used to calculate interest on drawing:
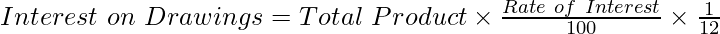
Illustration:
Amar being a partner of the GFG partnership firm, withdrew the following amounts during the year ended on 31st March, 2021:
| Date | Amount(₹) |
|---|
| May 1 | 6,000 |
| July 31 | 3,000 |
| September 30 | 4,500 |
| November 30 | 6,000 |
| January 1 | 4,000 |
| March 31 | 3,500 |
Calculate Interest on Drawings @9% p.a.
Solution:
Date of Withdrawal
| Period Due in Months
(Base on 31st March)
| Amount (₹)
| Product (₹)
(Amount X Period Due in Months)
|
|---|
| May 1 | 11
| 6,000
| 66,000
|
| July 31 | 8
| 3,000
| 24,000
|
| September 30 | 6
| 4,500
| 27,000
|
| November 30 | 4
| 6,000
| 24,000
|
| January 1 | 3
| 4,000
| 12,000
|
| March 31 | 0
| 3,500
| 0
|
| | | 27,000
| 1,53,000
|
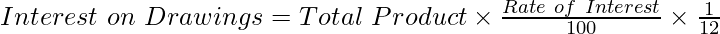
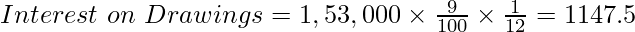
3. Interest on Monthly Drawings
Case A: When Drawings are made at the beginning of every month.
- When an unequal amount is withdrawn at the beginning of every month: Under such a situation, a product is calculated by multiplying the amount by the number of remaining months in that year,( for say, if the amount is withdrawn on July 1, then the number of remaining months in that year will be 9 months). The total of all products is then used to calculate the interest for one month based on the product method.
- When an equal amount is withdrawn at the beginning of every month: Under such a situation, the Average period shall be calculated using the formula:
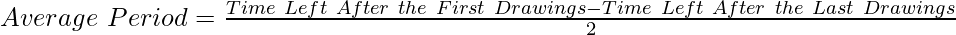
If the first amount is withdrawn on 1st April, the time left after the first drawing will be 12 months, and the time left after the last drawing, i.e., the last withdrawal is on 1st March, then the time left will be 1 month. Therefore,
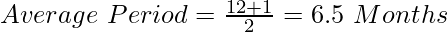
Note:
- The interest calculated for 6.5 months = The interest calculated on monthly basis.
- The average period is used only when an equal amount is withdrawn and at fixed intervals.
Case B : When Drawings are made at the end of every month:
- When an unequal amount is withdrawn at the end of every month: Under such a situation, the product is calculated by multiplying the amount by the number of remaining months in that year,( for example, if the amount is withdrawn on July 31, then the number of remaining months in that year will be 8 months). The total of all products is then used to calculate the interest for one month based on product method.
- When an equal amount is withdrawn at the end of every month: Under such a situation, the Average period shall be calculated using the formula:
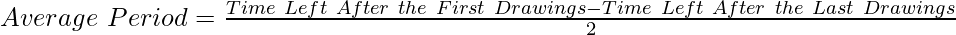
If the first amount is withdrawn on 30 April, the time left after the first drawing will be 11 months, and the time left after the last drawing, i.e., the last withdrawal is on March 30, then the time left will be 0 months. Therefore,
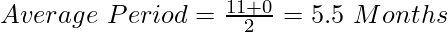
Note:
- The interest calculated for 5.5 months = The interest calculated on monthly basis.
- The average period is used only when an equal amount is withdrawn and at fixed intervals.
Case C: When Drawings are made in the middle of every month or at any time during a month.
Under such a situation, the Average period shall be calculated using the formula:
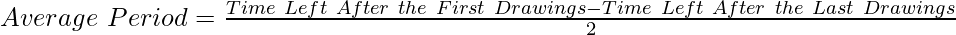
If the first amount is withdrawn on 15 April, the time left after the first drawing will be 11.5 months, and the time left after the last drawing, i.e., the last withdrawal is on March 15, then the time left will be 0.5 months. Therefore,
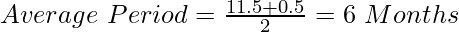
Interest on the whole amount will be calculated for 6 months.
Case D: When Drawings of equal amounts are made at the beginning of every quarter.
Under such a situation, the Average period shall be calculated using the formula:
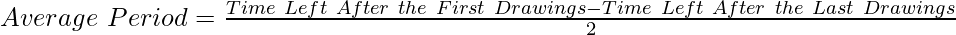
If the first amount is withdrawn on 1st April ( 1st day of the 1st quarter), the time left after the first drawing will be 12 months, and the time left after the last drawing, i.e., the last withdrawal is on 1st January, then the time left will be 3 months. Therefore,
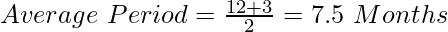
Case E: When Drawings of equal amounts are made at the end of every quarter.
Under such a situation, the Average period shall be calculated using the formula:
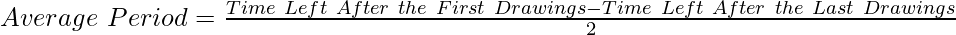
If the first amount is withdrawn on June 30 (The last day of the 1st quarter), the time left after the first drawing will be 9 months, and the time left after the last drawing, i.e., the last withdrawal is on March 30, then the time left will be 0 months. Therefore,
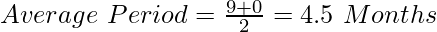
Case F: When Drawings of equal amounts are made during the middle of every quarter.
Under such a situation, the Average period shall be calculated using the formula:
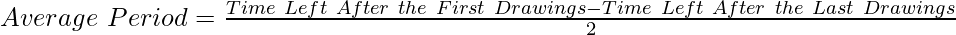
If the first amount is withdrawn on May 15 (The mid-day of the 1st quarter), the time left after the first drawing will be 10.5 months, and the time left after the last drawing, i.e., the last withdrawal is on February 15, then the time left will be 1.5 months. Therefore,
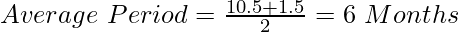
Interest on the whole amount will be calculated for 6 months.
Examples
Illustration:
Calculate Interest on Drawings @10% p.a. in each of the following cases:
Case (A): When ₹10,000 is withdrawn at the beginning of each month.
Case (B): When ₹10,000 is withdrawn at the end of each month.
Case (C): When ₹10,000 is withdrawn in the middle of each month.
Case (D): When ₹30,000 is withdrawn at the beginning of each quarter.
Case (E): When ₹30,000 is withdrawn at the end of each quarter.
Case (F): When ₹30,000 is withdrawn during the middle of each quarter.
Solution:
Case (A):
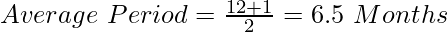
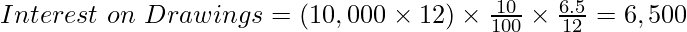
Case (B):
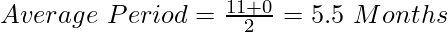
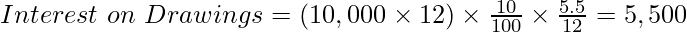
Case (C):
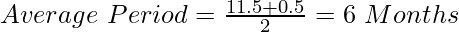
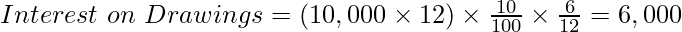
Case (D):
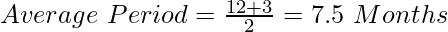
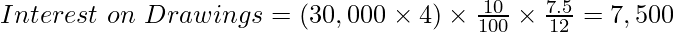
Case (E):
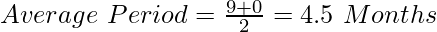
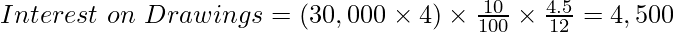
Case (F):
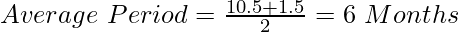
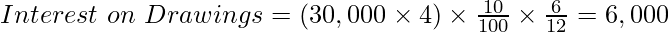
Share your thoughts in the comments
Please Login to comment...