Calculate MSE for random forest in R using package ‘randomForest’
Last Updated :
02 Aug, 2022
Random Forest is a supervised machine learning algorithm. It is an ensemble algorithm that uses an approach of bootstrap aggregation in the background to make predictions.
To learn more about random forest regression in R Programming Language refer to the below article –
Random Forest Approach for Regression in R Programming
As we know that random forest algorithm can be used for predicting both continuous values (regression) and discrete values (classification).In this article, we are going to read about how we can calculate the mean squared error for a random forest model built using the ‘randomForest’ library in R.
Mean squared error is an evaluation metric that is used to calculate the average squared difference between the actual value and the predicted value. MSE is a non-negative value that signifies how close a regression line is to the actual set of data points. To evaluate the performance of a regression model we use mean squared error (MSE). The closer the value of MSE to 0, the better the prediction will be. The mathematical equation for mean squared error is given as:
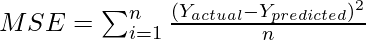
For the purpose of creating a model, the dataset we are using here is taken from the Dockship’s Power Plant Energy Prediction AI Challenge.
In this challenge, we need to predict the hourly power plant energy output. PE is the target column in our dataset. To know more about the dataset, please go through the challenge dashboard on the respective link shared above.
Calculate MSE for random forest in R using package ‘randomForest’
Step 1: In the first step, we will be importing the required libraries that we will be using in our program.
R
library("readr")
library("randomForest")
|
Here, we have imported two libraries named ‘readr’ and ‘randomForest’, the former helps us read and load data from a CSV file into the environment and the latter is used for creating the random forest model.
Step 2: We will start loading the dataset in our environment using the read_csv() function available in the “readr” library.
R
path <- "/power_plant_energy_prediction/TRAIN.csv"
content <- read_csv(path)
print(content)
|
Output:

Top 10 rows in the dataset
Step 3: To make a machine learning model, we need to train the model on a training set and then we will validate the performance of our model on a validation set. Hence, we will split the dataset into a training set named train_set and a validation set named val_set. The entire dataset contains 8000 rows, we will use the first 7000 rows in the train_set for learning and the rest 1000 rows for validation.
R
train_set <- content[1:7000,]
val_set <- tail(content, -7000)
|
Step 4: We will now use the randomForest() available in the ‘randomForest’ package to create a random forest model. We are using the train_set to train our model where PE is our target feature. The model is created using 100 trees for training purposes.
R
rf_model <- randomForest(PE~., data=train_set,
ntree=100,
importance=TRUE)
|
Step 5: Now, we will be using our trained random forest model to predict output values for our validation set which can be done using the predict() function by passing the trained model object i.e., rf_model, and the validation set i.e., val_set. The predicted values are stored inside the EnergyPred variable.
R
EnergyPred <- predict(rf_model, val_set)
|
Step 6: In this step, we will be evaluating the performance of our model by calculating the mean squared error between our actual and predicted values using the model. It can be done as:
R
print(mean((EnergyPred-val_set$PE)^2))
|
Output:
12:26536
The output that is generated is 12.26536 which is relatively closer to 0. Thus, we can say our model has decent performance on the validation set. We can even improve the performance of our random forest model by tuning the hyperparameters which help to reduce the overfitting and thus model performance can be improved.
Share your thoughts in the comments
Please Login to comment...