beta(), betaf() and betal() functions in C++ STL
Last Updated :
24 Oct, 2021
The beta(), betaf() and betal() are built-in functions in C++ STL that are used to compute the beta functionof two positive real values. The function takes two variables x and y as input and returns the beta function of x and y. Beta function (Also known as Euler integral of first kind) of x and y can be defined as:
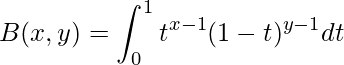
Syntax
double beta(double x, double y)
or
long double betal(long double x, long double y)
or
float betaf(float x, float y)
Parameters: The function accepts two mandatory parameters x and y which specifies the values of a floating-point or integral type. The parameters can be of double, double or float, float or long double, long double data-type.
Return Value: The function returns the value of beta function of x and y. The return type depends on the parameters passed. It is same as that of the parameter.
Note: The function runs in and above C++ 17(7.1).
Below program illustrates the beta(), betaf() and betal() functions:
CPP
#define __STDCPP_WANT_MATH_SPEC_FUNCS__ 1
#include <bits/stdc++.h>
using namespace std;
int main()
{
cout << beta(5, 4) << "\n";
cout << betaf(10.0, 4.0) << "\n";
cout << betal(10.0, 6.7) << "\n";
return 0;
}
|
Output:
0.00357143
0.00034965
1.65804e-005
Application of Beta function: It is used to compute Binomial Coefficients.The binomial coefficient in terms of beta function can be expressed as:

The above relation can be used to compute the binomial coefficient. An illustration has been shown below:
CPP
#define __STDCPP_WANT_MATH_SPEC_FUNCS__ 1
#include <bits/stdc++.h>
#include <cmath>
using namespace std;
double binomialCoefficient(int n, int k)
{
double ans = 1 / ((n + 1) * beta(n - k + 1, k + 1));
return ans;
}
int main()
{
cout << binomialCoefficient(5, 2) << "\n";
return 0;
}
|
Output:
10
Share your thoughts in the comments
Please Login to comment...