Axioms of Real Number System
Last Updated :
26 Apr, 2021
In this article, we shall look at some very basic ideas about the Real Analysis, i.e. the study of the structure of Real Number System. We shall discuss the three axioms that are considered to be satisfied by the set of Real Numbers, 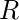
The three axioms are :
- Field Axioms
- Order Axioms
- Completeness Axiom
Field Axioms : The set 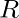 is represented as a field
is represented as a field 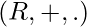 where
where 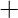 and
and  are the binary operations of addition and multiplication respectively. It consists of 4 axioms for addition and multiplication each and one distributive law.
are the binary operations of addition and multiplication respectively. It consists of 4 axioms for addition and multiplication each and one distributive law.
(i) Axioms for addition :
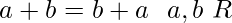
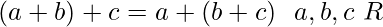
- R contains an element 0 such that
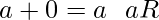
- For each
 there corresponds an element
there corresponds an element 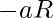 such that
such that 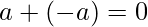
(ii) Axioms for multiplication :
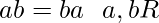
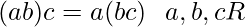
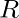 contains an element
contains an element 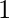 such that
such that 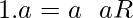 and
and 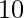
- If
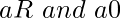 then there exists an element
then there exists an element 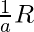 such that
such that 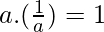
(iii) The distributive law :
Order Axioms : We define  (Greater Than) as the order relation, and it satisfies the following axioms –
(Greater Than) as the order relation, and it satisfies the following axioms –
- Law of Trichotomy – For
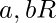 only one of the expressions can be true :
only one of the expressions can be true : 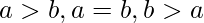
- Transitivity – For
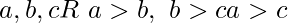
- Monotone Property for addition – For
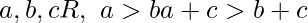
- Monotone Property for multiplication – For
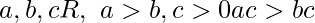
We call  linear order and
linear order and 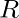 is called a linearly ordered field.
is called a linearly ordered field.
Before defining the Completeness Axiom, we shall look at the concept of Boundedness. Here, we shall define a few terms before stating the Completeness Axiom.
Aggregate : Any non empty subset, say 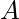 , of
, of 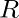 is known as an aggregate. For example, the set
is known as an aggregate. For example, the set 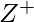 is an aggregate. Similarly, the set B = {1,2,4,8} is also an aggregate since
is an aggregate. Similarly, the set B = {1,2,4,8} is also an aggregate since 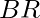 But, the set A = {x,y,z} and the empty set
But, the set A = {x,y,z} and the empty set  are not aggregates.
are not aggregates.
Upper bound : A subset 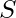 of
of 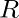 is said to be bounded above if
is said to be bounded above if 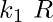 such that
such that 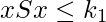 . This number
. This number  is called an upper bound of
is called an upper bound of 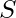 . For example, the set
. For example, the set 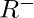 of negative real numbers is bounded above and
of negative real numbers is bounded above and 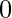 is an upper bound. Similarly, the set
is an upper bound. Similarly, the set  of negative integers is bounded above and
of negative integers is bounded above and 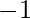 is the upper bound. But, the set
is the upper bound. But, the set 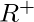 of positive real numbers is not bounded above.
of positive real numbers is not bounded above.
Lower Bound : A subset 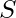 of
of 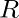 is said to be bounded below if
is said to be bounded below if 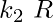 such that
such that 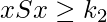 This number
This number 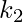 is called a lower bound of S. For example, the set
is called a lower bound of S. For example, the set 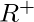 is bounded below and
is bounded below and 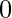 is a lower bound. Similarly, the set
is a lower bound. Similarly, the set 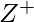 is bounded below and
is bounded below and 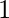 is the upper bound. But, the set
is the upper bound. But, the set 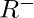 is not bounded below.
is not bounded below.
Least Upper Bound : Consider an upper bound 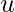 of an aggregate
of an aggregate 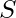 and any real number less than
and any real number less than 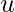 is not an upper bound of
is not an upper bound of 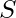 , then we say
, then we say 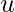 is the least upper bound(lub) or supremum(sup) of
is the least upper bound(lub) or supremum(sup) of 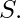
Greatest Lower bound : Consider a lower bound 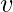 of an aggregate
of an aggregate 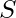 and any real number greater than
and any real number greater than 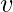 is not a lower bound of
is not a lower bound of 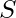 , then we say
, then we say 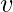 is the greatest lower bound(glb) or infimum(inf) of
is the greatest lower bound(glb) or infimum(inf) of 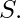
Example : Let ![Rendered by QuickLaTeX.com S = [0,1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e8ceb45cb7f6d58658dbe1e357682136_l3.png) . For S, we see that 1 is an upper bound and any number less than 1 is not an upper bound of S, hence, 1 is supremum of S. Also, 0 is a lower bound and any number greater than 0 is not a lower bound, so, 0 is infimum of S.
. For S, we see that 1 is an upper bound and any number less than 1 is not an upper bound of S, hence, 1 is supremum of S. Also, 0 is a lower bound and any number greater than 0 is not a lower bound, so, 0 is infimum of S.
Boundedness : An aggregate S is bounded if it is both bounded above and bounded below. That is, it must have both an upper bound and a lower bound. For example, any finite set is bounded, the empty set  is bounded. But, the sets
is bounded. But, the sets 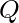 and
and 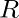 are not bounded.
are not bounded.
Note : An aggregate need not have a greatest and a least member to be bounded above or bounded below respectively.
Now being done with the required definition, we state the Completeness Axiom(also called the least upper bound axiom).
” Every non-empty set of Real numbers which is bounded above has a supremum.”
The set R satisfies the Field Axioms, Order Axioms, and the Completeness Axiom. Hence the set of real numbers 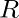 is called a complete ordered field.
is called a complete ordered field.
Also, the set of rational numbers, 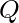 does not satisfy the completeness axiom. Hence,
does not satisfy the completeness axiom. Hence, 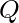 is not a complete field.
is not a complete field.
The completeness axiom is a really fundamental and important property of real number systems, as proofs various theorems of calculus, the concepts of maxima and minima, mean-value theorems etc. rely on the completeness property of real numbers.
Share your thoughts in the comments
Please Login to comment...