Arithmetic Progressions Class 10 Maths Notes Chapter 5

CBSE Class 10 Maths Notes Chapter 4 Arithmetic Progressions are an outstanding resource created by our team of knowledgeable Subject Experts at GfG. As ardent supporters of students’ education, we place a high priority on their learning and development, which is why we have written these in-depth notes to aid them in comprehending the challenging subject of arithmetic progressions.

Chapter 4 of the NCERT Class 10 Maths textbook finds the nth term of an arithmetic progression, summing the n terms of an arithmetic progression, calculating the arithmetic mean, and many other topics covered. These notes are intended to give students a thorough overview of the entire chapter, covering all the crucial topics, formulas, and ideas they will need to know to ace their examinations.

What is Arithmetic Progression?

An arithmetic progression is a numerical sequence formed by adding a fixed number to the prior term beginning with the first term so that the difference between the subsequent terms remains constant. It is abbreviated as A.P. Some examples of arithmetic progression are,

• 1, 4, 7, 10, 13, …
• 12, 7, 2, −3, −8, …
• −9, −7, −5, −3, …

First Term and Common Difference

If a sequence a₁,a₂,a₃,a₄,…..,a_n is an A.P. with a common difference d, then

a₂ − a₁ = d

a₃ − a₂ = d

a₄ − a₃ = d

.

.

.

a_n − a_n-1 = d and so on. 

and a₁ is the first term of the Sequence which is generally represented by a.

How to find the given Sequence is A.P. or Not?

To find whether any given sequence is A.P. or Not, we can use the following steps:

Step 1: Find a_n.

Step 2: Find a_n+1 by replacing n with n+1 in a_n.

Step 3: Evaluate a_n+1 − a_n.

Step 4: If the result found in step 3 is independent of n then the sequence is an A.P. otherwise not an A.P.

Example: Show that the sequence defined by a_n = 4n − 1 is an A.P.

Solution:

Here, a_n = 4n − 1

Replace n with n+1 in a_n.

     a_n+1 = 4(n + 1) − 1

⇒  a_n+1 = 4n + 4 − 1

⇒  a_n+1 = 4n + 3

Now, calculate the value of a_n+1 − a_n.

      a_n+1 − a_n = 4n + 3 − (4n − 1)

⇒  a_n+1 − a_n  = 4n + 3 − 4n + 1

⇒   a_n+1 − a_n = 4

The value of a_n+1 − a_n is a constant value and it is independent of n.

Hence, the sequence a_n = 4n −1 is an A.P.

Types of Arithmetic Progressions

We can classify the Arithmetic Progressions either based on the number of terms or signs of common difference. Let’s discuss these classifications in detail as follows:

Increasing and Decreasing APs

An A.P. is called Increasing if the common difference for the A.P. is positive i.e., terms of A.P. increases in value whereas A.P. is called decreasing if the common difference for A.P. is negative i.e.,  terms of A.P. decreases in value. “1, 2, 3, 4, . . ” is an example of increasing A.P. whereas “4, 1, -2, . . .” is an example of decreasing A.P.

Finite and Infinite APs

A.P. with a finite number of terms in it is called Finite A.P. whereas the Arithmetic Progressions with an endless number of terms are called Infinite A.P.  For example, 2, 4, 6, 8 is a finite AP with four terms. Similarly, 1, 4, 7, 10, and 13 are other examples of finite AP with five terms, and  “1, 2, 3, 4, …” is an infinite AP with a common difference of 1. Another example is “-3, -6, -9, -12, …,” which is an infinite AP with a common difference of -3.

n^th term of an A.P.

Let a represent the first term and d represents the common difference of an A.P. Then the n^th term or general term of an A.P. is,

a_n = a + (n − 1) d

OR

n^th term of an A.P. = First term + (Term’s Number − 1) × Common difference

Example: Find 10^th term of an A.P. −40, −15, 10, 35, ….

Solution:

Here, a = −40 and n = 10

Now, determine the common difference d.

    d = −15−(−40)

⇒ d = 25

Substitute −40 for a, 10 for n and 25 for d in a_n = a + (n − 1) d.

     a₁₀ = −40 + (10 − 1) 25

⇒  a₁₀ = −40 + (9)25

⇒  a₁₀ = 185

Therefore, 10^th term of an A.P. is 185.

n^th term of an A.P from the end

Let l represent the last term and d represent the common difference of an A.P. then the n^th term of an A.P. from the end is given as:

n^th term from the end = l − (n − 1) d

n^th term from the end = Last term + (Term number − 1) × Common difference

Example: Find 12^th term from the end of an A.P. 3, 5, 7, 9, …, 201.

Solution:

Here, l = 201 and n = 12

Now, determine the common difference d.

    d = 5 – 3

⇒ d = 2

Substitute 201 for l, 12 for n and 2 for d in n^th term from the end = l − (n − 1) d.

        12^th term from the end = 201 − (12 − 1) 2

 ⇒   12th term from the end = 201 −(11)2

⇒   12th term from the end = 179

Therefore, 12^th term from the end of an A.P. is 179.

Middle term of a finite A.P.

Let a represent the first term, d represents the common difference and n represents the number of terms of a finite A.P.

If n is odd, then ((n + 1) / 2)^th term is the middle term of a finite A.P.

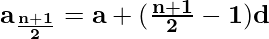
If n is odd, then (n / 2)^th and ((n / 2) + 1)^th terms are the middle term of a finite A.P.

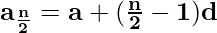 and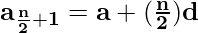 

Example: Find the middle term of an A.P. 213, 205, 197, …, 37.

Solution:

Here, a = 213 and a_n = 37

Now, determine the common difference d.

    d = 205 − 213

⇒ d = −8

Substitute 213 for a, 37 for a_n and −8 for d in a_n = a + (n − 1) d.

    37 = 213 + (n − 1) −8

⇒ 37 = 213 − 8n + 8

⇒ 8n = 213 + 8 – 37

⇒ 8n = 184

⇒   n = 23

Here, n is odd.

So, ((n + 1) / 2)^th term is the middle term of a finite A.P.

Substitute 213 for a, 23 for n and −8 for d in a_(n+1)/2 = a + (((n + 1) / 2) − 1) d.

   a_(23+1)/2 = 213 + (((23 + 1) / 2) − 1) −8

⇒       a₁₂ = 213+ (12 − 1) −8

⇒       a₁₂ = 213 − 88

⇒       a₁₂ = 125

Therefore, the middle term of an A.P. is 125.

Selection of terms in an A.P.

Number of terms	Terms	Common difference
3	a − d, a, a + d	d
4	a − 3d, a − d, a + d, a + 3d	2d
5	a − 2d, a − d, a, a + d, a + 2d	d
6	a − 5d, a − 3d, a − d , a + d, a + 3d, a + 5d	2d

It is noticed that if a number of terms is odd then the first term and common difference are a and d, if a number of terms are even then the first term and common difference are a and 2d.

Example: The sum of three numbers in A.P. is 12 and the sum of their cubes is 288. Find the numbers.

Solution:

Let a represents the first term and d represents the common difference.

So, the three numbers are a − d, a, and a + d.

It is given that the sum of three numbers is 12.

a − d + a + a + d = 12

⇒                   3a = 12

 ⇒                   a = 4

It is given that the sum of their cubes is 288.

(a − d)³ + a³ + (a + d)³ = 288

Substitute 4 for a in the above equation.

                                                      (4 − d)³ + 4³ + (4 + d)³ = 288

⇒ 4³ − d³ − 3(4)(d)(4 − d) + 64 + 4³ + d³ + 3(4)(d)(4 + d) = 288

 ⇒      64 − d³ − 48d + 12d² + 64 + 64 + d³ + 48d + 12d² = 288

 ⇒                                                                             24d² = 96

 ⇒                                                                                 d² = 4

  ⇒                                                                                 d = ±2

Case 1: When a = 4 and d = 2

The three numbers are 2, 4, and 6.

Case 2: When a = 4 and d = −2

The three numbers are 6, 4, and 2.

Sum of n terms of an A.P.

The sum S_n of n terms of an A.P. with the first term a and common difference d is,

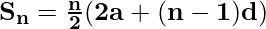
The sum S_n of n terms of an A.P. with last term l and common difference d is,

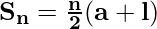
Note: The n^th term of a of the sequence is calculated by a_n = S_n − S_n-1

Sum of First n Natural Numbers

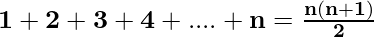
Example: Find the sum of all 2-digit natural numbers divisible by 4.

Solution:

The smallest 2-digit natural number is 10.

The largest 2-digit natural number is 99.

The smallest 2-digit natural number which is divisible by 4 is 12.

So, a = 12

The largest 2-digit natural number which is divisible by 4 is 96.

So, a_n = 96

The sequence of 2-digit natural number which are divisible by 4 are 12, 16, 20, 24, … , 96.

Now, determine the common difference d.

    d = 16 − 12

⇒ d = 4

Substitute 4 for d, 12 for a and 96 for a_n in a_n = a + (n − 1) d.

    96 = 12 + (n − 1) 4

⇒ 96 = 12 + 4n -4

⇒ 4n = 96 −12 + 4

⇒ 4n = 88

⇒   n = 22

Substitute 4 for d, 12 for a and 22 for n in S_n = n / 2 (2a + (n − 1) d )

    S₂₂ = 22/2 (2(12)+(22 − 1) 4)

⇒ S₂₂ = 11 (24 + (21) 4)

⇒ S₂₂ = 11 (24 + 84)

⇒ S₂₂ = 1188

Therefore, the sum of all 2-digit natural numbers divisible by 4 is 1188.

What is Arithmetic Mean?

The first two terms a and b will essentially have a difference, which will be equal to the next two terms b and c in the arithmetic progression if the three integers are in AP, which means if a, b, and c are in AP.

a − b = b − c

⇒ 2b = a + c

⇒   b = (a + b) / 2

Thus, the required arithmetic mean (A. M) of two number ‘a’ and ‘b’ is (a + b) / 2.

Some examples of arithmetic mean:

• The arithmetic mean between 12 and 32 in the arithmetic progression of 12, 22, and 32 is 22.
• The arithmetic mean between 7 and 11 in the arithmetic progression of 7, 9, and 11 is 9.

Example: In an A.M. the sum of three consecutive terms is −3 and their product is 8. Then find the terms.

Solution:

Let three consecutive terms are a, b and c.

It is given that the sum of three consecutive terms is −3.

So, a + b +c = −3.

It is given that the product of three consecutive terms is 8.

So, abc = 8.

According to the definition of A.M.,

2b = a + c

Substitute 2b for a + c in a + b +c = −3.

2b+ b = −3

⇒ 3b = −3

⇒   b = −1

Substitute −1 for b in 2b = a + c and then solve for a.

a + c = −2

⇒   a = −2 − c

Substitute −1 for b and −2 − c for a in abc = 8 and then solve for c.

                    (2 + c) c = 8

⇒              c² + 2c − 8=0

⇒     c² + 4c − 2c − 8 = 0

⇒ c(c + 4) − 2 (c + 4) = 0

⇒          (c + 4)(c − 2) = 0

⇒             c = − 4 or c = 2

Case 1: When c = − 4

Substitute −4 for c in a = −2 − c.

    a = −2 + 4

⇒ a = 2

Case 2: When c = 2

Substitute 2 for c in a = −2 − c.

    a = −2 − 2

⇒ a = −4

Therefore, the terms are −4, −1, 2 or 2, −1, −4.

FAQs on NCERT Notes for Class 10 Maths Chapter 4 Arithmetic Progressions

Q1. What is an Arithmetic Progression (AP)?

Answer:

An arithmetic progression is a numerical sequence formed by adding a fixed number to the prior term beginning with the first term, so that the difference between the subsequent terms remains constant. It is abbreviated as A.P.

Q2. What is the formula for the n^th term of an A.P.?

Answer:

a_n = a + ( n − 1) d where a be the first term and d be the common difference of an A.P.

Q3. How do you find the sum of the first n terms of an A.P.?

Answer:

S_n = n / 2 (2a + (n − 1) d ) where a be the first term and d be the common difference of an A.P.

Q4. How do you find the common difference of an A.P.?

Answer:

To find the common difference of an AP, you need to subtract any term from the term that comes after it. The result will be the common difference.

For example, let’s consider an AP with the first three terms as 2, 5, and 8. To find the common difference, we can subtract the second term from the first term or the third term from the second term.

Subtracting the second term from the first term: 5 – 2 = 3

Subtracting the third term from the second term: 8 – 5 = 3

Therefore, the common difference of this AP is 3.

Q5. What are some real-life applications of A.P.?

Answer:

Calculating interest rates, depreciation of assets, and even in the distribution of population over time