Algorithm for non recursive Predictive Parsing
Last Updated :
24 May, 2021
Prerequisite – Classification of Top Down Parsers
Predictive parsing is a special form of recursive descent parsing, where no backtracking is required, so this can predict which products to use to replace the input string.
Non-recursive predictive parsing or table-driven is also known as LL(1) parser. This parser follows the leftmost derivation (LMD).
LL(1):
here, first L is for Left to Right scanning of inputs,
the second L is for left most derivation procedure,
1 = Number of Look Ahead Symbols
The main problem during predictive parsing is that of determining the production to be applied for a non-terminal.
This non-recursive parser looks up which product to be applied in a parsing table. A LL(1) parser has the following components:
(1) buffer: an input buffer which contains the string to be passed
(2) stack: a pushdown stack which contains a sequence of grammar symbols
(3) A parsing table: a 2d array M[A, a]
where
A->non-terminal, a->terminal or $
(4) output stream:
end of the stack and an end of the input symbols are both denoted with $
Algorithm for non recursive Predictive Parsing:
The main Concept ->With the help of FIRST() and FOLLOW() sets, this parsing can be done using just a stack that avoids the recursive calls.
For each rule, A->x in grammar G:
- For each terminal ‘a’ contained in FIRST(A) add A->x to M[A, a] in the parsing table if x derives ‘a’ as the first symbol.
- If FIRST(A) contains null production for each terminal ‘b’ in FOLLOW(A), add this production (A->null) to M[A, b] in the parsing table.
The Procedure:
- In the beginning, the pushdown stack holds the start symbol of the grammar G.
- At each step a symbol X is popped from the stack:
if X is a terminal then it is matched with the lookahead and lookahead is advanced one step,
if X is a nonterminal symbol, then using lookahead and a parsing table (implementing the FIRST sets) a production is chosen and its right-hand side is pushed into the stack.
- This process repeats until the stack and the input string become null (empty).
Table-driven Parsing algorithm:
Input: a string w and a parsing table M for G.
tos top of the stack
Stack[tos++] <-$
Stack[tos++] <-Start Symbol
token <-next_token()
X <-Stack[tos]
repeat
if X is a terminal or $ then
if X = token then
pop X
token is next of token()
else error()
else /* X is a non-terminal */
if M[x, token] = X -> y1y2...yk then
pop x
push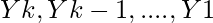 else error()
X Stack[tos]
until X = $
else error()
X Stack[tos]
until X = $
// Non-recursive parser model diagram:

So according to the given diagram the non-recursive parsing algorithm.
Input: A input string ‘w’ and a parsing table(‘M’) for grammar G.
Output: If w is in L(G), an LMD of w; otherwise an error indication.
Set input pointer to point to the first symbol of the string $;
repeat
let X be the symbol pointed by the stack pointer,
and a is the symbol pointed to by input pointer;
if X is a terminal or $ then
if X=a then
pop X from the stack and increment the input pointer;
else error()
end if
else /*if X is a non terminal */
if ![Rendered by QuickLaTeX.com M[X, a]= x->y1 y2 ...yk](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a1b179b8098043f960996344c8053ba9_l3.png) then
begin
pop X from the stack;
push
then
begin
pop X from the stack;
push 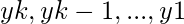 onto the stack, with Y1 on top;
output the production
onto the stack, with Y1 on top;
output the production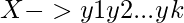 end
else error()
end if
end if
until X=$ /* stack is empty */
end
else error()
end if
end if
until X=$ /* stack is empty */
Example: Consider the subsequent LL(1) grammar:
S -> A
S -> ( S * A)
A -> id
Now let’s parse the given input:
( id * id )
The parsing table:
- row-> for each and every non-terminal symbol,
- column-> for each and every terminal (including the special terminal).
Each cell of this table will contain at most one rule of the given grammar:
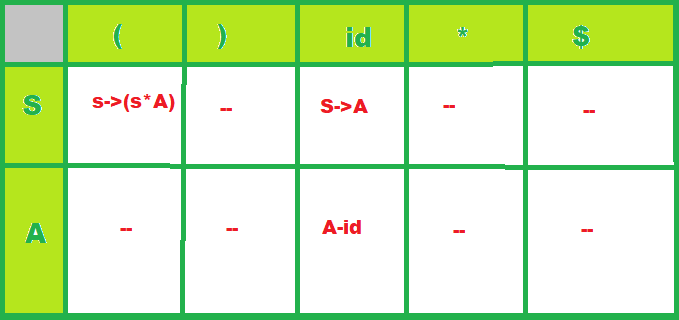
Now let’s see using the algorithm, how the parser uses this parsing table to process the given input.
Procedure:
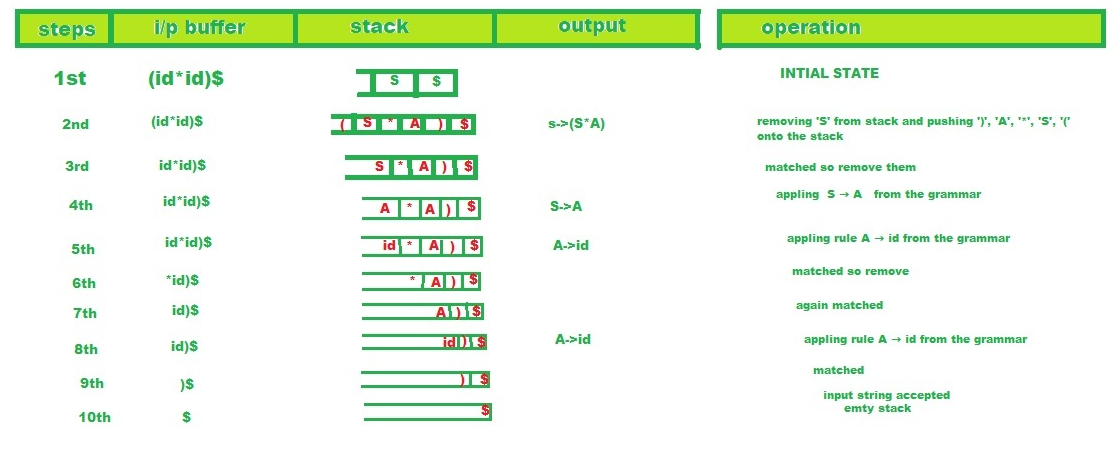
The parser thus ends because there remains only ‘$’ on both its stack and its input stream. In this case, the parser reports that it has accepted the input string and writes the following list of rules to the output stream:
S -> ( S * A),
S -> A,
A -> id,
A -> id
This is indeed a list of rules for an LMD of the input string, which is:
S -> ( S * A ) -> ( A * A ) -> ( id * A ) -> ( id * id )
Share your thoughts in the comments
Please Login to comment...