Construction of LL(1) Parsing Table

Prerequisite – Classification of top-down parsers, FIRST Set, FOLLOW Set

A top-down parser builds the parse tree from the top down, starting with the start non-terminal. There are two types of Top-Down Parsers: 

1. Top-Down Parser with Backtracking
2. Top-Down Parsers without Backtracking

Top-Down Parsers without backtracking can further be divided into two parts: 

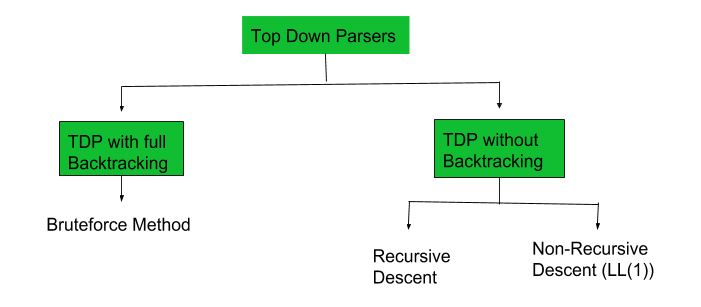
In this article, we are going to discuss Non-Recursive Descent which is also known as LL(1) Parser. 

LL(1) Parsing: Here the 1st L represents that the scanning of the Input will be done from the Left to Right manner and the second L shows that in this parsing technique, we are going to use the Left most Derivation Tree. And finally, the 1 represents the number of look-ahead, which means how many symbols are you going to see when you want to make a decision.

Essential conditions to check first are as follows: 

1. The grammar is free from left recursion.
2. The grammar should not be ambiguous.
3. The grammar has to be left factored in so that the grammar is deterministic grammar.

These conditions are necessary but not sufficient for proving a LL(1) parser.

Algorithm to construct LL(1) Parsing Table:

Step 1:  First check all the essential conditions mentioned above and go to step 2.

Step 2: Calculate First() and Follow() for all non-terminals.

1. First(): If there is a variable, and from that variable, if we try to drive all the strings then the beginning Terminal Symbol is called the First. 
2. Follow(): What is the Terminal Symbol which follows a variable in the process of derivation. 

Step 3: For each production A –> α. (A tends to alpha)

1. Find First(α) and for each terminal in First(α), make entry A –> α in the table.
2. If First(α) contains ε (epsilon) as terminal, then find the Follow(A) and for each terminal in Follow(A), make entry A –>  ε in the table.
3. If the First(α) contains ε and Follow(A) contains $ as terminal, then make entry A –>  ε in the table for the $.
   To construct the parsing table, we have two functions:  

In the table, rows will contain the Non-Terminals and the column will contain the Terminal Symbols. All the Null Productions of the Grammars will go under the Follow elements and the remaining productions will lie under the elements of the First set. 

Now, let’s understand with an example. 

Example 1: Consider the Grammar: 

E --> TE'
E' --> +TE' | ε                
T --> FT'
T' --> *FT' | ε
F --> id | (E)

*ε denotes epsilon

Step 1: The grammar satisfies all properties in step 1.

Step 2: Calculate first() and follow().

Find their First and Follow sets:  

	First	Follow
E –> TE’	{ id, ( }	{ $, ) }
E’ –> +TE’/ ε	{ +, ε }	{ $, ) }
T –> FT’	{ id, ( }	{ +, $, ) }
T’ –> *FT’/ ε	{ *, ε }	{ +, $, ) }
F –> id/(E)	{ id, ( }	{ *, +, $, ) }

Step 3: Make a parser table.

Now, the LL(1) Parsing Table is: 

	id	+	*	(	)	$
E	E –> TE’			E –> TE’
E’		E’ –> +TE’			E’ –> ε	E’ –> ε
T	T –> FT’			T –> FT’
T’		T’ –> ε	T’ –> *FT’		T’ –> ε	T’ –> ε
F	F –> id			F –> (E)

As you can see that all the null productions are put under the Follow set of that symbol and all the remaining productions lie under the First of that symbol. 

Note: Every grammar is not feasible for LL(1) Parsing table. It may be possible that one cell may contain more than one production. 

Let’s see an example. 

Example 2: Consider the Grammar 

S --> A | a
A --> a 

Step 1: The grammar does not satisfy all properties in step 1, as the grammar is ambiguous. Still, let’s try to make the parser table and see what happens

Step 2: Calculating first() and follow()

Find their First and Follow sets:

	First	Follow
S –> A/a	{ a }	{ $ }
A –>a	{ a }	{ $ }

Step 3: Make a parser table. 

Parsing Table: 

	a	$
S	S –> A, S –> a
A	A –> a

Here, we can see that there are two productions in the same cell. Hence, this grammar is not feasible for LL(1) Parser.

Trick –  Above grammar is ambiguous grammar. So the grammar does not satisfy the essential conditions. So we can say that this grammar is not feasible for LL(1) Parser even without making the parse table.

Example 3: Consider the Grammar 

S -> (L) | a
L -> SL'
L' -> )SL' | ε

Step1: The grammar satisfies all properties in step 1

Step 2: Calculating first() and follow()

	First	Follow
S	( , a	$, )
L	( , a	)
L’	), ε	)

Step 3: Making a parser table 

Parsing Table: 

	(	)	a	$
S	S -> (L)		S -> a
L	L -> SL’		L -> SL’
L’		L’->(SL’ L’->ε

Here, we can see that there are two productions in the same cell. Hence, this grammar is not feasible for LL(1) Parser. Although the grammar satisfies all the essential conditions in step 1, it is still not feasible for LL(1) Parser.  We saw in example 2 that we must have these essential conditions and in example 3 we saw that those conditions are insufficient to be a LL(1) parser. 

Advantages of Construction of LL(1) Parsing Table:

1.Deterministic Parsing: LL(1) parsing tables give a deterministic parsing process, truly intending that for a given information program and language structure, there is a novel not entirely set in stone by the ongoing non-terminal image and the lookahead token. This deterministic nature works on the parsing calculation and guarantees that the parsing system is unambiguous and unsurprising.

2.Efficiency: LL(1) parsing tables take into consideration productive parsing of programming dialects. When the parsing table is built, the parsing calculation can decide the following parsing activity by straightforwardly ordering the table, bringing about a steady time query. This productivity is particularly useful for huge scope programs and can altogether lessen the time expected for parsing.

3.Predictive Parsing: LL(1) parsing tables work with prescient parsing, where the parsing activity is resolved exclusively by the ongoing non-terminal image and the lookahead token without the requirement for backtracking or speculating. This prescient nature makes the LL(1) parsing calculation direct to execute and reason about. It likewise adds to better blunder dealing with and recuperation during parsing.

4.Error Discovery: The development of a LL(1) parsing table empowers the parser to proficiently distinguish mistakes. By dissecting the passages in the parsing table, the parser can recognize clashes, like various sections for a similar non-terminal and lookahead blend. These struggles demonstrate sentence structure ambiguities or mistakes in the syntax definition, considering early discovery and goal of issues.

5.Non-Left Recursion: LL(1) parsing tables require the disposal of left recursion in the language structure. While left recursion is a typical issue in syntaxes, the most common way of killing it brings about a more organized and unambiguous language structure. The development of a LL(1) parsing table energizes the utilization of non-left recursive creations, which prompts more clear and more effective parsing calculations.

6.Readability and Practicality: LL(1) parsing tables are by and large straightforward and keep up with. The parsing table addresses the whole parsing calculation in a plain configuration, with clear mappings between non-terminal images, lookahead tokens, and parsing activities. This plain portrayal works on the comprehensibility of the parsing calculation and improves on changes to the sentence structure, making it more viable over the long haul.

7.Language Plan: Building a LL(1) parsing table assumes a significant part in the plan and improvement of programming dialects. LL(1) language structures are frequently preferred because of their straightforwardness and consistency. By guaranteeing that a punctuation is LL(1) and building the related parsing table, language planners can shape the linguistic structure and characterize the normal way of behaving of the language all the more really.