Additive Congruence method for generating Pseudo Random Numbers
Last Updated :
11 Oct, 2022
Additive Congruential Method is a type of linear congruential generator for generating pseudorandom numbers in a specific range. This method can be defined as:
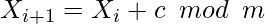
where,
X, the sequence of pseudo-random numbers
m ( > 0), the modulus
c [0, m), the increment
X0 [0, m), initial value of the sequence – termed as seed
m, c, X0 should be chosen appropriately to get a period almost equal to m.
Approach:
- Choose the seed value X0, modulus parameter m, and increment term c.
- Initialize the required amount of random numbers to generate (say, an integer variable noOfRandomNums).
- Define storage to keep the generated random numbers (here, vector is considered) of size noOfRandomNums.
- Initialize the 0th index of the vector with the seed value.
- For rest of indexes follow the Additive Congruential Method to generate the random numbers.
randomNums[i] = (randomNums[i – 1] + c) % m
Finally, return the generated random numbers.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void additiveCongruentialMethod(
int Xo, int m, int c,
vector<int>& randomNums,
int noOfRandomNums)
{
randomNums[0] = Xo;
for (int i = 1; i < noOfRandomNums; i++) {
randomNums[i]
= (randomNums[i - 1] + c)
% m;
}
}
int main()
{
int Xo = 3;
int m = 15;
int c = 2;
int noOfRandomNums = 20;
vector<int> randomNums(noOfRandomNums);
additiveCongruentialMethod(
Xo, m, c,
randomNums,
noOfRandomNums);
for (int i = 0; i < noOfRandomNums; i++) {
cout << randomNums[i] << " ";
}
return 0;
}
|
Java
class GFG{
static void additiveCongruentialMethod(
int Xo, int m, int c,
int []randomNums,
int noOfRandomNums)
{
randomNums[0] = Xo;
for(int i = 1; i < noOfRandomNums; i++)
{
randomNums[i] = (randomNums[i - 1] + c) % m;
}
}
public static void main(String[] args)
{
int Xo = 3;
int m = 15;
int c = 2;
int noOfRandomNums = 20;
int []randomNums = new int[noOfRandomNums];
additiveCongruentialMethod(Xo, m, c,
randomNums,
noOfRandomNums);
for(int i = 0; i < noOfRandomNums; i++)
{
System.out.print(randomNums[i] + " ");
}
}
}
|
Python3
def additiveCongruentialMethod(Xo, m, c,
randomNums,
noOfRandomNums):
randomNums[0] = Xo
for i in range(1, noOfRandomNums):
randomNums[i] = (randomNums[i - 1] + c) % m
if __name__ == '__main__':
Xo = 3
m = 15
c = 2
noOfRandomNums = 20
randomNums=[0] * (noOfRandomNums)
additiveCongruentialMethod(Xo, m, c,
randomNums,
noOfRandomNums)
for i in randomNums:
print(i, end = " ")
|
C#
using System;
class GFG{
static void additiveCongruentialMethod(
int Xo, int m, int c,
int []randomNums,
int noOfRandomNums)
{
randomNums[0] = Xo;
for(int i = 1; i < noOfRandomNums; i++)
{
randomNums[i] = (randomNums[i - 1] + c) % m;
}
}
public static void Main(String[] args)
{
int Xo = 3;
int m = 15;
int c = 2;
int noOfRandomNums = 20;
int []randomNums = new int[noOfRandomNums];
additiveCongruentialMethod(Xo, m, c,
randomNums,
noOfRandomNums);
for(int i = 0; i < noOfRandomNums; i++)
{
Console.Write(randomNums[i] + " ");
}
}
}
|
Javascript
<script>
function additiveCongruentialMethod(
Xo, m, c,
randomNums, noOfRandomNums)
{
randomNums[0] = Xo;
for(let i = 1; i < noOfRandomNums; i++)
{
randomNums[i] = (randomNums[i - 1] + c) % m;
}
}
let Xo = 3;
let m = 15;
let c = 2;
let noOfRandomNums = 20;
let randomNums = new Array(noOfRandomNums).fill(0);
additiveCongruentialMethod(Xo, m, c,
randomNums,
noOfRandomNums);
for(let i = 0; i < noOfRandomNums; i++)
{
document.write(randomNums[i] + " ");
}
</script>
|
Output: 3 5 7 9 11 13 0 2 4 6 8 10 12 14 1 3 5 7 9 11
Time complexity: O(N) where N is the count of random numbers to be generated.
Auxiliary space: O(N)
The literal meaning of pseudo is false. These random numbers are called pseudo because some known arithmetic procedure is utilized to generate. Even the generated sequence forms a pattern hence the generated number seems to be random but may not be truly random.
Share your thoughts in the comments
Please Login to comment...