Absolute Value

Absolute Value for a number x is denoted by |x|, pronounced as “module x”. It is ​​also referred to as numbers or magnitudes. Absolute values ​​are only numeric values ​​and do not include the sign of the numeric value.

Let’s learn about Absolute value in detail, including its symbol, properties, graph, and examples.

Absolute Value Meaning

Absolute value of a Number is the value of a number without any sign. We can define the absolute value of a function as the distance of a point from the origin and distance is never negative.

Absolute Value Symbol

The most common way to represent the absolute value of a number or expression is to enclose it in two vertical straight lines, called the absolute value symbol and represented by “| |“. 

eg. | +7 | = 7 .

Absolute values ​​always give non-negative values. So |+4|=|-4| =4. That is, it converts negative numbers to positive numbers.

Absolute Value Examples

Various examples of absolute value of numbers is,

• |-10| = 10
• |-4| = 4
• |12| = 12
• |0| = 0
• |5 – 3| = |2| = 2
• |6 – 9| = |-3| = 3
• |-3 × 4| = |-12| = 12

Absolute Values of a Number

If the number x is real, the absolute value satisfies the following condition: 

| x | = x   if x ≥ 0

| x | = – x if x ≤ 0 

Let’s look at the absolute value of x on the number line below. Here |x| is the distance of x from 0 (zero). So both +x and -x are at a distance of x from the origin.

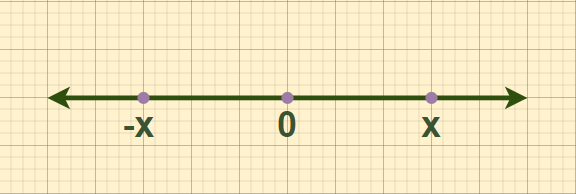
Since distance is not measured negatively, this counts as x.                                 

Absolute Value of 0

0 is neither positive nor negative, so the absolute value of 0 is  0. Since the distance of the number 0 is 0 to  0,  we can say that the absolute value of 0 is 0.

Absolute Value Function

Absolute Value of a function is given by,

f(x) = |x|

Its value is given by,

• |x| = +x for x > 0
• |x| = -x for x < 0

In the definition of an absolute value function, the value  |a| is,

|x| = +x or -x

We also know that,

√{x²} = +x or -x

Thus,

f(x) = |x| = √{x²}

Absolute Value Function Graph

The absolute value of a number is represented by |a|. This value or number represents the distance between a and 0 on a number line. Absolute value equations are equations that contain expressions for absolute values. The equation for absolute values ​​is: There are two forms of absolute value inequality. 

• |a| = +a for a≥ 0
• |a| = -a for a ≤ 0

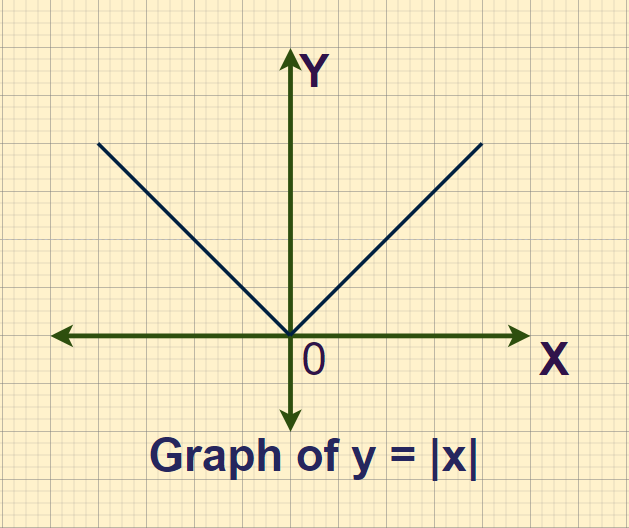
Absolute Value Function Graphs

Learn More:

• Function

Absolute Value Properties

If a, b and c are real numbers and their absolute values ​​satisfy the following properties:

Properties of Absolute Value
Property	Statement
Non-Negativity	Absolute of a number is always non-negative, | a | ≥ 0
Positive-Definiteness	|a| = 0 ↔ a = 0
Multiplicative Identity	|a × b| = |a| × |b|
Subadditivity	|a + b| ≤ |a| + |b|
Symmetry	|-a| = |a|
Identity of Indiscernible	|a – b| = 0 ↔ a = b
Triangle Inequality	|a – b| ≤ |a – c| + |c – b|
Preservation of Division	|a / b| = |a| / |b|
Equivalent to Subadditivity	|a ± b| ≥ | |a| – |b| |

Absolute Value of Real Number

For a real number the absolute value is the value of the number without any sign and it satisfies the condition,

• |x| = +x for a≥ 0
• |x| = -x for a ≤ 0

Where x is any real number.

Absolute Value of Complex Number

Complex numbers are made up of real and imaginary numbers. So, unlike integers, it is difficult to find absolute values. Assume that a + ib is a given complex number say,

z = a + ib

Absolute value of z is |z| = √[Re(z)² + Im(z)²]

|z| =√(a²+b²)

where a and b are  real numbers

Example, |3+ 4i|

= √(3²+4²)  

= √ (9 + 16)  

= √(25) = ±5

Learn More:

• Absolute Value of Complex Number

• Relation and Function
• Types of Functions
• Domain and Range

Examples of Absolute Value

Example 1: Solve 3 | x – 2 | = 15

Solution:

Given,

• 3| x – 2 | = 15

| x – 2 | = 5 

x – 2 = 5 or x – 2 = -5

x = 7 or x = -5 + 2 = -3

Example 2: Solve | 2x² – 1 | = | x² +  2 | 

Solution:

Given,

• | 2x² – 1 | = | x² + 2 |

Using Property, | x | = | y | ⇒  x = ± y

2x² – 1 = x² + 2 and 2x² – 1 = – ( x² +2 )

⇒ x² = 3 and  2x² -1 = -x² -2

⇒ x =  ±√ 3 and 3x² = -1 

⇒  x =  ±√ 3 and x = ±√( -1 / 3 ) = ± i / √ 3 =  ± √( 3 ) i/3

⇒  x =  ±√ 3 and x = ± (√3) i/3

Example 3: What is the value of 5 | 7x – 1 | if x = – 2 ?

Solution:

Given,

• Find the value of, 5| 7x – 1 | if, x = – 2

= 5 | 7(-2)  – 1 |

= 5 | -14 -1 |

= 5 | -15 |

= 5 ( 15 )

= 75

Value of 5 | 7x – 1 | = 75, when x = -2

Absolute Value Questions

Q1. Arrange in ascending order, |-1|, |2|, -|7|, |-9|, -|5|, |-18|, |-5|, |16|

Q2. Find the absolute value of a number -3/4

Q3. Find the absolute value of complex number 4 + 9i

Q4. Find the absolute value of complex number 3 – 2i

FAQs on Absolute Value

What is Absolute Value in Algebra?

The absolute value of a number is defined as a numeric value regardless of the sign of the number. It gives the distance from the  0 to the number on the number line. The absolute value of a number is always a non-negative number.

What is the Symbol of Absolute Value?

The symbol for absolute value is vertical bars: ∣⋅∣.

What is the Absolute Value of 0?

The absolute value of 0 is 0, i.e. |0| =0

What is the Absolute Value of -11?

The Absolute Value of -11 is 11.

What is the Absolute Value of – 4?

The absolute value of |-4| is 4.

What does |-15| mean?

|-15| means the absolute value of and its value is 15.

What is Absolute Value of 6?

The absolute value of 6 is represented as, |6| and its value is, 6.

What is the Use of Absolute Value?

The absolute value of the function or numbers is used to find the numeric value of function or number. These absolute values are found to find the value of price, lengths, volume and others.

Can Absolute Values be Negative?

The absolute value of any number or function is always positive. And it can not have any negative value, i.e. |± x| = x.

What is the Absolute Value of Complex Numbers?

For a complex number, z=a + bi, where a and b are real numbers and i is the imaginary unit (with the property that i²⁼ −1), the absolute value is defined as:

|z| =√(a²+b²)

where a and b are  real numbers