Wildcard Pattern Matching
Last Updated :
02 Nov, 2023
Given a text and a wildcard pattern, implement wildcard pattern matching algorithm that finds if wildcard pattern is matched with text. The matching should cover the entire text (not partial text). The wildcard pattern can include the characters ‘?’ and ‘*’
- ‘?’ – matches any single character
- ‘*’ – Matches any sequence of characters (including the empty sequence)
For example:
Text = "baaabab",
Pattern = “*****ba*****ab", output : true
Pattern = "baaa?ab", output : true
Pattern = "ba*a?", output : true
Pattern = "a*ab", output : false
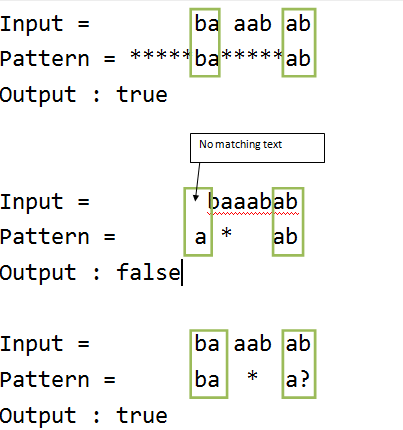
Each occurrence of ‘?’ character in wildcard pattern can be replaced with any other character and each occurrence of ‘*’ with a sequence of characters such that the wildcard pattern becomes identical to the input string after replacement.
Let’s consider any character in the pattern.
Case 1: The character is ‘*’ . Here two cases arises as follows:
- We can ignore ‘*’ character and move to next character in the Pattern.
- ‘*’ character matches with one or more characters in Text. Here we will move to next character in the string.
Case 2: The character is ‘?’
We can ignore current character in Text and move to next character in the Pattern and Text.
Case 3: The character is not a wildcard character
If current character in Text matches with current character in Pattern, we move to next character in the Pattern and Text. If they do not match, wildcard pattern and Text do not match.
We can use Dynamic Programming to solve this problem:
Let T[i][j] is true if first i characters in given string matches the first j characters of pattern.
Method 1:Using Backtracking(Brute Force)
Firstly we should be going thorugh the backtracking method:
The implementation of the code:
C++
#include <iostream>
using namespace std;
bool isMatch(string s, string p) {
int sIdx = 0, pIdx = 0, lastWildcardIdx = -1, sBacktrackIdx = -1, nextToWildcardIdx = -1;
while (sIdx < s.size()) {
if (pIdx < p.size() && (p[pIdx] == '?' || p[pIdx] == s[sIdx])) {
++sIdx;
++pIdx;
} else if (pIdx < p.size() && p[pIdx] == '*') {
lastWildcardIdx = pIdx;
nextToWildcardIdx = ++pIdx;
sBacktrackIdx = sIdx;
} else if (lastWildcardIdx == -1) {
return false;
} else {
pIdx = nextToWildcardIdx;
sIdx = ++sBacktrackIdx;
}
}
for(int i = pIdx; i < p.size(); i++){
if(p[i] != '*') return false;
}
return true;
}
int main() {
string str = "baaabab";
string pattern = "*****ba*****ab";
if (isMatch(str, pattern))
cout << "Yes" << endl;
else
cout << "No" << endl;
}
|
Java
class Main {
public static boolean isMatch(String s, String p) {
int sIdx = 0, pIdx = 0, lastWildcardIdx = -1, sBacktrackIdx = -1, nextToWildcardIdx = -1;
while (sIdx < s.length()) {
if (pIdx < p.length() && (p.charAt(pIdx) == '?' || p.charAt(pIdx) == s.charAt(sIdx))) {
++sIdx;
++pIdx;
} else if (pIdx < p.length() && p.charAt(pIdx) == '*') {
lastWildcardIdx = pIdx;
nextToWildcardIdx = ++pIdx;
sBacktrackIdx = sIdx;
} else if (lastWildcardIdx == -1) {
return false;
} else {
pIdx = nextToWildcardIdx;
sIdx = ++sBacktrackIdx;
}
}
for(int i = pIdx; i < p.length(); i++) {
if(p.charAt(i) != '*') {
return false;
}
}
return true;
}
public static void main(String[] args) {
String str = "baaabab";
String pattern = "*****ba*****ab";
if (isMatch(str, pattern)) {
System.out.println("Yes");
} else {
System.out.println("No");
}
}
}
|
Python
def isMatch(s, p):
m, n = len(s), len(p)
dp = [[False] * (n + 1) for _ in range(m + 1)]
dp[0][0] = True
for j in range(1, n + 1):
if p[j - 1] == '*':
dp[0][j] = dp[0][j - 1]
for i in range(1, m + 1):
for j in range(1, n + 1):
if p[j - 1] == '*':
dp[i][j] = dp[i - 1][j] or dp[i][j - 1]
elif p[j - 1] == '?' or p[j - 1] == s[i - 1]:
dp[i][j] = dp[i - 1][j - 1]
return dp[m][n]
str = "baaabab"
pattern = "*****ba*****ab"
if isMatch(str, pattern):
print("Yes")
else:
print("No")
|
C#
using System;
class Program {
static bool IsMatch(string s, string p) {
int sIdx = 0, pIdx = 0, lastWildcardIdx = -1, sBacktrackIdx = -1, nextToWildcardIdx = -1;
while (sIdx < s.Length) {
if (pIdx < p.Length && (p[pIdx] == '?' || p[pIdx] == s[sIdx])) {
++sIdx;
++pIdx;
} else if (pIdx < p.Length && p[pIdx] == '*') {
lastWildcardIdx = pIdx;
nextToWildcardIdx = ++pIdx;
sBacktrackIdx = sIdx;
} else if (lastWildcardIdx == -1) {
return false;
} else {
pIdx = nextToWildcardIdx;
sIdx = ++sBacktrackIdx;
}
}
for(int i = pIdx; i < p.Length; i++){
if(p[i] != '*') return false;
}
return true;
}
static void Main() {
string str = "baaabab";
string pattern = "*****ba*****ab";
if (IsMatch(str, pattern))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Javascript
function isMatch(s, p) {
let sIdx = 0, pIdx = 0, lastWildcardIdx = -1, sBacktrackIdx = -1, nextToWildcardIdx = -1;
while (sIdx < s.length) {
if (pIdx < p.length && (p[pIdx] === '?' || p[pIdx] === s[sIdx])) {
sIdx++;
pIdx++;
} else if (pIdx < p.length && p[pIdx] === '*') {
lastWildcardIdx = pIdx;
nextToWildcardIdx = ++pIdx;
sBacktrackIdx = sIdx;
} else if (lastWildcardIdx === -1) {
return false;
} else {
pIdx = nextToWildcardIdx;
sIdx = ++sBacktrackIdx;
}
}
for (let i = pIdx; i < p.length; i++) {
if (p[i] !== '*') return false;
}
return true;
}
const str = "baaabab";
const pattern = "*****ba*****ab";
if (isMatch(str, pattern))
console.log("Yes");
else
console.log("No");
|
Time complexity: O(m x n)
Auxiliary space: O(m x n)
DP Initialization:
// both text and pattern are null
T[0][0] = true;
// pattern is null
T[i][0] = false;
// text is null
T[0][j] = T[0][j - 1] if pattern[j – 1] is '*'
DP relation:
// If current characters match, result is same as
// result for lengths minus one. Characters match
// in two cases:
// a) If pattern character is '?' then it matches
// with any character of text.
// b) If current characters in both match
if ( pattern[j – 1] == ‘?’) ||
(pattern[j – 1] == text[i - 1])
T[i][j] = T[i-1][j-1]
// If we encounter ‘*’, two choices are possible-
// a) We ignore ‘*’ character and move to next
// character in the pattern, i.e., ‘*’
// indicates an empty sequence.
// b) '*' character matches with ith character in
// input
else if (pattern[j – 1] == ‘*’)
T[i][j] = T[i][j-1] || T[i-1][j]
else // if (pattern[j – 1] != text[i - 1])
T[i][j] = false
Implementation:
Below is the implementation of the above dynamic programming approach.
C++
#include <bits/stdc++.h>
using namespace std;
bool strmatch(char str[], char pattern[], int n, int m)
{
if (m == 0)
return (n == 0);
bool lookup[n + 1][m + 1];
memset(lookup, false, sizeof(lookup));
lookup[0][0] = true;
for (int j = 1; j <= m; j++)
if (pattern[j - 1] == '*')
lookup[0][j] = lookup[0][j - 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (pattern[j - 1] == '*')
lookup[i][j]
= lookup[i][j - 1] || lookup[i - 1][j];
else if (pattern[j - 1] == '?'
|| str[i - 1] == pattern[j - 1])
lookup[i][j] = lookup[i - 1][j - 1];
else
lookup[i][j] = false;
}
}
return lookup[n][m];
}
int main()
{
char str[] = "baaabab";
char pattern[] = "*****ba*****ab";
if (strmatch(str, pattern, strlen(str),
strlen(pattern)))
cout << "Yes" << endl;
else
cout << "No" << endl;
return 0;
}
|
Java
import java.util.Arrays;
public class GFG {
static boolean strmatch(String str, String pattern,
int n, int m)
{
if (m == 0)
return (n == 0);
boolean[][] lookup = new boolean[n + 1][m + 1];
for (int i = 0; i < n + 1; i++)
Arrays.fill(lookup[i], false);
lookup[0][0] = true;
for (int j = 1; j <= m; j++)
if (pattern.charAt(j - 1) == '*')
lookup[0][j] = lookup[0][j - 1];
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
if (pattern.charAt(j - 1) == '*')
lookup[i][j] = lookup[i][j - 1]
|| lookup[i - 1][j];
else if (pattern.charAt(j - 1) == '?'
|| str.charAt(i - 1)
== pattern.charAt(j - 1))
lookup[i][j] = lookup[i - 1][j - 1];
else
lookup[i][j] = false;
}
}
return lookup[n][m];
}
public static void main(String args[])
{
String str = "baaabab";
String pattern = "*****ba*****ab";
if (strmatch(str, pattern, str.length(),
pattern.length()))
System.out.println("Yes");
else
System.out.println("No");
}
}
|
Python3
def strrmatch(strr, pattern, n, m):
if (m == 0):
return (n == 0)
lookup = [[False for i in range(m + 1)] for j in range(n + 1)]
lookup[0][0] = True
for j in range(1, m + 1):
if (pattern[j - 1] == '*'):
lookup[0][j] = lookup[0][j - 1]
for i in range(1, n + 1):
for j in range(1, m + 1):
if (pattern[j - 1] == '*'):
lookup[i][j] = lookup[i][j - 1] or lookup[i - 1][j]
else if (pattern[j - 1] == '?' or strr[i - 1] == pattern[j - 1]):
lookup[i][j] = lookup[i - 1][j - 1]
else:
lookup[i][j] = False
return lookup[n][m]
strr = "baaabab"
pattern = "*****ba*****ab"
if (strrmatch(strr, pattern, len(strr), len(pattern))):
print("Yes")
else:
print("No")
|
C#
using System;
class GFG {
static Boolean strmatch(String str,
String pattern,
int n, int m)
{
if (m == 0)
return (n == 0);
Boolean[, ] lookup = new Boolean[n + 1, m + 1];
for (int i = 0; i < n + 1; i++)
for (int j = 0; j < m + 1; j++)
lookup[i, j] = false;
lookup[0, 0] = true;
for (int j = 1; j <= m; j++)
if (pattern[j - 1] == '*')
lookup[0, j] = lookup[0, j - 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (pattern[j - 1] == '*')
lookup[i, j] = lookup[i, j - 1]
|| lookup[i - 1, j];
else if (pattern[j - 1] == '?'
|| str[i - 1] == pattern[j - 1])
lookup[i, j] = lookup[i - 1, j - 1];
else
lookup[i, j] = false;
}
}
return lookup[n, m];
}
public static void Main(String[] args)
{
String str = "baaabab";
String pattern = "*****ba*****ab";
if (strmatch(str, pattern, str.Length,
pattern.Length))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Javascript
<script>
function strmatch(str, pattern, n, m)
{
if (m == 0)
return (n == 0);
let lookup = new Array(n + 1).fill(false).map(()=>new Array(m + 1).fill(false));
lookup[0][0] = true;
for (let j = 1; j <= m; j++)
if (pattern[j - 1] == '*')
lookup[0][j] = lookup[0][j - 1];
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= m; j++) {
if (pattern[j - 1] == '*')
lookup[i][j]
= lookup[i][j - 1] || lookup[i - 1][j];
else if (pattern[j - 1] == '?'
|| str[i - 1] == pattern[j - 1])
lookup[i][j] = lookup[i - 1][j - 1];
else
lookup[i][j] = false;
}
}
return lookup[n][m];
}
let str = "baaabab";
let pattern = "*****ba*****ab";
if (strmatch(str, pattern, str.length,pattern.length))
document.write("Yes","</br>")
else
document.write("No","</br>")
</script>
|
Time complexity: O(m x n)
Auxiliary space: O(m x n)
Approach: DP Memoization solution
C++
#include <bits/stdc++.h>
using namespace std;
vector<vector<int> > dp;
int finding(string& s, string& p, int n, int m)
{
if (n < 0 && m < 0)
return 1;
if (m < 0)
return 0;
if (n < 0) {
while (m >= 0) {
if (p[m] != '*')
return 0;
m--;
}
return 1;
}
if (dp[n][m] == -1) {
if (p[m] == '*') {
return dp[n][m] = finding(s, p, n - 1, m)
|| finding(s, p, n, m - 1);
}
else {
if (p[m] != s[n] && p[m] != '?')
return dp[n][m] = 0;
else
return dp[n][m]
= finding(s, p, n - 1, m - 1);
}
}
return dp[n][m];
}
bool isMatch(string s, string p)
{
dp.clear();
dp.resize(s.size() + 1, vector<int>(p.size() + 1, -1));
return dp[s.size()][p.size()]
= finding(s, p, s.size() - 1, p.size() - 1);
}
int main()
{
string str = "baaabab";
string pattern = "*****ba*****ab";
if (isMatch(str, pattern))
cout << "Yes" << endl;
else
cout << "No" << endl;
return 0;
}
|
Java
import java.util.*;
class WildcardMatching {
static int[][] dp;
static boolean finding(String s, String p, int n, int m) {
if (n < 0 && m < 0)
return true;
if (m < 0)
return false;
if (n < 0) {
while (m >= 0) {
if (p.charAt(m) != '*')
return false;
m--;
}
return true;
}
if (dp[n][m] == -1) {
if (p.charAt(m) == '*') {
dp[n][m] = (finding(s, p, n - 1, m) || finding(s, p, n, m - 1))?1:0;
return (dp[n][m] == 1);
} else {
if (p.charAt(m) != s.charAt(n) && p.charAt(m) != '?') {
dp[n][m] = 0;
return false;
} else {
dp[n][m] = (finding(s, p, n - 1, m - 1))?1:0;
return (dp[n][m] == 1);
}
}
}
return (dp[n][m] == 1);
}
static boolean isMatch(String s, String p) {
dp = new int[s.length() + 1][p.length() + 1];
for (int i = 0; i < s.length() + 1; i++) {
Arrays.fill(dp[i], -1);
}
return (finding(s, p, s.length() - 1, p.length() - 1) == true);
}
public static void main(String[] args) {
String str = "baaabab";
String pattern = "*****ba*****ab";
if (isMatch(str, pattern)) {
System.out.println("Yes");
} else {
System.out.println("No");
}
}
}
|
Python3
def finding(s, p, n, m):
if n < 0 and m < 0:
return 1
if m < 0:
return 0
if n < 0:
while m >= 0:
if p[m] != '*':
return 0
m -= 1
return 1
if dp[n][m] == -1:
if p[m] == '*':
dp[n][m] = finding(s, p, n - 1, m) or finding(s, p, n, m - 1)
return dp[n][m]
else:
if p[m] != s[n] and p[m] != '?':
dp[n][m] = 0
return dp[n][m]
else:
dp[n][m] = finding(s, p, n - 1, m - 1)
return dp[n][m]
return dp[n][m]
def isMatch(s, p):
global dp
dp = []
for i in range(len(s) + 1):
dp.append([-1] * (len(p) + 1))
dp[len(s)][len(p)] = finding(s, p, len(s) - 1, len(p) - 1)
return dp[len(s)][len(p)]
def main():
s = "baaabab"
p = "*****ba*****ab"
if isMatch(s, p):
print("Yes")
else:
print("No")
if __name__ == "__main__":
main()
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int finding(string s, string p, int n, int m, int[,]dp)
{
if (n < 0 && m < 0)
return 1;
if (m < 0)
return 0;
if (n < 0) {
while (m >= 0) {
if (p[m] != '*')
return 0;
m--;
}
return 1;
}
if (dp[n,m] == -1) {
if (p[m] == '*')
{
if((finding(s, p, n - 1, m, dp)==1) || (finding(s, p, n, m - 1, dp)==1))
{
dp[n,m]=1;
return dp[n,m];
}
}
else {
if (p[m] != s[n] && p[m] != '?')
return dp[n,m] = 0;
else
return dp[n,m]
= finding(s, p, n - 1, m - 1,dp);
}
}
return dp[n,m];
}
static int isMatch(string s, string p)
{
int [,]dp=new int[s.Length+1, p.Length+1];
for(int i=0; i<s.Length+1; i++)
{
for(int j=0; j<p.Length+1; j++)
dp[i,j]=-1;
}
return dp[s.Length,p.Length] = finding(s, p, s.Length - 1, p.Length - 1,dp);
}
public static void Main(String []args)
{
string str = "baaabab";
string pattern = "*****ba*****ab";
if (isMatch(str, pattern)==1)
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Javascript
<script>
let dp = [];
function finding(s, p, n, m)
{
if (n < 0 && m < 0)
return 1;
if (m < 0)
return 0;
if (n < 0)
{
while (m >= 0)
{
if (p[m] != '*')
return 0;
m--;
}
return 1;
}
if (dp[n][m] == -1)
{
if (p[m] == '*')
{
return dp[n][m] = finding(s, p, n - 1, m)
|| finding(s, p, n, m - 1);
}
else
{
if (p[m] != s[n] && p[m] != '?')
return dp[n][m] = 0;
else
return dp[n][m]
= finding(s, p, n - 1, m - 1);
}
}
return dp[n][m];
}
function isMatch(s, p)
{
dp = [];
dp = new Array(s.length+1).fill(1).map(()=>new Array(p.length+1).fill(-1));
return dp[s.length][p.length]
= finding(s, p, s.length - 1, p.length - 1);
}
let str = "baaabab";
let pattern = "*****ba*****ab";
if (isMatch(str, pattern))
console.log("Yes")
else
console.log("No")
</script>
|
Time complexity: O(m x n).
Auxiliary space: O(m x n).
Further Scope: We can improve space complexity by making use of the fact that we only uses the result from last row.
C++
#include <bits/stdc++.h>
using namespace std;
bool strmatch(char str[], char pattern[], int m, int n)
{
vector<bool> prev(m + 1, false), curr(m + 1, false);
prev[0] = true;
for (int i = 1; i <= n; i++) {
bool flag = true;
for (int ii = 1; ii < i; ii++) {
if (pattern[ii - 1] != '*') {
flag = false;
break;
}
}
curr[0] = flag;
for (int j = 1; j <= m; j++) {
if (pattern[i - 1] == '*')
curr[j] = curr[j - 1] || prev[j];
else if (pattern[i - 1] == '?'
|| str[j - 1] == pattern[i - 1])
curr[j] = prev[j - 1];
else
curr[j] = false;
}
prev = curr;
}
return prev[m];
}
int main()
{
char str[] = "baaabab";
char pattern[] = "*****ba*****ab";
if (strmatch(str, pattern, strlen(str),
strlen(pattern)))
cout << "Yes" << endl;
else
cout << "No" << endl;
return 0;
}
|
Java
import java.util.Arrays;
class Main {
public static boolean strmatch(String str, String pattern) {
boolean[] prev = new boolean[str.length() + 1];
boolean[] curr = new boolean[str.length() + 1];
prev[0] = true;
for (int i = 1; i <= pattern.length(); i++) {
boolean flag = true;
for (int ii = 1; ii < i; ii++) {
if (pattern.charAt(ii - 1) != '*') {
flag = false;
break;
}
}
curr[0] = flag;
for (int j = 1; j <= str.length(); j++) {
if (pattern.charAt(i - 1) == '*')
curr[j] = curr[j - 1] || prev[j];
else if (pattern.charAt(i - 1) == '?'
|| str.charAt(j - 1) == pattern.charAt(i - 1))
curr[j] = prev[j - 1];
else
curr[j] = false;
}
prev = Arrays.copyOf(curr, curr.length);
}
return prev[str.length()];
}
public static void main(String[] args) {
String str = "baaabab";
String pattern = "*****ba*****ab";
if (strmatch(str, pattern))
System.out.println("Yes");
else
System.out.println("No");
}
}
|
Python3
def strmatch(str, pattern, m, n):
prev, curr = [False]*(m+1), [False]*(m+1)
prev[0] = True
for i in range(1, n+1):
flag = True
for ii in range(1, i):
if pattern[ii-1] != '*':
flag = False
break
curr[0] = flag
for j in range(1, m+1):
if pattern[i-1] == '*':
curr[j] = curr[j-1] or prev[j]
elif pattern[i-1] == '?' or str[j-1] == pattern[i-1]:
curr[j] = prev[j-1]
else:
curr[j] = False
prev, curr = curr, prev
return prev[m]
if __name__ == '__main__':
str = "baaabab"
pattern = "*****ba*****ab"
if strmatch(str, pattern, len(str), len(pattern)):
print("Yes")
else:
print("No")
|
C#
using System;
class Program
{
public static bool StrMatch(string str, string pattern)
{
bool[] prev = new bool[str.Length + 1];
bool[] curr = new bool[str.Length + 1];
prev[0] = true;
for (int i = 1; i <= pattern.Length; i++) {
bool flag = true;
for (int ii = 1; ii < i; ii++) {
if (pattern[ii - 1] != '*') {
flag = false;
break;
}
}
curr[0] = flag;
for (int j = 1; j <= str.Length; j++)
{
if (pattern[i - 1] == '*')
curr[j] = curr[j - 1] || prev[j];
else if (pattern[i - 1] == '?'
|| str[j - 1] == pattern[i - 1])
curr[j] = prev[j - 1];
else
curr[j] = false;
}
prev = (bool[])curr.Clone();
}
return prev[str.Length];
}
public static void Main(string[] args) {
string str = "baaabab";
string pattern = "*****ba*****ab";
if (StrMatch(str, pattern))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Javascript
function strmatch(str, pattern, m, n) {
let prev = new Array(m + 1).fill(false);
let curr = new Array(m + 1).fill(false);
prev[0] = true;
for (let i = 1; i <= n; i++) {
let flag = true;
for (let ii = 1; ii < i; ii++) {
if (pattern[ii - 1] != '*') {
flag = false;
break;
}
}
curr[0] = flag;
for (let j = 1; j <= m; j++) {
if (pattern[i - 1] == '*')
curr[j] = curr[j - 1] || prev[j];
else if (pattern[i - 1] == '?'
|| str[j - 1] == pattern[i - 1])
curr[j] = prev[j - 1];
else
curr[j] = false;
}
prev = curr.slice();
}
return prev[m];
}
let str = "baaabab";
let pattern = "*****ba*****ab";
if (strmatch(str, pattern, str.length, pattern.length))
console.log("Yes");
else
console.log("No");
|
Time complexity: O(m x n).
Auxiliary space: O(m).
Approach: Greedy Method
We know in the greedy algorithm, we always find the temporary best solution and hope that it leads to a globally best or optimal solution.
At first, we initialize two pointers i and j to the beginning of the text and the pattern, respectively. We also initialize two variables startIndex and match to -1 and 0, respectively. startIndex will keep track of the position of the last ‘*’ character in the pattern, and match will keep track of the position in the text where the last proper match started.
We then loop through the text until we reach the end or find a character in the pattern that doesn’t match the corresponding character in the text. If the current characters match, we simply move to the next characters in both the pattern and the text. Ifnd if the pattern has a ‘?’ , we simply move to the next characters in both the pattern and the text. If the pattern has a ‘ ‘ character, then we mark the current position in the pattern and the text as a proper match by setting startIndex to the current position in the pattern and its match to the current position in the text. If there was no match and no ‘ ‘ character, then we understand we need to go through a different route henceforth, we backtrack to the last ‘*’ character position and try a different match by setting j to startIndex + 1, match to match + 1, and i to match.
Once we have looped over the text, we consume any remaining ‘*’ characters in the pattern, and if we have reached the end of both the pattern and the text, the pattern matches the text.
Implementation:
Below is the implementation of the above greedy approach.
C++
#include <iostream>
using namespace std;
bool isMatch(string text, string pattern)
{
int n = text.length();
int m = pattern.length();
int i = 0, j = 0, startIndex = -1, match = 0;
while (i < n)
{
if (j < m && (pattern[j] == '?' || pattern[j] == text[i]))
{
i++;
j++;
}
else if (j < m && pattern[j] == '*')
{
startIndex = j;
match = i;
j++;
}
else if (startIndex != -1)
{
j = startIndex + 1;
match++;
i = match;
}
else
{
return false;
}
}
while (j < m && pattern[j] == '*')
{
j++;
}
return j == m;
}
int main()
{
string str = "baaabab";
string pattern = "*****ba*****ab";
if (isMatch(str, pattern))
cout << "Yes" << endl;
else
cout << "No" << endl;
}
|
Java
import java.io.*;
class GFG {
public static boolean isMatch(String text, String pattern)
{
int n = text.length();
int m = pattern.length();
int i = 0, j = 0, startIndex = -1, match = 0;
while (i < n) {
if (j < m&& (pattern.charAt(j) == '?'|| pattern.charAt(j)== text.charAt(i))) {
i++;
j++;
}
else if (j < m && pattern.charAt(j) == '*') {
startIndex = j;
match = i;
j++;
}
else if (startIndex != -1) {
j = startIndex + 1;
match++;
i = match;
}
else {
return false;
}
}
while (j < m && pattern.charAt(j) == '*') {
j++;
}
return j == m;
}
public static void main(String[] args)
{
String str = "baaabab";
String pattern = "*****ba*****ab";
if (isMatch(str, pattern))
System.out.println("Yes");
else
System.out.println("No");
}
}
|
Python3
def isMatch(text, pattern):
n = len(text)
m = len(pattern)
i = 0
j = 0
startIndex = -1
match = 0
while i < n:
if j < m and (pattern[j] == '?' or pattern[j] == text[i]):
i += 1
j += 1
elif j < m and pattern[j] == '*':
startIndex = j
match = i
j += 1
elif startIndex != -1:
j = startIndex + 1
match += 1
i = match
else:
return False
while j < m and pattern[j] == '*':
j += 1
return j == m
str = "baaabab"
pattern = "*****ba*****ab"
if isMatch(str, pattern):
print("Yes")
else:
print("No")
|
C#
using System;
class Solution {
static bool IsMatch(string text, string pattern)
{
int n = text.Length;
int m = pattern.Length;
int i = 0, j = 0, startIndex = -1, match = 0;
while (i < n) {
if (j < m
&& (pattern[j] == '?'
|| pattern[j] == text[i])) {
i++;
j++;
}
else if (j < m && pattern[j] == '*') {
startIndex = j;
match = i;
j++;
}
else if (startIndex != -1) {
j = startIndex + 1;
match++;
i = match;
}
else {
return false;
}
}
while (j < m && pattern[j] == '*') {
j++;
}
return j == m;
}
static void Main()
{
string str = "baaabab";
string pattern = "*****ba*****ab";
if (IsMatch(str, pattern))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Javascript
function isMatch(text, pattern) {
let n = text.length;
let m = pattern.length;
let i = 0, j = 0, startIndex = -1, match = 0;
while (i < n) {
if (j < m && (pattern[j] === '?' || pattern[j] === text[i])) {
i++;
j++;
} else if (j < m && pattern[j] === '*') {
startIndex = j;
match = i;
j++;
} else if (startIndex !== -1) {
j = startIndex + 1;
match++;
i = match;
} else {
return false;
}
}
while (j < m && pattern[j] === '*') {
j++;
}
return j === m;
}
const str = "baaabab";
const pattern = "*****ba*****ab";
if (isMatch(str, pattern))
console.log("Yes");
else
console.log("No");
|
Time Complexity: O(n), where n is the length of the given text.
Auxiliary Space: O(1), because we only use constant amount of extra memory to store just the two pointers.
One more improvement is you can merge consecutive ‘*’ in the pattern to single ‘*’ as they mean the same thing. For example for pattern “*****ba*****ab”, if we merge consecutive stars, the resultant string will be “*ba*ab”. So, value of m is reduced from 14 to 6.
This article is contributed by Aditya Goel.
Share your thoughts in the comments
Please Login to comment...