QuickSort – Data Structure and Algorithm Tutorials
Last Updated :
09 Apr, 2024
QuickSort is a sorting algorithm based on the Divide and Conquer algorithm that picks an element as a pivot and partitions the given array around the picked pivot by placing the pivot in its correct position in the sorted array.
How does QuickSort work?
The key process in quickSort is a partition(). The target of partitions is to place the pivot (any element can be chosen to be a pivot) at its correct position in the sorted array and put all smaller elements to the left of the pivot, and all greater elements to the right of the pivot.
Partition is done recursively on each side of the pivot after the pivot is placed in its correct position and this finally sorts the array.
How Quicksort works
Choice of Pivot:
There are many different choices for picking pivots.
Partition Algorithm:
The logic is simple, we start from the leftmost element and keep track of the index of smaller (or equal) elements as i. While traversing, if we find a smaller element, we swap the current element with arr[i]. Otherwise, we ignore the current element.
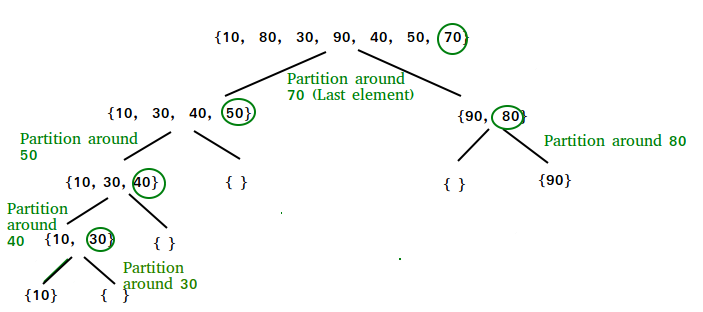
Let us understand the working of partition and the Quick Sort algorithm with the help of the following example:
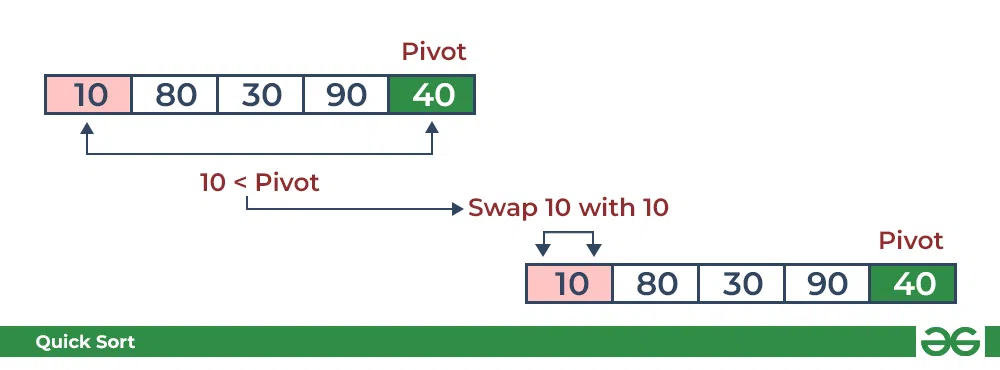
Consider: arr[] = {10, 80, 30, 90, 40}.
- Compare 10 with the pivot and as it is less than pivot arrange it accrodingly.
Partition in QuickSort: Compare pivot with 10
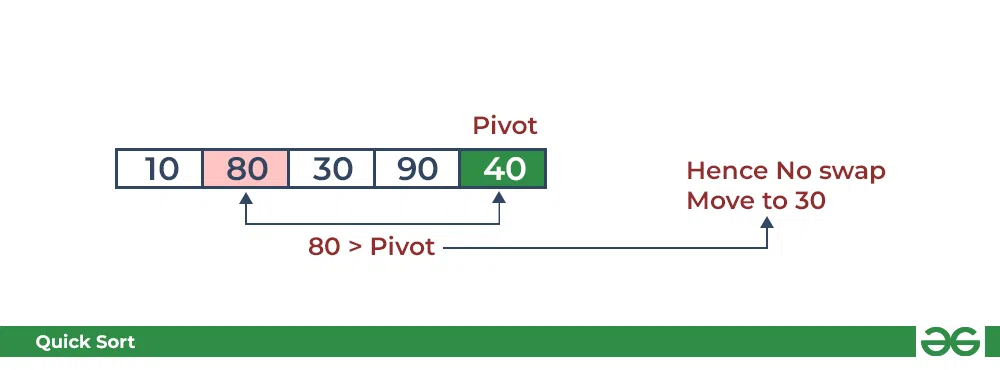
- Compare 80 with the pivot. It is greater than pivot.
Partition in QuickSort: Compare pivot with 80
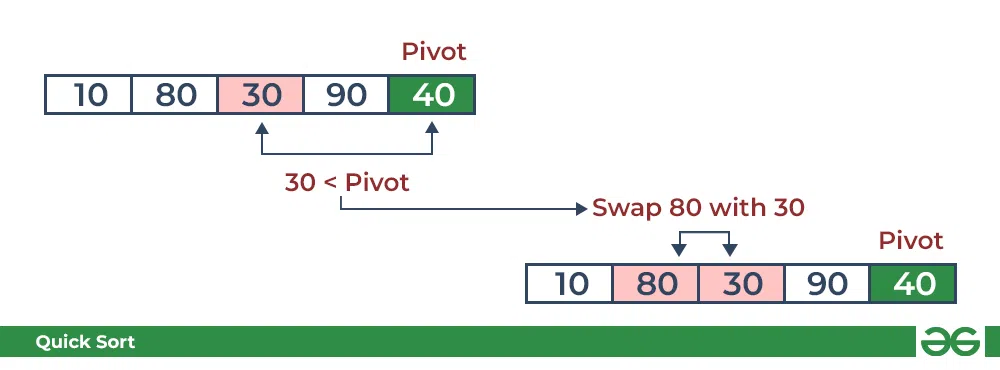
- Compare 30 with pivot. It is less than pivot so arrange it accordingly.
Partition in QuickSort: Compare pivot with 30
- Compare 90 with the pivot. It is greater than the pivot.
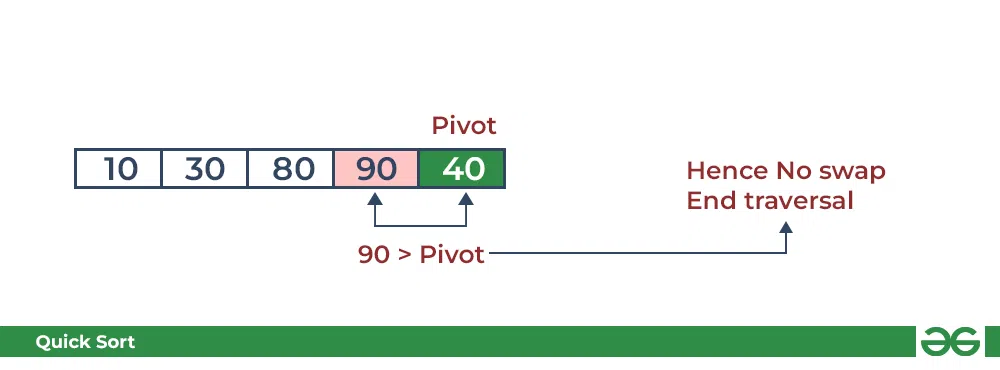
Partition in QuickSort: Compare pivot with 90
- Arrange the pivot in its correct position.
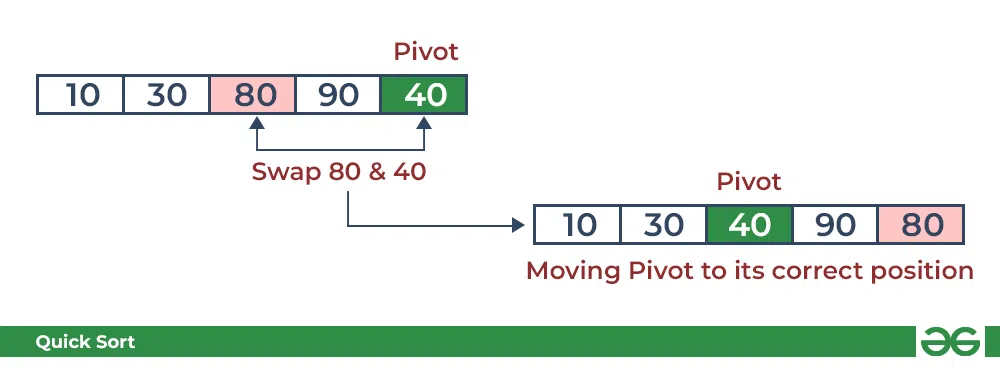
Partition in QuickSort: Place pivot in its correct position
Illustration of Quicksort:
As the partition process is done recursively, it keeps on putting the pivot in its actual position in the sorted array. Repeatedly putting pivots in their actual position makes the array sorted.
Follow the below images to understand how the recursive implementation of the partition algorithm helps to sort the array.
- Initial partition on the main array:
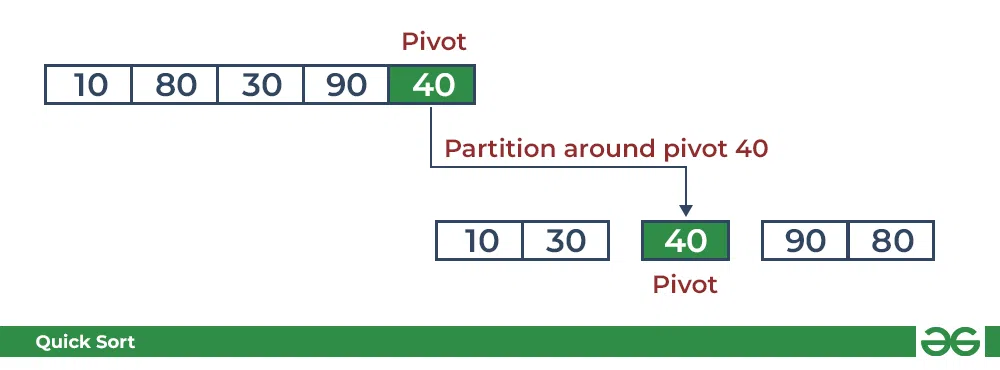
Quicksort: Performing the partition
- Partitioning of the subarrays:

Quicksort: Performing the partition
Code implementation of the Quick Sort:
C++
#include <bits/stdc++.h>
using namespace std;
int partition(int arr[],int low,int high)
{
//choose the pivot
int pivot=arr[high];
//Index of smaller element and Indicate
//the right position of pivot found so far
int i=(low-1);
for(int j=low;j<=high;j++)
{
//If current element is smaller than the pivot
if(arr[j]<pivot)
{
//Increment index of smaller element
i++;
swap(arr[i],arr[j]);
}
}
swap(arr[i+1],arr[high]);
return (i+1);
}
// The Quicksort function Implement
void quickSort(int arr[],int low,int high)
{
// when low is less than high
if(low<high)
{
// pi is the partition return index of pivot
int pi=partition(arr,low,high);
//Recursion Call
//smaller element than pivot goes left and
//higher element goes right
quickSort(arr,low,pi-1);
quickSort(arr,pi+1,high);
}
}
int main() {
int arr[]={10,7,8,9,1,5};
int n=sizeof(arr)/sizeof(arr[0]);
// Function call
quickSort(arr,0,n-1);
//Print the sorted array
cout<<"Sorted Array\n";
for(int i=0;i<n;i++)
{
cout<<arr[i]<<" ";
}
return 0;
}
// This Code is Contributed By Diwakar Jha
// C program for QuickSort
#include <stdio.h>
// Utility function to swap tp integers
void swap(int* p1, int* p2)
{
int temp;
temp = *p1;
*p1 = *p2;
*p2 = temp;
}
int partition(int arr[], int low, int high)
{
// choose the pivot
int pivot = arr[high];
// Index of smaller element and Indicate
// the right position of pivot found so far
int i = (low - 1);
for (int j = low; j <= high; j++) {
// If current element is smaller than the pivot
if (arr[j] < pivot) {
// Increment index of smaller element
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
// The Quicksort function Implement
void quickSort(int arr[], int low, int high)
{
// when low is less than high
if (low < high) {
// pi is the partition return index of pivot
int pi = partition(arr, low, high);
// Recursion Call
// smaller element than pivot goes left and
// higher element goes right
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
int main()
{
int arr[] = { 10, 7, 8, 9, 1, 5 };
int n = sizeof(arr) / sizeof(arr[0]);
// Function call
quickSort(arr, 0, n - 1);
// Print the sorted array
printf("Sorted Array\n");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
return 0;
}
// This Code is Contributed By Diwakar Jha
// Java implementation of QuickSort
import java.io.*;
class GFG {
// A utility function to swap two elements
static void swap(int[] arr, int i, int j)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
// This function takes last element as pivot,
// places the pivot element at its correct position
// in sorted array, and places all smaller to left
// of pivot and all greater elements to right of pivot
static int partition(int[] arr, int low, int high)
{
// Choosing the pivot
int pivot = arr[high];
// Index of smaller element and indicates
// the right position of pivot found so far
int i = (low - 1);
for (int j = low; j <= high - 1; j++) {
// If current element is smaller than the pivot
if (arr[j] < pivot) {
// Increment index of smaller element
i++;
swap(arr, i, j);
}
}
swap(arr, i + 1, high);
return (i + 1);
}
// The main function that implements QuickSort
// arr[] --> Array to be sorted,
// low --> Starting index,
// high --> Ending index
static void quickSort(int[] arr, int low, int high)
{
if (low < high) {
// pi is partitioning index, arr[p]
// is now at right place
int pi = partition(arr, low, high);
// Separately sort elements before
// partition and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
// To print sorted array
public static void printArr(int[] arr)
{
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
// Driver Code
public static void main(String[] args)
{
int[] arr = { 10, 7, 8, 9, 1, 5 };
int N = arr.length;
// Function call
quickSort(arr, 0, N - 1);
System.out.println("Sorted array:");
printArr(arr);
}
}
// This code is contributed by Ayush Choudhary
// Improved by Ajay Virmoti
# Python3 implementation of QuickSort
# Function to find the partition position
def partition(array, low, high):
# Choose the rightmost element as pivot
pivot = array[high]
# Pointer for greater element
i = low - 1
# Traverse through all elements
# compare each element with pivot
for j in range(low, high):
if array[j] <= pivot:
# If element smaller than pivot is found
# swap it with the greater element pointed by i
i = i + 1
# Swapping element at i with element at j
(array[i], array[j]) = (array[j], array[i])
# Swap the pivot element with
# the greater element specified by i
(array[i + 1], array[high]) = (array[high], array[i + 1])
# Return the position from where partition is done
return i + 1
# Function to perform quicksort
def quicksort(array, low, high):
if low < high:
# Find pivot element such that
# element smaller than pivot are on the left
# element greater than pivot are on the right
pi = partition(array, low, high)
# Recursive call on the left of pivot
quicksort(array, low, pi - 1)
# Recursive call on the right of pivot
quicksort(array, pi + 1, high)
# Driver code
if __name__ == '__main__':
array = [10, 7, 8, 9, 1, 5]
N = len(array)
# Function call
quicksort(array, 0, N - 1)
print('Sorted array:')
for x in array:
print(x, end=" ")
# This code is contributed by Adnan Aliakbar
// C# implementation of QuickSort
using System;
class GFG {
// A utility function to swap two elements
static void swap(int[] arr, int i, int j)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
// This function takes last element as pivot,
// places the pivot element at its correct position
// in sorted array, and places all smaller to left
// of pivot and all greater elements to right of pivot
static int partition(int[] arr, int low, int high)
{
// Choosing the pivot
int pivot = arr[high];
// Index of smaller element and indicates
// the right position of pivot found so far
int i = (low - 1);
for (int j = low; j <= high - 1; j++) {
// If current element is smaller than the pivot
if (arr[j] < pivot) {
// Increment index of smaller element
i++;
swap(arr, i, j);
}
}
swap(arr, i + 1, high);
return (i + 1);
}
// The main function that implements QuickSort
// arr[] --> Array to be sorted,
// low --> Starting index,
// high --> Ending index
static void quickSort(int[] arr, int low, int high)
{
if (low < high) {
// pi is partitioning index, arr[p]
// is now at right place
int pi = partition(arr, low, high);
// Separately sort elements before
// and after partition index
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
// Driver Code
public static void Main()
{
int[] arr = { 10, 7, 8, 9, 1, 5 };
int N = arr.Length;
// Function call
quickSort(arr, 0, N - 1);
Console.WriteLine("Sorted array:");
for (int i = 0; i < N; i++)
Console.Write(arr[i] + " ");
}
}
// This code is contributed by gfgking
// Function to partition the array and return the partition index
function partition(arr, low, high) {
// Choosing the pivot
let pivot = arr[high];
// Index of smaller element and indicates the right position of pivot found so far
let i = low - 1;
for (let j = low; j <= high - 1; j++) {
// If current element is smaller than the pivot
if (arr[j] < pivot) {
// Increment index of smaller element
i++;
[arr[i], arr[j]] = [arr[j], arr[i]]; // Swap elements
}
}
[arr[i + 1], arr[high]] = [arr[high], arr[i + 1]]; // Swap pivot to its correct position
return i + 1; // Return the partition index
}
// The main function that implements QuickSort
function quickSort(arr, low, high) {
if (low < high) {
// pi is the partitioning index, arr[pi] is now at the right place
let pi = partition(arr, low, high);
// Separately sort elements before partition and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
// Driver code
let arr = [10, 7, 8, 9, 1, 5];
let N = arr.length;
// Function call
quickSort(arr, 0, N - 1);
console.log("Sorted array:");
console.log(arr.join(" "));
<?php
// code
?>
<?php
// This Function takes place last element as pivot
// Place the pivot as correct position
// In Sorted Array, and places all smaller to left
// of pivot and all greater element to its right of pivot
function partition(&$arr,$low,$high)
{
// Choose the Pivot Element
$pivot= $arr[$high];
// Index of smaller element and indicates
// The right position of pivot
$i=($low-1);
for($j=$low;$j<=$high-1;$j++)
{
if($arr[$j]<$pivot)
{
// Increment index of smaller element
$i++;
list($arr[$i],$arr[$j])=array($arr[$j],$arr[$i]);
}
}
// Pivot element as correct position
list($arr[$i+1],$arr[$high])=array($arr[$high],$arr[$i+1]);
return ($i+1);
}
// The main function that implement as QuickSort
// arr[]:- Array to be sorted
// low:- Starting Index
//high:- Ending Index
function quickSort(&$arr,$low,$high)
{
if($low<$high)
{
// pi is partition
$pi= partition($arr,$low,$high);
// Sort the array
// Before the partition of Element
quickSort($arr,$low,$pi-1);
// After the partition Element
quickSort($arr,$pi+1,$high);
}
}
// Driver Code
$arr= array(10,7,8,9,1,5);
$N=count($arr);
// Function Call
quickSort($arr,0,$N-1);
echo "Sorted Array:\n";
for($i=0;$i<$N;$i++)
{
echo $arr[$i]. " ";
}
//This code is contributed by Diwakar Jha
OutputSorted Array
1 5 7 8 9 10
Time Complexity:
- Best Case: Ω (N log (N))
The best-case scenario for quicksort occur when the pivot chosen at the each step divides the array into roughly equal halves.
In this case, the algorithm will make balanced partitions, leading to efficient Sorting. - Average Case: θ ( N log (N))
Quicksort’s average-case performance is usually very good in practice, making it one of the fastest sorting Algorithm. - Worst Case: O(N2)
The worst-case Scenario for Quicksort occur when the pivot at each step consistently results in highly unbalanced partitions. When the array is already sorted and the pivot is always chosen as the smallest or largest element. To mitigate the worst-case Scenario, various techniques are used such as choosing a good pivot (e.g., median of three) and using Randomized algorithm (Randomized Quicksort ) to shuffle the element before sorting. - Auxiliary Space: O(1), if we don’t consider the recursive stack space. If we consider the recursive stack space then, in the worst case quicksort could make O(N).
Advantages of Quick Sort:
- It is a divide-and-conquer algorithm that makes it easier to solve problems.
- It is efficient on large data sets.
- It has a low overhead, as it only requires a small amount of memory to function.
Disadvantages of Quick Sort:
- It has a worst-case time complexity of O(N2), which occurs when the pivot is chosen poorly.
- It is not a good choice for small data sets.
- It is not a stable sort, meaning that if two elements have the same key, their relative order will not be preserved in the sorted output in case of quick sort, because here we are swapping elements according to the pivot’s position (without considering their original positions).
Share your thoughts in the comments
Please Login to comment...