In this article, we are going to discuss how Divide and Conquer technique is helpful and how we can solve the problem with the DAC technique approach. In this section, we will discuss the following topics.
1. Introduction to DAC.
2. Algorithms under DAC techniques.
3. Recurrence Relation for DAC algorithm.
4. Problems using DAC technique.
Divide And Conquer
This technique can be divided into the following three parts:
- Divide: This involves dividing the problem into smaller sub-problems.
- Conquer: Solve sub-problems by calling recursively until solved.
- Combine: Combine the sub-problems to get the final solution of the whole problem.
The following are some standard algorithms that follow Divide and Conquer algorithm.
- Quicksort is a sorting algorithm. The algorithm picks a pivot element and rearranges the array elements so that all elements smaller than the picked pivot element move to the left side of the pivot, and all greater elements move to the right side. Finally, the algorithm recursively sorts the subarrays on the left and right of the pivot element.
- Merge Sort is also a sorting algorithm. The algorithm divides the array into two halves, recursively sorts them, and finally merges the two sorted halves.
- Closest Pair of Points The problem is to find the closest pair of points in a set of points in the x-y plane. The problem can be solved in O(n^2) time by calculating the distances of every pair of points and comparing the distances to find the minimum. The Divide and Conquer algorithm solves the problem in O(N log N) time.
- Strassen’s Algorithm is an efficient algorithm to multiply two matrices. A simple method to multiply two matrices needs 3 nested loops and is O(n^3). Strassen’s algorithm multiplies two matrices in O(n^2.8974) time.
- Cooley–Tukey Fast Fourier Transform (FFT) algorithm is the most common algorithm for FFT. It is a divide and conquer algorithm which works in O(N log N) time.
- Karatsuba algorithm for fast multiplication does the multiplication of two n-digit numbers in at most
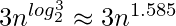
single-digit multiplications in general (and exactly 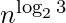 when n is a power of 2). It is, therefore, faster than the classical algorithm, which requires n2 single-digit products. If n = 210 = 1024, in particular, the exact counts are 310 = 59, 049 and (210)2 = 1, 048, 576, respectively.
when n is a power of 2). It is, therefore, faster than the classical algorithm, which requires n2 single-digit products. If n = 210 = 1024, in particular, the exact counts are 310 = 59, 049 and (210)2 = 1, 048, 576, respectively.
What does not qualifies as Divide and Conquer:
Binary Search is a searching algorithm. In each step, the algorithm compares the input element x with the value of the middle element in the array. If the values match, return the index of the middle. Otherwise, if x is less than the middle element, then the algorithm recurs for the left side of the middle element, else recurs for the right side of the middle element. Contrary to popular belief, this is not an example of Divide and Conquer because there is only one sub-problem in each step (Divide and conquer requires that there must be two or more sub-problems) and hence this is a case of Decrease and Conquer.
Divide And Conquer algorithm :
DAC(a, i, j)
{
if(small(a, i, j))
return(Solution(a, i, j))
else
mid = divide(a, i, j) // f1(n)
b = DAC(a, i, mid) // T(n/2)
c = DAC(a, mid+1, j) // T(n/2)
d = combine(b, c) // f2(n)
return(d)
}
Recurrence Relation for DAC algorithm :
This is a recurrence relation for the above program.
O(1) if n is small
T(n) = f1(n) + 2T(n/2) + f2(n)
Example:
To find the maximum and minimum element in a given array.
Input: { 70, 250, 50, 80, 140, 12, 14 }
Output: The minimum number in a given array is : 12
The maximum number in a given array is : 250Approach: To find the maximum and minimum element from a given array is an application for divide and conquer. In this problem, we will find the maximum and minimum elements in a given array. In this problem, we are using a divide and conquer approach(DAC) which has three steps divide, conquer and combine.
For Maximum:
In this problem, we are using the recursive approach to find the maximum where we will see that only two elements are left and then we can easily use condition i.e. if(a[index]>a[index+1].)
In a program line a[index] and a[index+1])condition will ensure only two elements in left.
if(index >= l-2)
{
if(a[index]>a[index+1])
{
// (a[index]
// Now, we can say that the last element will be maximum in a given array.
}
else
{
//(a[index+1]
// Now, we can say that last element will be maximum in a given array.
}
}
In the above condition, we have checked the left side condition to find out the maximum. Now, we will see the right side condition to find the maximum.
Recursive function to check the right side at the current index of an array.
max = DAC_Max(a, index+1, l);
// Recursive call
Now, we will compare the condition and check the right side at the current index of a given array.
In the given program, we are going to implement this logic to check the condition on the right side at the current index.
// Right element will be maximum.
if(a[index]>max)
return a[index];
// max will be maximum element in a given array.
else
return max;
}
For Minimum:
In this problem, we are going to implement the recursive approach to find the minimum no. in a given array.
int DAC_Min(int a[], int index, int l)
//Recursive call function to find the minimum no. in a given array.
if(index >= l-2)
// to check the condition that there will be two-element in the left
then we can easily find the minimum element in a given array.
{
// here we will check the condition
if(a[index]<a[index+1])
return a[index];
else
return a[index+1];
}
Now, we will check the condition on the right side in a given array.
// Recursive call for the right side in the given array.
min = DAC_Min(a, index+1, l);
Now, we will check the condition to find the minimum on the right side.
// Right element will be minimum
if(a[index]<min)
return a[index];
// Here min will be minimum in a given array.
else
return min;
Implementation:
C++
// C++ code to demonstrate Divide and
// Conquer Algorithm#include<iostream>
# include<iostream>
using namespace std;
// function to find the maximum no.
// in a given array.
int DAC_Max(int a[], int index, int l)
{
int max;
if(l - 1 == 0)
{
return a[index];
}
if(index >= l - 2)
{
if(a[index] > a[index + 1])
return a[index];
else
return a[index + 1];
}
max = DAC_Max(a, index + 1, l);
if(a[index] > max)
return a[index];
else
return max;
}
// Function to find the minimum no.
// in a given array
int DAC_Min(int a[], int index, int l)
{
int min;
if(l - 1 == 0)
{
return a[index];
}
if(index >= l - 2)
{
if(a[index] < a[index + 1])
return a[index];
else
return a[index + 1];
}
min = DAC_Min(a, index + 1, l);
if(a[index] < min)
return a[index];
else
return min;
}
// Driver code
int main()
{
int a[7] = { 70, 250, 50, 80, 140, 12, 14 };
int n = sizeof(a) / sizeof(a[0]);
int max, min;
max = DAC_Max(a, 0, n);
min = DAC_Min(a, 0, n);
cout << "The minimum number in a given array is : " << min << endl;
cout << "The maximum number in a given array is : " << max << endl;
return 0;
}
// This code is contributed by probinsah.
// C code to demonstrate Divide and
// Conquer Algorithm
#include <stdio.h>
int DAC_Max(int a[], int index, int l);
int DAC_Min(int a[], int index, int l);
// function to find the maximum no.
// in a given array.
int DAC_Max(int a[], int index, int l)
{
int max;
if(l - 1 == 0)
{
return a[index];
}
if (index >= l - 2) {
if (a[index] > a[index + 1])
return a[index];
else
return a[index + 1];
}
// logic to find the Maximum element
// in the given array.
max = DAC_Max(a, index + 1, l);
if (a[index] > max)
return a[index];
else
return max;
}
// Function to find the minimum no.
// in a given array.
int DAC_Min(int a[], int index, int l)
{
int min;
if(l - 1 == 0)
{
return a[index];
}
if (index >= l - 2) {
if (a[index] < a[index + 1])
return a[index];
else
return a[index + 1];
}
// Logic to find the Minimum element
// in the given array.
min = DAC_Min(a, index + 1, l);
if (a[index] < min)
return a[index];
else
return min;
}
// Driver Code
int main()
{
// Defining the variables
int min, max, N;
// Initializing the array
int a[7] = { 70, 250, 50, 80, 140, 12, 14 };
// recursion - DAC_Max function called
max = DAC_Max(a, 0, 7);
// recursion - DAC_Max function called
min = DAC_Min(a, 0, 7);
printf("The minimum number in a given array is : %d\n", min);
printf("The maximum number in a given array is : %d", max);
return 0;
}
// This code is contributed by Ashish Rana (GFG Team)
// Java code to demonstrate Divide and
// Conquer Algorithm
class GFG{
// Function to find the maximum no.
// in a given array.
static int DAC_Max(int a[], int index, int l)
{
int max;
if(l - 1 == 0)
{
return a[index];
}
if (index >= l - 2)
{
if (a[index] > a[index + 1])
return a[index];
else
return a[index + 1];
}
// Logic to find the Maximum element
// in the given array.
max = DAC_Max(a, index + 1, l);
if (a[index] > max)
return a[index];
else
return max;
}
// Function to find the minimum no.
// in a given array.
static int DAC_Min(int a[], int index, int l)
{
int min;
if(l - 1 == 0)
{
return a[index];
}
if (index >= l - 2)
{
if (a[index] < a[index + 1])
return a[index];
else
return a[index + 1];
}
// Logic to find the Minimum element
// in the given array.
min = DAC_Min(a, index + 1, l);
if (a[index] < min)
return a[index];
else
return min;
}
// Driver Code
public static void main(String[] args)
{
// Defining the variables
int min, max;
// Initializing the array
int a[] = { 70, 250, 50, 80, 140, 12, 14 };
// Recursion - DAC_Max function called
max = DAC_Max(a, 0, 7);
// Recursion - DAC_Max function called
min = DAC_Min(a, 0, 7);
System.out.printf("The minimum number in " +
"a given array is : %d\n", min);
System.out.printf("The maximum number in " +
"a given array is : %d", max);
}
}
// This code is contributed by Princi Singh
# Python3 code to demonstrate Divide and
# Conquer Algorithm
# Function to find the maximum no.
# in a given array.
def DAC_Max(a, index, l):
max = -1
if(l - 1 == 0):
return a[index]
if (index >= l - 2):
if (a[index] > a[index + 1]):
return a[index]
else:
return a[index + 1]
# Logic to find the Maximum element
# in the given array.
max = DAC_Max(a, index + 1, l)
if (a[index] > max):
return a[index]
else:
return max
# Function to find the minimum no.
# in a given array.
def DAC_Min(a, index, l):
min = 0
if(l - 1 == 0):
return a[index]
if (index >= l - 2):
if (a[index] < a[index + 1]):
return a[index]
else:
return a[index + 1]
# Logic to find the Minimum element
# in the given array.
min = DAC_Min(a, index + 1, l)
if (a[index] < min):
return a[index]
else:
return min
# Driver Code
if __name__ == '__main__':
# Defining the variables
min, max = 0, -1
# Initializing the array
a = [70, 250, 50, 80, 140, 12, 14]
# Recursion - DAC_Max function called
max = DAC_Max(a, 0, 7)
# Recursion - DAC_Max function called
min = DAC_Min(a, 0, 7)
print("The minimum number in a given array is : ", min)
print("The maximum number in a given array is : ", max)
# This code is contributed by 29AjayKumar
// C# code to demonstrate Divide and
// Conquer Algorithm
using System;
class GFG
{
// Function to find the maximum no.
// in a given array.
static int DAC_Max(int []a, int index, int l)
{
int max;
if(l - 1 == 0)
{
return a[index];
}
if (index >= l - 2)
{
if (a[index] > a[index + 1])
return a[index];
else
return a[index + 1];
}
// Logic to find the Maximum element
// in the given array.
max = DAC_Max(a, index + 1, l);
if (a[index] > max)
return a[index];
else
return max;
}
// Function to find the minimum no.
// in a given array.
static int DAC_Min(int []a, int index, int l)
{
int min;
if(l - 1 == 0)
{
return a[index];
}
if (index >= l - 2)
{
if (a[index] < a[index + 1])
return a[index];
else
return a[index + 1];
}
// Logic to find the Minimum element
// in the given array.
min = DAC_Min(a, index + 1, l);
if (a[index] < min)
return a[index];
else
return min;
}
// Driver Code
public static void Main(String[] args)
{
// Defining the variables
int min, max;
// Initializing the array
int []a = {70, 250, 50, 80, 140, 12, 14};
// Recursion - DAC_Max function called
max = DAC_Max(a, 0, 7);
// Recursion - DAC_Max function called
min = DAC_Min(a, 0, 7);
Console.Write("The minimum number in " +
"a given array is : {0}\n", min);
Console.Write("The maximum number in " +
"a given array is : {0}", max);
}
}
// This code contributed by shikhasingrajput
<script>
// Javascript code to demonstrate Divide and
// Conquer Algorithm
// Function to find the maximum no.
// in a given array.
function DAC_Max(a,index,l)
{
let max;
if(l - 1 == 0)
{
return arr[index];
}
if (index >= l - 2)
{
if (a[index] > a[index + 1])
return a[index];
else
return a[index + 1];
}
// Logic to find the Maximum element
// in the given array.
max = DAC_Max(a, index + 1, l);
if (a[index] > max)
return a[index];
else
return max;
}
// Function to find the minimum no.
// in a given array.
function DAC_Min(a,index,l)
{
let min;
if(l - 1 == 0)
{
return arr[index];
}
if (index >= l - 2)
{
if (a[index] < a[index + 1])
return a[index];
else
return a[index + 1];
}
// Logic to find the Minimum element
// in the given array.
min = DAC_Min(a, index + 1, l);
if (a[index] < min)
return a[index];
else
return min;
}
// Driver Code
let min, max;
let a=[70, 250, 50, 80, 140, 12, 14];
// Recursion - DAC_Max function called
max = DAC_Max(a, 0, 7);
// Recursion - DAC_Max function called
min = DAC_Min(a, 0, 7);
document.write("The minimum number in " +
"a given array is : ", min+"<br>");
document.write("The maximum number in " +
"a given array is : "+ max+"<br>");
// This code is contributed by rag2127
</script>
OutputThe minimum number in a given array is : 12
The maximum number in a given array is : 250
Time Complexity:
The time complexity of the divide and conquer algorithm to find the maximum and minimum element in an array is O(n). This is because each time we divide the array in half, so we will have a total of log(n) divisions. In each division, we compare two elements to find the maximum and minimum element, which takes constant time. Therefore, the total time complexity is O(n*log(n)).
Space Complexity:
The space complexity of the divide and conquer algorithm to find the maximum and minimum element in an array is O(log(n)). This is because we are using recursion to divide the array into smaller parts, and each recursive call takes up space on the call stack. The maximum depth of the recursion tree is log(n), which is the number of times we can divide the array in half. Therefore, the space complexity is O(log(n)).
Divide and Conquer (D & C) vs Dynamic Programming (DP)
Both paradigms (D & C and DP) divide the given problem into subproblems and solve subproblems. How do choose one of them for a given problem? Divide and Conquer should be used when the same subproblems are not evaluated many times. Otherwise Dynamic Programming or Memoization should be used. For example, Quicksort is a Divide and Conquer algorithm, we never evaluate the same subproblems again. On the other hand, for calculating the nth Fibonacci number, Dynamic Programming should be preferred (See this for details).
Time Complexity of Divide and Conquer Algorithm:
T(n) = aT(n/b) + f(n),
where,
n = size of input
a = number of subproblems in the recursion
n/b = size of each subproblem. All subproblems are assumed to have the same size.
f(n) = cost of the work done outside the recursive call,
which includes the cost of dividing the problem and cost of merging the solutions
Advantages of Divide and Conquer Algorithm:
- The difficult problem can be solved easily.
- It divides the entire problem into subproblems thus it can be solved parallelly ensuring multiprocessing
- Efficiently uses cache memory without occupying much space
- Reduces time complexity of the problem
- Solving difficult problems: Divide and conquer technique is a tool for solving difficult problems conceptually. e.g. Tower of Hanoi puzzle. It requires a way of breaking the problem into sub-problems, and solving all of them as an individual cases and then combining sub- problems to the original problem.
- Algorithm efficiency: The divide-and-conquer paradigm often helps in the discovery of efficient algorithms. It was the key, for example to the Quicksort and Mergesort algorithms, and fast Fourier transforms. In all these examples, the D and C approach led to an improvement in the asymptotic cost of the solution. In particular, if the base cases have constant-bounded size, the work of splitting the problem and combining the partial solutions is proportional to the problem’s size n, and there are a bounded number p of subproblems of size-n/p at each stage, then the cost of the divide-and-conquer algorithm will be O(n log n).
- Parallelism: Normally DAC algorithms are used in multi-processor machines having shared-memory systems where the communication of data between processors does not need to be planned in advance, because distinct sub-problems can be executed on different processors.
- Memory access: These algorithms naturally make an efficient use of memory caches. Since the subproblems are small enough to be solved in cache without using the main memory that is slower one. Any algorithm that uses cache efficiently is called cache oblivious.
- Roundoff control: In computations with rounded arithmetic, e.g. with floating point numbers, a divide-and-conquer algorithm may yield more accurate results than a superficially equivalent iterative method. For example, one can add N numbers either by a simple loop that adds each datum to a single variable, or by a D And C algorithm that breaks the data set into two halves, recursively computes the sum of each half, and then adds the two sums. While the second method performs the same number of additions as the first, and pays the overhead of the recursive calls, it is usually more accurate.
Disadvantages of Divide and Conquer Algorithm:
- It involves recursion which is sometimes slow
- Efficiency depends on the implementation of logic
- It may crash the system if the recursion is performed rigorously.
- Overhead: The process of dividing the problem into subproblems and then combining the solutions can require additional time and resources. This overhead can be significant for problems that are already relatively small or that have a simple solution.
- Complexity: Dividing a problem into smaller subproblems can increase the complexity of the overall solution. This is particularly true when the subproblems are interdependent and must be solved in a specific order.
- Difficulty of implementation: Some problems are difficult to divide into smaller subproblems or require a complex algorithm to do so. In these cases, it can be challenging to implement a divide and conquer solution.
- Memory limitations: When working with large data sets, the memory requirements for storing the intermediate results of the subproblems can become a limiting factor.
- Suboptimal solutions: Depending on how the subproblems are defined and how they are combined, a divide and conquer solution may not always produce the most optimal solution. In some cases, it may be necessary to apply additional optimization techniques to improve the final solution.
- Difficulty in parallelization: In some cases, dividing the problem into subproblems and solving them independently may not be easily parallelizable, leading to inefficient use of computational resources.
Divide and Conquer is a popular algorithmic technique in computer science that involves breaking down a problem into smaller sub-problems, solving each sub-problem independently, and then combining the solutions to the sub-problems to solve the original problem. The basic idea behind this technique is to divide a problem into smaller, more manageable sub-problems that can be solved more easily.
The divide and conquer algorithm typically consists of three steps:
- Divide: The problem is divided into smaller sub-problems that are similar to the original problem but of smaller size. The division is done until the sub-problems become small enough to be solved directly.
- Conquer: The sub-problems are solved recursively using the same algorithm until they become simple enough to be solved directly.
- Combine: The solutions to the sub-problems are combined to solve the original problem.
- This technique is used in many algorithms, including quicksort, mergesort, binary search, and Karatsuba’s algorithm for multiplying large integers.
The advantages of using the divide and conquer algorithm are:
- It is easy to implement and understand.
- It reduces the time complexity of the algorithm by breaking down the problem into smaller sub-problems.
- It can be used to solve a wide range of problems, including sorting, searching, and optimization.
- It can be used in parallel computing to improve performance.
The disadvantages of using the divide and conquer algorithm are:
- It can be difficult to determine the base case or stopping condition for the recursive calls.
- It may not be the most efficient algorithm for all problems.
- It may require more memory than other algorithms because it involves storing intermediate results.
Applications
- Merge Sort and Quicksort
- Median Finding
- Min and Max finding
- Matrix Multiplication
- Closest Pair problem
Reference books on divide and conquer algorithms:
“Introduction to Algorithms” by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein.
“Algorithms” by Sanjoy Dasgupta, Christos Papadimitriou, and Umesh Vazirani.
“The Art of Computer Programming, Volume 1: Fundamental Algorithms” by Donald E. Knuth.
References:
Algorithms by Sanjoy Dasgupta, Christos Papadimitriou, Umesh Vazirani
Introduction to Algorithms by Clifford Stein, Thomas H. Cormen, Charles E. Leiserson, Ronald L.
http://en.wikipedia.org/wiki/Karatsuba_algorithm
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...