Find the number of stair steps
Last Updated :
29 Sep, 2022
Given the total number of bricks T, find the number of stair steps that can be formed by using given bricks such that if step S has bricks B, then step S+1 should have exactly B+1 bricks and total number of bricks used should be less than or equal to number of bricks available.
Note: Number of bricks required to make step 1 of stair is 2, i.e step S = 1 must have exactly B = 2 bricks.
Examples:
Input: 15
Output: 4
Bricks should be arranged in this pattern to solve for T = 15:
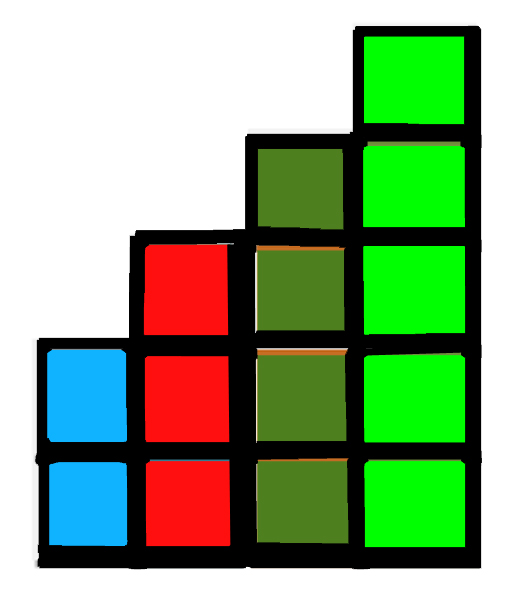
Explanation:
Number of bricks at step increases by one.
At Step 1, Number of bricks = 2, Total = 2
At step 2, Number of bricks = 3, Total = 5
At step 3, Number of bricks = 4, Total = 9
At step 4, Number of bricks = 5, Total = 14
If we add 6 more bricks to form new step,
then the total number of bricks available will surpass.
Hence, number of steps that can be formed are 4 and
number of bricks used are 14 and we are left with
1 brick which is useless.
Input : 40
Output : 7
Bricks should be arranged in this pattern to solve for T = 40:

Explanation:
At Step 1, Number of bricks = 2, Total = 2
At step 2, Number of bricks = 3, Total = 5
At step 3, Number of bricks = 4, Total = 9
At step 4, Number of bricks = 5, Total = 14
At step 5, Number of bricks = 6, Total = 20
At step 6, Number of bricks = 7, Total = 27
At step 7, Number of bricks = 8, Total = 35
If we add 9 more bricks to form new step,
then the total number of bricks available will surpass.
Hence, number of steps that can be formed are 7 and
number of bricks used are 35 and we are left with
5 bricks which are useless.
Approach:
We are interested in the number of steps and we know that each step Si uses exactly Bi number of bricks. We can represent this problem as an equation:
n * (n + 1) / 2 = T (For Natural number series starting from 1, 2, 3, 4, 5 …)
n * (n + 1) = 2 * T
n-1 will represent our final solution because our series in problem starts from 2, 3, 4, 5…
Now, we just have to solve this equation and for that we can exploit binary search to find the solution to this equation. Lower and Higher bounds of binary search are 1 and T.
Below is the implementation for the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int solve(int low, int high, int T)
{
while (low <= high) {
int mid = (low + high) / 2;
if ((mid * (mid + 1)) == T)
return mid;
if (mid > 0 && (mid * (mid + 1)) > T &&
(mid * (mid - 1)) <= T)
return mid - 1;
if ((mid * (mid + 1)) > T)
high = mid - 1;
else
low = mid + 1;
}
return -1;
}
int main()
{
int T = 15;
int ans = solve(1, T, 2 * T);
if (ans != -1)
ans--;
cout << "Number of stair steps = "
<< ans << endl;
return 0;
}
|
Java
import java.util.*;
import java.lang.*;
public class GfG {
public static int solve(int low, int high, int T)
{
while (low <= high) {
int mid = (low + high) / 2;
if ((mid * (mid + 1)) == T)
return mid;
if (mid > 0 && (mid * (mid + 1)) > T &&
(mid * (mid - 1)) <= T)
return mid - 1;
if ((mid * (mid + 1)) > T)
high = mid - 1;
else
low = mid + 1;
}
return -1;
}
public static void main(String argc[])
{
int T = 15;
int ans = solve(1, T, 2 * T);
if (ans != -1)
ans--;
System.out.println("Number of stair steps = " + ans);
}
}
|
Python3
def solve( low, high, T ):
while low <= high:
mid = int((low + high) / 2)
if (mid * (mid + 1)) == T:
return mid
if (mid > 0 and (mid * (mid + 1)) > T
and (mid * (mid - 1)) <= T) :
return mid - 1
if (mid * (mid + 1)) > T:
high = mid - 1;
else:
low = mid + 1
return -1
T = 15
ans = solve(1, T, 2 * T)
if ans != -1:
ans-= 1
print("Number of stair steps = ", ans)
|
C#
using System;
public class GfG {
public static int solve(int low, int high, int T)
{
while (low <= high) {
int mid = (low + high) / 2;
if ((mid * (mid + 1)) == T)
return mid;
if (mid > 0 && (mid * (mid + 1)) > T &&
(mid * (mid - 1)) <= T)
return mid - 1;
if ((mid * (mid + 1)) > T)
high = mid - 1;
else
low = mid + 1;
}
return -1;
}
public static void Main()
{
int T = 15;
int ans = solve(1, T, 2 * T);
if (ans != -1)
ans--;
Console.WriteLine("Number of stair steps = " + ans);
}
}
|
PHP
<?php
function solve($low, $high, $T)
{
while ($low <= $high)
{
$mid = ($low + $high) / 2;
if (($mid * ($mid + 1)) == $T)
return $mid;
if ($mid > 0 && ($mid * ($mid + 1)) > $T &&
($mid * ($mid - 1)) <= $T )
return $mid - 1;
if (($mid * ($mid + 1)) > $T)
$high = $mid - 1;
else
$low = $mid + 1;
}
return -1;
}
$T = 15;
$ans = solve(1, $T, 2 * $T);
if ($ans != -1)
$ans--;
echo "Number of stair steps = ", $ans, "\n";
?>
|
Javascript
<script>
function solve(low, high, T)
{
while (low <= high)
{
let mid = Math.floor((low + high) / 2);
if ((mid * (mid + 1)) == T)
return mid;
if (mid > 0 && (mid * (mid + 1)) > T &&
(mid * (mid - 1)) <= T)
return mid - 1;
if ((mid * (mid + 1)) > T)
high = mid - 1;
else
low = mid + 1;
}
return -1;
}
let T = 15;
let ans = solve(1, T, 2 * T);
if (ans != -1)
ans--;
document.write("Number of stair steps = " + ans);
</script>
|
Output:
Number of stair steps = 4
Time complexity: O(logT) for given input T
Auxiliary space: O(1)
Share your thoughts in the comments
Please Login to comment...