A child is running up a staircase with n steps and can hop either 1 step, 2 steps, or 3 steps at a time. Implement a method to count how many possible ways the child can run up the stairs.
Examples: 

Input : 4
Output : 7
Explantion:
Below are the four ways
 1 step + 1 step + 1 step + 1 step
 1 step + 2 step + 1 step
 2 step + 1 step + 1 step 
 1 step + 1 step + 2 step
 2 step + 2 step
 3 step + 1 step
 1 step + 3 step

Input : 3
Output : 4
Explantion:
Below are the four ways
 1 step + 1 step + 1 step
 1 step + 2 step
 2 step + 1 step
 3 step

There are two methods to solve this problem:  

1. Recursive Method
2. Dynamic Programming

Method 1: Recursive. 
There are n stairs, and a person is allowed to jump next stair, skip one stair or skip two stairs. So there are n stairs. So if a person is standing at i-th stair, the person can move to i+1, i+2, i+3-th stair. A recursive function can be formed where at current index i the function is recursively called for i+1, i+2 and i+3 th stair. 
There is another way of forming the recursive function. To reach a stair i, a person has to jump either from i-1, i-2 or i-3 th stair or i is the starting stair.
Algorithm: 

1. Create a recursive function (count(int n)) which takes only one parameter.
2. Check the base cases. If the value of n is less than 0 then return 0, and if the value of n is equal to zero then return 1 as it is the starting stair.
3. Call the function recursively with values n-1, n-2 and n-3 and sum up the values that are returned, i.e. sum = count(n-1) + count(n-2) + count(n-3)
4. Return the value of the sum.

Output : 

7

Working:

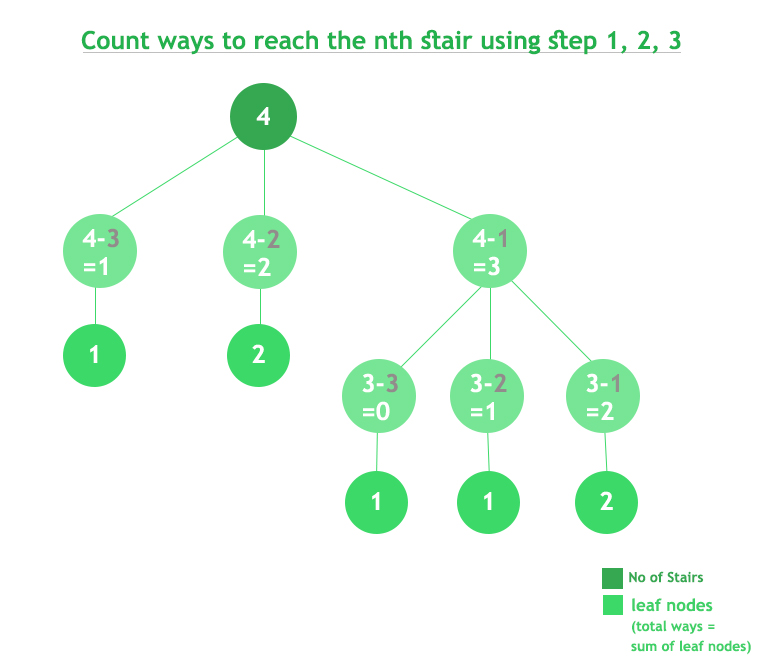
Complexity Analysis: 

• Time Complexity: O(3ⁿ). 
  The time complexity of the above solution is exponential, a close upper bound will be O(3ⁿ). From each state, 3 recursive function are called. So the upperbound for n states is O(3ⁿ).
• Space Complexity:O(1). 
  As no extra space is required.

Note: The Time Complexity of the program can be optimized using Dynamic Programming.
Method 2: Dynamic Programming.
The idea is similar, but it can be observed that there are n states but the recursive function is called 3 ^ n times. That means that some states are called repeatedly. So the idea is to store the value of states. This can be done in two ways.  

• Top-Down Approach: The first way is to keep the recursive structure intact and just store the value in a HashMap and whenever the function is called again return the value store without computing ().
• Bottom-Up Approach: The second way is to take an extra space of size n and start computing values of states from 1, 2 .. to n, i.e. compute values of i, i+1, i+2 and then use them to calculate the value of i+3.

Algorithm:  

1. Create an array of size n + 1 and initialize the first 3 variables with 1, 1, 2. The base cases.
2. Run a loop from 3 to n.
3. For each index i, computer value of ith position as dp[i] = dp[i-1] + dp[i-2] + dp[i-3].
4. Print the value of dp[n], as the Count of the number of ways to reach n th step.

Output : 
 

7

• Working:

1 -> 1 -> 1 -> 1
1 -> 1 -> 2
1 -> 2 -> 1
1 -> 3
2 -> 1 -> 1
2 -> 2
3 -> 1

So Total ways: 7

• Complexity Analysis: 
  • Time Complexity: O(n). 
    Only one traversal of the array is needed. So Time Complexity is O(n).
  • Space Complexity: O(n). 
    To store the values in a DP, n extra space is needed.

Method 3: Matrix Exponentiation (O(logn) Approach)

Matrix Exponentiation is mathematical ways to solve DP problem in better time complexity . Matrix Exponentiation Technique has Transformation matrix of Size K X K and Functional Vector (K X 1) .By taking n-1th power of Transformation matrix and Multiplying It With functional vector Give Resultant Vector say it  Res  of Size K X 1. First Element of Res will be Answer for given n value. This Approach Will Take O(K^3logn) Time Complexity Which Is Complexity of Finding (n-1) power of Transformation Matrix.

Key Terms:

K = No of Terms in which F(n) depend ,from Recurrence Relation We can Say That F(n) depend On F(n-1) and F(n-2). => K =3

F1 =  Vector (1D array) that contain F(n) value of First K terms. Since K=3 =>F1 will have F(n) value of first 2 terms. F1=[1,2,4]

T = Transformation Matrix that is a 2D matrix of Size K X K and  Consist Of All 1 After Diagonal And Rest All Zero except last row. Last Row Will have coefficient Of all K terms in which F(n)  depends In Reverser Order. => T =[ [0 1 0] ,[0 0 1], [1 1 1] ].

Algorithms:

1)Take Input N
2)If N < K then Return Precalculated Answer  //Base Condition
3)construct F1 Vector and T (Transformation Matrix)
4)Take N-1th  power of T by using  Optimal Power(T,N) Methods and assign it in T
5)return (TXF)[1]

for Optimal Power(T,N) Methods Refer Following Article : https://www.geeksforgeeks.org/write-a-c-program-to-calculate-powxn/

7
13
274

Explanation:
We Know For This Question 
Transformation Matrix M= [[0,1,0],[0,0,1],[1,1,1]]
Functional Vector F1 = [1,2,4]
for n=2 :
    ans = (M X F1)[1]  
    ans = [2,4,7][1]  
    ans = 2 //[2,4,7][1] = First cell value of [2,4,7] i.e 2
for n=3 :
    ans = (M X M X F1)[1]  //M^(3-1) X F1 = M X M X F1
    ans = (M X [2,4,7])[1] 
    ans = [4,7,13][1]
    ans = 4
for n = 4 :
    ans = (M^(4-1) X F1)[1]
    ans = (M X M X M X F1) [1] 
    ans = (M X [4,7,13])[1] 
    ans = [7,13,24][1]
    ans = 7
for n = 5 :
    ans = (M^4 X F1)[1]
    ans = (M X [7,13,24])[1]
    ans = [13,24,44][1]
    ans = 13

Time Complexity:

O(K^3log(n)) //For Computing pow(t,n-1)
For this question K is 3
So Overall Time Complexity is O(27log(n))=O(logn)

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready.  To complete your preparation from learning a language to DS Algo and many more,  please refer Complete Interview Preparation Course.

In case you wish to attend live classes with industry experts, please refer Geeks Classes Live