Find number of endless points
Last Updated :
13 Sep, 2023
Given a binary N x N matrix, we need to find the total number of matrix positions from which there is an endless path. Any position (i, j) is said to have an endless path if and only if the position (i, j) has the value 1 and all the next positions in its row(i) and its column(j) should have value 1. If any position next to (i, j) either in a row(i) or in column(j) will have 0 then position (i, j) doesn’t have any endless path.
Examples:
Input : 0 1 0
1 1 1
0 1 1
Output : 4
Endless points are (1, 1), (1, 2),
(2, 1) and (2, 2). For all other
points path to some corner is
blocked at some point.
Input : 0 1 1
1 1 0
0 1 0
Output : 1
Endless point is (0, 1).
Naive Approach :
We traverse all positions, for every position, we check that does this position has an endless path or not. If yes then count it otherwise ignore it. But as usual, its time complexity seems to be high.
Time complexity: O(n3)
Advance Approach (Dynamic programming):
We can easily say that if there is a zero at any position, then it will block the path for all the positions left to it and on top of it.
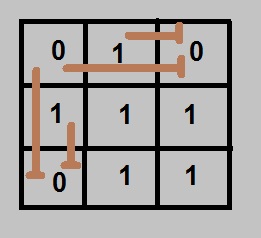
Also, we can say that any position (i,j) will have an endless row if (i,j+1) will have an endless row and the value of (i, j) is 1.
Similarly, we can say that any position (i,j) will have an endless column if (i+1,j) will have an endless column and the value of (i, j) is 1.
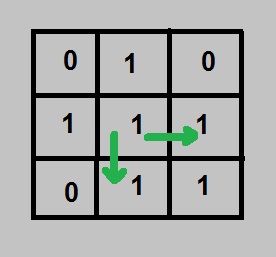
So we should maintain two matrices one for the row and one for the column. Always start from the rightmost position for row and bottom-most position for column and only check for next position whether it has an endless path or not.
And Finally, if any position will have an endless path in both row and column matrix then that position is said to have an endless path.
Implementation:
C++
#include<bits/stdc++.h>
using namespace std;
const int MAX = 100;
int countEndless(bool input[][MAX], int n)
{
bool row[n][n], col[n][n];
for (int j=0; j<n; j++)
{
bool isEndless = 1;
for (int i=n-1; i>=0; i--)
{
if (input[i][j] == 0)
isEndless = 0;
col[i][j] = isEndless;
}
}
for (int i=0; i<n; i++)
{
bool isEndless = 1;
for (int j= n-1; j>=0; j--)
{
if (input[i][j] == 0)
isEndless = 0;
row[i][j] = isEndless;
}
}
int ans = 0;
for (int i=0; i<n; i++)
for (int j=1; j<n; j++)
if (row[i][j] && col[i][j])
ans++;
return ans;
}
int main()
{
bool input[][MAX] = { {1, 0, 1, 1},
{0, 1, 1, 1},
{1, 1, 1, 1},
{0, 1, 1, 0}};
int n = 4;
cout << countEndless(input, n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static final int MAX = 100;
static int countEndless(boolean input[][], int n)
{
boolean row[][] = new boolean[n][n];
boolean col[][] = new boolean[n][n];
for (int j = 0; j < n; j++)
{
boolean isEndless = true;
for (int i = n-1; i >= 0; i--)
{
if (input[i][j] == false)
isEndless = false;
col[i][j] = isEndless;
}
}
for (int i = 0; i < n; i++)
{
boolean isEndless = true;
for (int j = n-1; j >= 0; j--)
{
if (input[i][j] == false)
isEndless = false;
row[i][j] = isEndless;
}
}
int ans = 0;
for (int i = 0; i < n; i++)
for (int j = 1; j < n; j++)
if (row[i][j] && col[i][j])
ans++;
return ans;
}
public static void main(String arg[])
{
boolean input[][] = {
{true, false, true, true},
{false, true, true, true},
{true, true, true, true},
{false, true, true, false}};
int n = 4;
System.out.print(countEndless(input, n));
}
}
|
Python3
import numpy as np
def countEndless(input_mat, n) :
row = np.zeros((n, n))
col = np.zeros((n, n))
for j in range(n) :
isEndless = 1
for i in range(n - 1, -1, -1) :
if (input_mat[i][j] == 0) :
isEndless = 0
col[i][j] = isEndless
for i in range(n) :
isEndless = 1
for j in range(n - 1, -1, -1) :
if (input_mat[i][j] == 0) :
isEndless = 0
row[i][j] = isEndless
ans = 0
for i in range(n) :
for j in range(1, n) :
if (row[i][j] and col[i][j]) :
ans += 1
return ans
if __name__ == "__main__" :
input_mat = [[1, 0, 1, 1],
[0, 1, 1, 1],
[1, 1, 1, 1],
[0, 1, 1, 0]]
n = 4
print(countEndless(input_mat, n))
|
C#
using System;
public class GFG {
static int countEndless(bool [,]input, int n)
{
bool [,]row = new bool[n,n];
bool [,]col = new bool[n,n];
for (int j = 0; j < n; j++)
{
bool isEndless = true;
for (int i = n - 1; i >= 0; i--)
{
if (input[i,j] == false)
isEndless = false;
col[i,j] = isEndless;
}
}
for (int i = 0; i < n; i++)
{
bool isEndless = true;
for (int j = n - 1; j >= 0; j--)
{
if (input[i,j] == false)
isEndless = false;
row[i,j] = isEndless;
}
}
int ans = 0;
for (int i = 0; i < n; i++)
for (int j = 1; j < n; j++)
if (row[i,j] && col[i,j])
ans++;
return ans;
}
public static void Main()
{
bool [,]input = {
{true, false, true, true},
{false, true, true, true},
{true, true, true, true},
{false, true, true, false}};
int n = 4;
Console.Write(countEndless(input, n));
}
}
|
PHP
<?php
function countEndless($input, $n)
{
for ($j = 0; $j < $n; $j++)
{
$isEndless = 1;
for ($i = $n - 1; $i >= 0; $i--)
{
if ($input[$i][$j] == 0)
$isEndless = 0;
$col[$i][$j] = $isEndless;
}
}
for ($i = 0; $i < $n; $i++)
{
$isEndless = 1;
for ($j = $n - 1; $j >= 0; $j--)
{
if ($input[$i][$j] == 0)
$isEndless = 0;
$row[$i][$j] = $isEndless;
}
}
$ans = 0;
for ($i = 0; $i < $n; $i++)
for ($j = 1; $j < $n; $j++)
if ($row[$i][$j] &&
$col[$i][$j])
$ans++;
return $ans;
}
$input = array(array(1, 0, 1, 1),
array(0, 1, 1, 1),
array(1, 1, 1, 1),
array(0, 1, 1, 0));
$n = 4;
echo countEndless($input, $n);
?>
|
Javascript
<script>
let MAX = 100;
function countEndless(input, n)
{
let row = new Array(n);
for (let i = 0; i < n; i++)
{
row[i] = new Array(n);
for (let j = 0; j < n; j++)
{
row[i][j] = false;
}
}
let col = new Array(n);
for (let i = 0; i < n; i++)
{
col[i] = new Array(n);
for (let j = 0; j < n; j++)
{
col[i][j] = false;
}
}
for (let j = 0; j < n; j++)
{
let isEndless = true;
for (let i = n-1; i >= 0; i--)
{
if (input[i][j] == false)
isEndless = false;
col[i][j] = isEndless;
}
}
for (let i = 0; i < n; i++)
{
let isEndless = true;
for (let j = n-1; j >= 0; j--)
{
if (input[i][j] == false)
isEndless = false;
row[i][j] = isEndless;
}
}
let ans = 0;
for (let i = 0; i < n; i++)
for (let j = 1; j < n; j++)
if (row[i][j] && col[i][j])
ans++;
return ans;
}
let input = [
[true, false, true, true],
[false, true, true, true],
[true, true, true, true],
[false, true, true, false]];
let n = 4;
document.write(countEndless(input, n));
</script>
|
Time Complexity : O(n2), where n is the size of the matrix.
Auxiliary Space: O(n2)
Share your thoughts in the comments
Please Login to comment...