The Number System is a way of representing numbers on the number line with the help of a set of Symbols and rules. All the Mathematical concepts and formulas are based on Number system. We have curated the importance of number system in this article below.
Number
A number refers to a word or symbol which represents a particular quantity. It is with the help of numbers only that multiple arithmetic operations are performed and we have been able to develop so much in the field of physics and mathematics. One cannot live their life without the usage of numbers, even for the most basic chores or tasks. Even the money exchanged for commodities is a certain value represented by numbers.
A bunch of numbers grouped together is used to assign a person as their contact number. such is the prominence of numerals in our lives. Hence, it is imperative to know more about the numbers and number systems, as has been discussed below.
Counting Numbers
Such a set of numbers as is used to count certain objects is called counting numbers. Such a set of numbers starts with 1(one) and goes on till infinity. One here represents a single object. For example, Mr. A had one pencil and one pen in his hand, or I ate one banana today. Adding up two counting numbers yields another counting number. These are used in real life for basic exchange, calculations, and operations.
The Number Zero
Zero is denoted by 0. It is used to depict nothing. In other words, if something has no value at all, it is assigned the number zero as a quantity. The number zero comes before all the counting numbers, and forms the set of ‘whole numbers’.
The different types of numbers in mathematics,
- Natural Numbers A set of numbers as is used to count certain objects are called natural numbers. Such a set of numbers starts with 1(one) and goes on till infinity. It is to be noted that natural numbers include only positive integers.
- Whole Numbers A set of numbers that includes all the positive integers and zero.
- Integers An integer is defined as such a whole number that can assume either positive, negative or no value at all.
- Real Numbers Such numbers which include both rational numbers and their irrational counterparts.
- Rational Numbers Such numbers can be expressed in the form of a fraction.
- Irrational Numbers Such numbers cannot be expressed as a fraction.
The following diagram depicts all kinds of numbers discussed so far,
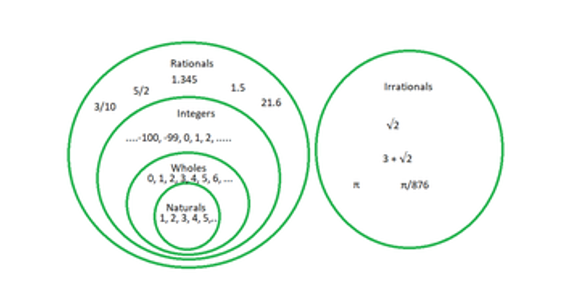
Apart from the above-mentioned types, we have the following categories of numbers as well,
- Even Numbers Such numbers as can be divided by 2 are called even numbers. Example: 2, 4, 6, 8, …, 1024, etc.
- Odd Numbers Such numbers as are not divisible by 2 are called odd numbers. Example: 3, 5, 7, 10, …, 1345, etc.
- Prime Numbers Such a number that can be divided exactly by itself or 1. Example: 5, 7, 13, 23, etc.
- Composite Numbers Such numbers as having multiple factors other than 1 and the number itself. Example: 16, 20, 50, etc.
Number System
It is clear that numbers are used to represent a certain quantity. When certain symbols or digits are used to represent the numbers themselves, it forms a number system. Hence, a number system is such a system as can be used to define a set of values, which are further used to represent a quantity.
Read More
Types of Number Systems
There are various types of number systems in mathematics. The four most common number system types are:
- Decimal number system
- Binary number system
- Octal number system
- Hexadecimal number system
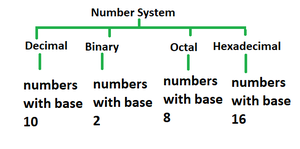
Decimal Number System
Such a number system as has a base value of 10 is termed a decimal number system. It uses the digits between 0 – 9 for the creation of numbers. In this system, each digit is depicted as its product with different powers of 10.
Another feature to be noted is that the place value keeps on increasing from right to left, with the extreme right termed as ones, then tens, hundreds, thousands, and so on. The units (ones) place would be depicted as 100, tens would be 101, hundreds 102, and so on.
For example: 548 has place values as
(5 x 102) + ( 4 x 101) + (8 x 100)
= 5 x 100 + 4 x 10 + 8 x 1
= 500 + 40 + 8
= 548
Binary Number System
As the name suggests, this type of number system has a base value of 2 (binary). This system uses only two digits, i.e., 0 and 1 for creating numbers. Extensively used in computer applications, this system is really east to utilize. For example:
14 can be written as 1110
50 can be written as 110010
Also Read
Octal Number System
As the name suggests, this system has a base value of 8(octal). Hence it uses 8 digits to create numbers. For example:
(112)10 can be expressed as (287)8.
(287)10 can be expressed as (372)8.
Must Check
Hexadecimal Number System
This system has a base value of 16 and hence uses 16 digits for the creation of numbers. For example:
(255)10 can be written as (FF)16
(1096)10 can be written as (448)16
(4090)10 can be written as (FFA)16
What is the importance of the number system?
It is safe and wise to agree that number system holds its importance for everything which includes proportion and percentage. Number system plays a crucial role, both in our everyday lives and the technological world. With its myriad qualities, it simplifies our lives a lot, which has been discussed as follows:
- It enables to keep count of all the things around people. Like how many apples are in the basket, or the number of milk cartons to be purchased, etc.
- It enables the unique and accurate representation of different types of numbers.
- Making a phone call is possible only because we have a proper and efficient number system.
- Elevators used in public places also depend upon number systems for their functioning.
- Computation of any kind of interest on amounts deposited in banks.
- Creation of passwords on computers, security purposes.
- Encrypting important data, by converting figures into another number system to avoid hacking and misuse of data.
- It enables easy conversion of numbers for technical purposes.
- The entirety of computer architecture depends upon number systems (octal, hexadecimal). Every fiber of data gets stored in the computer as a number.
Conceptual Questions
Question 1: Convert 12810 to an octal number.
Solution:
In case of octal conversion, we have to divide the numbers by 8.
| Operation |
Output |
Remainder |
| 128/8 |
16 |
0 |
| 16/8 |
2 |
0 |
| 2/8 |
0 |
2 |
Therefore, the equivalent octal number = 2008
Question 2: Convert 12810 to hexadecimal.
Solution:
In case of hexadecimal conversion, we divide the numbers by 16.
| Operation |
Output |
Remainder |
| 128/16 |
8 |
0 |
| 8/16 |
0 |
8 |
Therefore, the equivalent hexadecimal number is 8016
Question 3: Convert (1101)2 into a decimal number.
Solution:
Now, multiplying each digit from MSB to LSB with reducing the power of the base number 2.
1 × 23 + 1 × 22 + 0 × 21 + 1 × 20
= 8 + 4 + 0 + 1
= 13
Therefore, (1101)2 = (13)10
Question 4: Convert (214)8 into a binary number.
Solution:
We know,
2 → 010
1 → 001
4 → 100
Therefore,(214)8 = (010001100)2
Share your thoughts in the comments
Please Login to comment...