Ways to color a 3*N board using 4 colors
Last Updated :
23 May, 2022
Given a 3 X n board, find the number of ways to color it using at most 4 colors such that no two adjacent boxes have the same color. Diagonal neighbors are not treated as adjacent boxes.
Output the ways%1000000007 as the answer grows quickly.
Constraints:
1<= n < 100000
Examples :
Input : 1
Output : 36
We can use either a combination of 3 colors
or 2 colors. Now, choosing 3 colors out of
4 is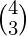 
and arranging them in 3! ways, similarly choosing 2 colors out of 4 is 
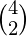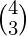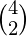and while arrangingwe can only choose which of them could be at centre, that would be 2 ways. Answer = *3! + *2! = 36Input : 2Output : 588
We are going to solve this using dynamic approach because when a new column is added to the board, the ways in which colors are going to be filled depends just upon the color pattern in the current column. We can only have a combination of two colors and three colors in a column. All possible new columns that can be generated is given in the image. Please consider A, B, C and D as 4 colors.
All possible color combinations that can be generated from current column.
From now, we will refer 3 colors combination for a Nth column of the 3*N board as W(n) and two colors as Y(n).
We can see that each W can generate 5Y and 11W, and each Y can generate 7Y and 10W. We get two equation from here
We have two equations now,
W(n+1) = 10*Y(n)+11*W(n);
Y(n+1) = 7*Y(n)+5*W(n);
C++
#include <iostream>
using namespace std;
int solve(int A)
{
long int color3 = 24;
long int color2 = 12;
long int temp = 0;
for (int i = 2; i <= A; i++)
{
temp = color3;
color3 = (11 * color3 + 10 *
color2 ) % 1000000007;
color2 = ( 5 * temp + 7 *
color2 ) % 1000000007;
}
long num = (color3 + color2)
% 1000000007;
return (int)num;
}
int main()
{
int num1 = 1;
cout << solve(num1) << endl;
int num2 = 2;
cout << solve(num2) << endl;
int num3 = 500;
cout << solve(num3) << endl;
int num4 = 10000;
cout << solve(num4);
return 0;
}
|
Java
Python3
def solve(A):
color3 = 24
color2 = 12
temp = 0
for i in range(2, A + 1, 1):
temp = color3
color3 = (11 * color3 + 10 * color2 ) % 1000000007
color2 = ( 5 * temp + 7 * color2 ) % 1000000007
num = (color3 + color2) % 1000000007
return num
if __name__ == '__main__':
num1 = 1
print(solve(num1))
num2 = 2
print(solve(num2))
num3 = 500
print(solve(num3))
num4 = 10000
print(solve(num4))
|
C#
PHP
<div id="highlighter_788133" class="syntaxhighlighter nogutter "><table border="0" cellpadding="0" cellspacing="0"><tbody><tr><td class="code"><div class="container"><div class="line number1 index0 alt2"><code class="plain"><?php</code></div><div class="line number2 index1 alt1"><code class="comments">
|
Javascript
Output :
36
588
178599516
540460643
Time Complexity: O(N), where number of rows = 3 and number of columns = N of the board.
Auxiliary Space: O(1), no extra space required so it is a constant.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...