User Defined Data Structures in Python

In computer science, a data structure is a logical way of organizing data in computer memory so that it can be used effectively. A data structure allows data to be added, removed, stored and maintained in a structured manner. Python supports two types of data structures:

• Non-primitive data types: Python has list, set, and dictionary as its non-primitive data types which can also be considered its in-built data structures.
• User-defined data structures: Data structures that aren’t supported by python but can be programmed to reflect the same functionality using concepts supported by python are user-defined data structures. There are many data structure that can be implemented this way:
  • Linked list
  • Stack
  • Queue
  • Tree
  • Graph
  • Hashmap

Linked list

A linked list is a linear data structure, in which the elements are not stored at contiguous memory locations. The elements in a linked list are linked using pointers as shown in the below image:

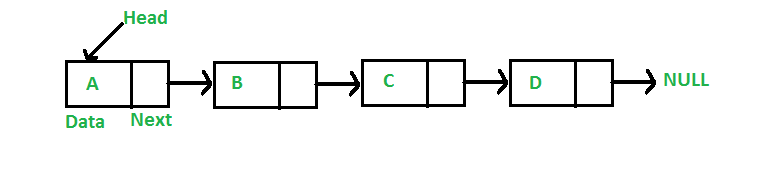
Program:

Python3

llist = ['first', 'second', 'third']
print(llist)

print()

# adding elements
llist.append('fourth')
llist.append('fifth')
llist.insert(3, 'sixth')
print(llist)
print()

llist.remove('second')
print(llist)
print()

Output:

[‘first’, ‘second’, ‘third’]

[‘first’, ‘second’, ‘third’, ‘sixth’, ‘fourth’, ‘fifth’]

[‘first’, ‘third’, ‘sixth’, ‘fourth’, ‘fifth’]

Stack

A stack is a linear structure that allows data to be inserted and removed from the same end thus follows a last in first out(LIFO) system. Insertion and deletion is known as push() and pop() respectively.

Program:

Python3

stack = ['first', 'second', 'third']
print(stack)

print()

# pushing elements
stack.append('fourth')
stack.append('fifth')
print(stack)
print()

# printing top
n = len(stack)
print(stack[n-1])
print()

# popping element
stack.pop()
print(stack)

Output:

[‘first’, ‘second’, ‘third’]

[‘first’, ‘second’, ‘third’, ‘fourth’, ‘fifth’]

fifth

[‘first’, ‘second’, ‘third’, ‘fourth’]

Queue

A queue is a linear structure that allows insertion of elements from one end and deletion from the other. Thus it follows, First In First Out(FIFO) methodology. The end which allows deletion is known as the front of the queue and the other end is known as the rear end of the queue. 

Program:

Python3

queue = ['first', 'second', 'third']
print(queue)

print()

# pushing elements
queue.append('fourth')
queue.append('fifth')
print(queue)
print()

# printing head
print(queue[0])

# printing tail
n = len(queue)
print(queue[n-1])
print()

# popping element
queue.remove(queue[0])
print(queue)

Output:

[‘first’, ‘second’, ‘third’]

[‘first’, ‘second’, ‘third’, ‘fourth’, ‘fifth’]

first

fifth

[‘second’, ‘third’, ‘fourth’, ‘fifth’]

Tree

A tree is a non-linear but hierarchical data structure. The topmost element is known as the root of the tree since the tree is believed to start from the root. The elements at the end of the tree are known as its leaves. Trees are appropriate for storing data that aren’t linearly connected to each other but form a hierarchy. 

Program:

Python3

class node:
    def __init__(self, ele):
        self.ele = ele
        self.left = None
        self.right = None


def preorder(self):
    if self:
        print(self.ele)
        preorder(self.left)
        preorder(self.right)


n = node('first')
n.left = node('second')
n.right = node('third')
preorder(n)

Output:

first

second

third

Graph

A Graph is a non-linear data structure consisting of nodes and edges. The nodes are sometimes also referred to as vertices and the edges are lines or arcs that connect any two nodes in the graph.  A Graph consists of a finite set of vertices(or nodes) and set of Edges which connect a pair of nodes.

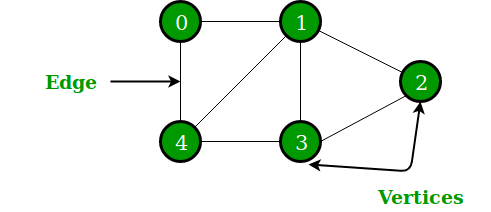
Program:

Python3

class adjnode:
    def __init__(self, val):
        self.val = val
        self.next = None


class graph:
    def __init__(self, vertices):
        self.v = vertices
        self.ele = [None]*self.v

    def edge(self, src, dest):
        node = adjnode(dest)
        node.next = self.ele[src]
        self.ele[src] = node

        node = adjnode(src)
        node.next = self.ele[dest]
        self.ele[dest] = node

    def __repr__(self):
        for i in range(self.v):
            print("Adjacency list of vertex {}\n head".format(i), end="")
            temp = self.ele[i]
            while temp:
                print(" -> {}".format(temp.val), end="")
                temp = temp.next


g = graph(4)
g.edge(0, 2)
g.edge(1, 3)
g.edge(3, 2)
g.edge(0, 3)
g.__repr__()

Output:

Adjacency list of vertex 0

head -> 3 -> 2

Adjacency list of vertex 1

head -> 3

Adjacency list of vertex 2

head -> 3 -> 0

Adjacency list of vertex 3

head -> 0 -> 2 -> 1

Hashmap

Hash maps are indexed data structures. A hash map makes use of a hash function to compute an index with a key into an array of buckets or slots. Its value is mapped to the bucket with the corresponding index. The key is unique and immutable. In Python, dictionaries are examples of hash maps.

Program:

Python3

def printdict(d):
    for key in d:
        print(key, "->", d[key])


hm = {0: 'first', 1: 'second', 2: 'third'}
printdict(hm)
print()

hm[3] = 'fourth'
printdict(hm)
print()

hm.popitem()
printdict(hm)

Output:

0 -> first

1 -> second

2 -> third

0 -> first

1 -> second

2 -> third

3 -> fourth

0 -> first

1 -> second

2 -> third