Sum of the first N Pronic Numbers
Last Updated :
08 Nov, 2022
Given a number N, the task is to find the sum of the first N Pronic Numbers.
The numbers that can be arranged to form a rectangle are called Rectangular Numbers (also known as Pronic numbers).
The first few rectangular numbers are: 0, 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, 156, 182, 210, 240, 272, 306, 342, 380, 420, 462 . . . .
Examples:
Input: N = 4
Output: 20
Explanation: 0, 2, 6, 12 are the first 4 pronic numbers.
Input: N = 3
Output: 8
Approach:
Let, the Nth term be denoted by TN. This problem can easily be solved by splitting each term as follows:
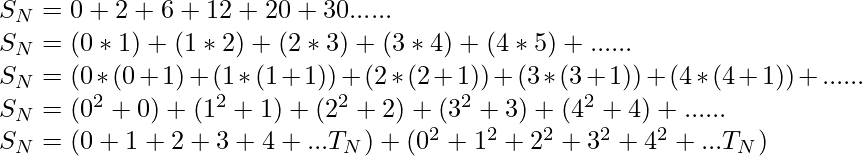
Therefore:
![Rendered by QuickLaTeX.com S_N = Sum of N Pronic Numbers\\ S_N = [N*\frac{(N - 1)}{2}] + [N*\frac{(N - 1)*(2*N - 1)}{6}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a0848bf16e40c8afc949eea631c1e050_l3.png)
C++
#include <bits/stdc++.h>
using namespace std;
int calculateSum(int N)
{
return N * (N - 1) / 2
+ N * (N - 1)
* (2 * N - 1) / 6;
}
int main()
{
int N = 3;
cout << calculateSum(N);
return 0;
}
|
Java
class GFG{
static int calculateSum(int N)
{
return N * (N - 1) / 2 + N * (N - 1) *
(2 * N - 1) / 6;
}
public static void main (String[] args)
{
int N = 3;
System.out.println(calculateSum(N));
}
}
|
Python3
def calculateSum(N):
return (N * (N - 1) // 2 +
N * (N - 1) * (2 *
N - 1) // 6);
N = 3;
print(calculateSum(N));
|
C#
using System;
class GFG{
static int calculateSum(int N)
{
return N * (N - 1) / 2 + N * (N - 1) *
(2 * N - 1) / 6;
}
public static void Main()
{
int N = 3;
Console.Write(calculateSum(N));
}
}
|
Javascript
function calculateSum(N)
{
return Math.floor(N * (N - 1) / 2) + Math.floor(N * (N - 1) * (2 * N - 1) / 6);
}
let N = 3;
console.log(calculateSum(N));
|
Time complexity: O(1).
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...