Subsequences of size three in an array whose sum is divisible by m
Last Updated :
28 Mar, 2023
Given an array A[] (1<=A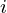 <=10
<=10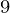 ) of size N (1<=N<=10
) of size N (1<=N<=10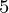 ), find the number of subsequences of length 3 whose sum is divisible by M (1<=M<=10
), find the number of subsequences of length 3 whose sum is divisible by M (1<=M<=10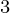 ).
).
Examples:
Input : A[] = {1, 2, 4, 3}
M = 3
Output : 2
Explanation : We can choose two such
subsequence of length 3 such that its
sum is divisible by 3 -> {1, 2, 3} ans
{2, 4, 3}
Brute Force Approach: We use 3 nested loops to traverse all the subsequences of length 3 to count all such subsequence which satisfies the given condition.
Here the brute force solution will work in O(N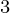 )
)
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
int coutSubSeq(int A[], int N, int M)
{
int sum = 0;
int ans = 0;
for (int i = 0; i < N; i++) {
for (int j = i + 1; j < N; j++) {
for (int k = j + 1; k < N; k++) {
sum = A[i] + A[j] + A[k];
if (sum % M == 0)
ans++;
}
}
}
return ans;
}
int main()
{
int M = 3;
int A[] = { 1, 2, 4, 3 };
int N = sizeof(A)/sizeof(A[0]);
cout << coutSubSeq(A, N, M);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int coutSubSeq(int A[], int N,
int M)
{
int sum = 0;
int ans = 0;
for (int i = 0; i < N; i++) {
for (int j = i + 1; j < N; j++) {
for (int k = j + 1; k < N; k++) {
sum = A[i] + A[j] + A[k];
if (sum % M == 0)
ans++;
}
}
}
return ans;
}
public static void main(String args[])
{
int M = 3;
int A[] = { 1, 2, 4, 3 };
int N = A.length;
System.out.println(coutSubSeq(A, N, M));
}
}
|
Python
def coutSubSeq(A, N,M) :
sum = 0
ans = 0
for i in range(0, N) :
for j in range(i + 1, N) :
for k in range(j + 1, N) :
sum = A[i] + A[j] + A[k]
if (sum % M == 0) :
ans = ans + 1
return ans
M = 3
A = [ 1, 2, 4, 3 ]
N = len(A)
print coutSubSeq(A, N, M)
|
C#
using System;
class GFG {
static int coutSubSeq(int[] A, int N, int M)
{
int sum = 0;
int ans = 0;
for (int i = 0; i < N; i++) {
for (int j = i + 1; j < N; j++) {
for (int k = j + 1; k < N; k++)
{
sum = A[i] + A[j] + A[k];
if (sum % M == 0)
ans++;
}
}
}
return ans;
}
public static void Main()
{
int M = 3;
int []A = { 1, 2, 4, 3 };
int N = A.Length;
Console.WriteLine(coutSubSeq(A, N, M));
}
}
|
PHP
<?php
function coutSubSeq($A, $N, $M)
{
$sum = 0;
$ans = 0;
for ( $i = 0; $i <$N; $i++) {
for ( $j = $i + 1; $j < $N; $j++) {
for ( $k = $j + 1; $k < $N; $k++) {
$sum = $A[$i] + $A[$j] + $A[$k];
if ($sum % $M == 0)
$ans++;
}
}
}
return $ans;
}
$M = 3;
$A = array( 1, 2, 4, 3 );
$N = count($A);
echo coutSubSeq($A, $N, $M);
?>
|
Javascript
<script>
function coutSubSeq(A, N, M)
{
let sum = 0;
let ans = 0;
for (let i = 0; i < N; i++) {
for (let j = i + 1; j < N; j++) {
for (let k = j + 1; k < N; k++) {
sum = A[i] + A[j] + A[k];
if (sum % M == 0)
ans++;
}
}
}
return ans;
}
let M = 3;
let A = [ 1, 2, 4, 3 ];
let N = A.length;
document.write(coutSubSeq(A, N, M));
</script>
|
Second Approach (Efficient for small M):
The above implementation takes a lot of time. So we need a better approach to solve this. Here we will use index mapping (hashing technique) to solve the problem. As we need to check if the sum of the chosen three numbers is divisible by M, we store each value under modulo M. We use a frequency array to store the number of occurrences of each element using index mapping techniques.
Three cases may occur:
- Firstly, if thrice of a number is divisible by M then we will add
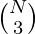 to answer where N is frequency of that number.
to answer where N is frequency of that number. - Secondly, if twice of some number A added with sum number B is divisible by M then we will add
![Rendered by QuickLaTeX.com {{Freq[A]}\choose{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-763579d7c59ec24f2871f187b1b7e731_l3.png) * Freq[B] to the answer.
* Freq[B] to the answer. - Thirdly, if all the numbers A, B, C that sum up to S which is divisible by M then we will add Freq[A] * Freq[B] * Freq[C] to the answer.
With this approach, we can solve the problem in O(M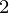 ) which is executable in the given time.
) which is executable in the given time.
Implementation:
C++
#include <iostream>
using namespace std;
int countSubSeq(int A[], int N, int M)
{
int ans = 0;
int h[M] = { 0 };
for (int i = 0; i < N; i++) {
A[i] = A[i] % M;
h[A[i]]++;
}
for (int i = 0; i < M; i++) {
for (int j = i; j < M; j++) {
int rem = (M - (i + j) % M) % M;
if (rem < j)
continue;
if (i == j && rem == j)
ans += h[i] * (h[i] - 1) * (h[i] - 2) / 6;
else if (i == j)
ans += h[i] * (h[i] - 1) * h[rem] / 2;
else if (i == rem)
ans += h[i] * (h[i] - 1) * h[j] / 2;
else if (rem == j)
ans += h[j] * (h[j] - 1) * h[i] / 2;
else
ans = ans + h[i] * h[j] * h[rem];
}
}
return ans;
}
int main()
{
int M = 3;
int A[] = { 1, 2, 4, 3 };
int N = sizeof(A)/sizeof(A[0]);
cout << countSubSeq(A, N, M);
return 0;
}
|
Java
import java.io.*;
import java.util.Arrays;
class GFG {
static int countSubSeq(int A[], int N, int M)
{
int ans = 0;
int h[] = new int[M];
Arrays.fill(h,0);
for (int i = 0; i < N; i++) {
A[i] = A[i] % M;
h[A[i]]++;
}
for (int i = 0; i < M; i++) {
for (int j = i; j < M; j++) {
int rem = (M - (i + j) % M) % M;
if (rem < j)
continue;
if (i == j && rem == j)
ans += h[i] * (h[i] - 1) *
(h[i] - 2) / 6;
else if (i == j)
ans += h[i] * (h[i] - 1) *
h[rem] / 2;
else if (i == rem)
ans += h[i] * (h[i] - 1) *
h[j] / 2;
else if (rem == j)
ans += h[j] * (h[j] - 1) *
h[i] / 2;
else
ans = ans + h[i] * h[j] *
h[rem];
}
}
return ans;
}
public static void main(String args[])
{
int M = 3;
int A[] = { 1, 2, 4, 3 };
int N = A.length;
System.out.println(countSubSeq(A, N, M));
}
}
|
Python
def countSubSeq(A, N, M) :
ans = 0
h = [0] * M
for i in range(0,N) :
A[i] = A[i] % M
h[A[i]] = h[A[i]] + 1
for i in range(0,M) :
for j in range(i,M) :
rem = (M - (i + j) % M) % M
if (rem < j) :
continue
if (i == j and rem == j) :
ans = ans + h[i] * (h[i] - 1) * (h[i] - 2) / 6
elif (i == j) :
ans = ans +( h[i] * (h[i] - 1) * h[rem] / 2)
elif (i == rem) :
ans = ans + h[i] * (h[i] - 1) * h[j] / 2
elif (rem == j) :
ans = ans + h[j] * (h[j] - 1) * h[i] / 2
else :
ans = ans + h[i] * h[j] * h[rem]
return ans
M = 3;
A = [ 1, 2, 4, 3 ]
N = len(A)
print(countSubSeq(A, N, M))
|
C#
using System;
class GFG {
static int countSubSeq(int []A, int N, int M)
{
int ans = 0;
int []h = new int[M];
for (int i = 0; i < N; i++) {
A[i] = A[i] % M;
h[A[i]]++;
}
for (int i = 0; i < M; i++) {
for (int j = i; j < M; j++) {
int rem = (M - (i + j) % M) % M;
if (rem < j)
continue;
if (i == j && rem == j)
ans += h[i] * (h[i] - 1) *
(h[i] - 2) / 6;
else if (i == j)
ans += h[i] * (h[i] - 1) *
h[rem] / 2;
else if (i == rem)
ans += h[i] * (h[i] - 1) *
h[j] / 2;
else if (rem == j)
ans += h[j] * (h[j] - 1) *
h[i] / 2;
else
ans = ans + h[i] * h[j] *
h[rem];
}
}
return ans;
}
public static void Main()
{
int M = 3;
int []A = { 1, 2, 4, 3 };
int N = A.Length;
Console.WriteLine(countSubSeq(A, N, M));
}
}
|
PHP
<?php
function countSubSeq($A, $N, $M)
{
$ans = 0;
$h = array_fill(0, $M, 0);
for ($i = 0; $i < $N; $i++)
{
$A[$i] = $A[$i] % $M;
$h[$A[$i]]++;
}
for ($i = 0; $i < $M; $i++)
{
for ($j = $i; $j < $M; $j++)
{
$rem = ($M - ($i + $j) % $M) % $M;
if ($rem < $j)
continue;
if ($i == $j && $rem == $j)
$ans += $h[$i] * ($h[$i] - 1) *
($h[$i] - 2) / 6;
else if ($i == $j)
$ans += $h[$i] * ($h[$i] - 1) *
$h[$rem] / 2;
else if ($i == $rem)
$ans += $h[$i] * ($h[$i] - 1) *
$h[$j] / 2;
else if ($rem == $j)
$ans += $h[$j] * ($h[$j] - 1) *
$h[$i] / 2;
else
$ans = $ans + $h[$i] *
$h[$j] * $h[$rem];
}
}
return $ans;
}
$M = 3;
$A = array( 1, 2, 4, 3 );
$N = count($A);
echo countSubSeq($A, $N, $M);
?>
|
Javascript
<script>
function countSubSeq(A , N , M)
{
var ans = 0;
var h = Array.from({length: M}, (_, i) => 0);
for (var i = 0; i < N; i++) {
A[i] = A[i] % M;
h[A[i]]++;
}
for (var i = 0; i < M; i++) {
for (var j = i; j < M; j++) {
var rem = (M - (i + j) % M) % M;
if (rem < j)
continue;
if (i == j && rem == j)
ans += h[i] * (h[i] - 1) *
(h[i] - 2) / 6;
else if (i == j)
ans += h[i] * (h[i] - 1) *
h[rem] / 2;
else if (i == rem)
ans += h[i] * (h[i] - 1) *
h[j] / 2;
else if (rem == j)
ans += h[j] * (h[j] - 1) *
h[i] / 2;
else
ans = ans + h[i] * h[j] *
h[rem];
}
}
return ans;
}
var M = 3;
var A = [ 1, 2, 4, 3 ];
var N = A.length;
document.write(countSubSeq(A, N, M));
</script>
|
complexity analysis:
The time complexity of the given program is O(M^2) as it has two nested loops iterating over the range [0, M).
The space complexity is O(M) as an array of size M is created to store the frequencies of remainders when divided by M.
Share your thoughts in the comments
Please Login to comment...