Spherical Capacitor Formula

Last Updated : 04 Feb, 2024

A capacitor is simply an electric device that consists of two terminals that have the ability to store energy in the form of an electric charge. It can be designed by simply placing two electrical conductors at a distance from each other. The empty space between the conductors may be filled by vacuum(or air) or with an insulating material known as a dielectric. The ability of the capacitor to store charges is known as capacitance.

In a capacitor, the two terminals having opposite charges are placed at a distance from each other which allows it to generate(store) energy. The simplest design for a capacitor is a parallel plate, which consists of two metal plates with a gap between them. It should be noted that a capacitor can be of any shape or size or be made of any material until its terminals store opposite charges and thus store energy.

Capacitance of a capacitor

Consider a capacitor whose positive and negative plates hold +q and -q charge respectively. A DC voltage source is applied across it which gives it a potential difference of V across the plates. Now as we know,

Q α V

Putting a constant C in this relation.

Q=CV.

Note: The capacitance of every material is unique and its SI unit is Farad(F).

Working of a capacitor

Let’s suppose that we are given the most basic form of the capacitor, which is a parallel plate capacitor. It consists of two parallel plates separated by a small distance and that gap is filled by a dielectric. Next, we are given a DC voltage source that is linked across the capacitor, where one plate is attached to the positive end (plate I) and the other plate is connected to the negative end (plate II). When the battery’s potential is applied across the capacitor, plate I become positive in relation to plate II. At steady-state, current attempts to pass through the capacitor from the positive plate to the negative plate. However, because of a gap between them with an insulating layer(dielectric), it is unable to flow.

Structure of a simple capacitor.

For some time the capacitor continues to get charged by the incoming flow of the current. But after some time it reaches a state where it holds the maximum amount of charge that it can possibly hold. This is how a capacitor stores energy The time taken to reach this state of maximum charge is called the charging time of the capacitor. Later we disconnect the voltage source from the circuit and insert a load resistor in it. Now the current starts flowing from the positively charged terminal of the capacitor to the negatively charged terminal and loses all of its energy in the process. This time period is called the discharging time of the capacitor.

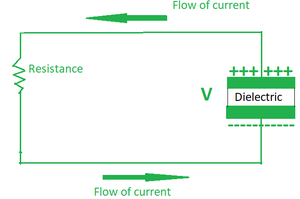
Discharging of a capacitor.

Spherical Capacitor Formula

As mentioned earlier capacitance occurs when there is a separation between the two plates. So for constructing a spherical capacitor we take a hollow sphere such that the inner surface is positively charged and the outer surface of the sphere is negatively charged. The inner radius of the sphere is r and the outer radius is given by R. The distance of R-r between the two oppositely charged surfaces acts as the dielectric. Let’s assume that the inner spherical surface has a potential of V₁ and V_2.

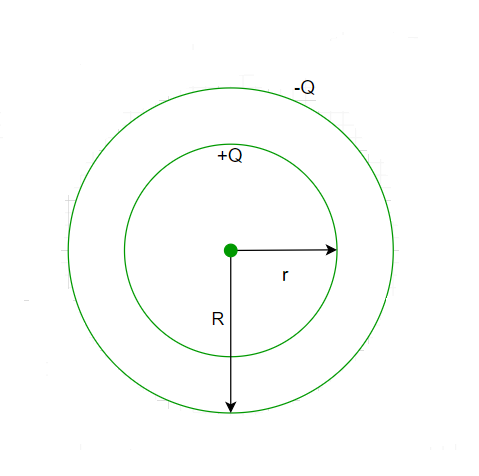
A spherical capacitor

Next, the electric field generated by a charged sphere (hollow) of radius r having charge Q is given by,

E= $\frac{Q}{4π∈_0r^2}$ . ⇢ (1)

Also, we know that the Electric field generated is related to the potential difference as,

E= $-\frac{dV}{dr}$ . ⇢ (2)

Comparing (1) and (2),

$-\frac{dV}{dr} =\frac{Q}{4π∈_0r^2}$

$-dV= \frac{Qdr}{4π∈_0r^2}$

Integrating on both sides within the limits V, V and r, R.

$\int_{V_1}^{V_2} -dV = \int_{r}^{R} \frac{Q}{4π∈_0r^2}dr$

$\int_{V_1}^{V_2}-dV = \frac{Q}{4π∈_0} \int_{r}^{R} \frac{dr}{r^2}$

$-[V] |_{V_1}^{V_2} = \frac{Q}{4π∈_0} \frac{-r^{-2}+1}{-2+1}|_{r}^{R}$

$[V_2 -V_1] = \frac{Q}{4π∈_0} [\frac{1}{R}-\frac{1}{R}]$

$\Delta = \frac{Q}{4π∈_0} [\frac{1}{R}-\frac{1}{R}]$ ⇢ (3)

$\Delta$ is the change in potential as we move from inside the sphere to outside. Now the capacitance of a capacitor is given by,

$C= \frac{Q}{\Delta V}$ ⇢ (4)

Comparing (3) and (4),

$C = \frac{Q}{\frac{Q}{4π∈_0}(\frac{1}{R} - \frac{1}{r})}$

$C = \frac{Q4π∈_0}{Q[\frac{1}{R} - \frac{1}{r}]}$

Simplifying further we get,

$C = 4π∈_0 (\frac{rR}{r-R})$

Since capacitance can’t be negative the positive value is taken. This is the expression for the capacitance of a spherical capacitor.

Sample Questions

Question 1: A spherical capacitor has an inner radius of 7 cm and an outer radius of 10 cm. Find the capacitance of the sphere. Assume the dielectric in between to be air.

Solution:

The capacitance of the sphere is given by,

C = $4π∈_0 (\frac{rR}{r-R})$

Here ∈₀ = 8.85 × 10^-12, r = 7, R = 10

C= $\frac{4\times3.14\times8.85\times10^{-12} \times70\times10^{-2}}{(10-7)10^{-1}}$

C = 2.593 × 10^-12F

Question 2: In the above problem find how much charge will it take for the capacitor to raise its potential from 0 to10,000 V.

Solution:

The capacitance of the spherical capacitor is C = 2.593 × 10^-12F.

The charge required can be found by using Q = CV. where V is the potential difference.

Potential difference V in this case is 1000-0 = 1000V

Therefore, Q = 3.7052 × 10^-12 × 1000

Q = 2.593 × 10^-9C

Question 3: The inner radius of a spherical capacitor is x m and its outer radius is 5/4 x m if the outer radius is increased to 3/2x m, find by what ratio its capacitance is changed.

Solution:

In this case $C_1 =4π∈_0(\frac{rR}{R-r})$

= $4π∈_0(\frac{x\frac{5x}{4}}{\frac{5}{4}x -x})$

= 20 πε_ox F

$C_2 = 4π∈_0(\frac{x\frac{3x}{2}}{\frac{3x}{2}-{x}})$

= 20 πε_ox F

$\frac{C_1}{C_2} =\frac{ 20 π∈_0 x }{12 π∈_0x}$

$\frac{C_1}{C_2} =\frac{5}{3}$

So the capacitance decreases as the external radius is increased.

Question 4: A sphere has a radius of 10 cm. find the capacitance on it and also find the potential difference required to give it a charge of 10^-8 C.

Solution:

C = 4 πε_ox F

C = 4 × 3.14 × 8.85 × 10⁻¹² × 10 × 10⁻²

C = 111.156 × 10⁻¹³

C = 1.11 × 10⁻¹¹ F

Now Q = CV

Therefore $V = \frac{10^{-8}}{1.11x10^{-11}}$

Hence V = 900.9 V

Question 5: The outer radius of a spherical capacitor is 10 % bigger than its inner radius. The capacitance of this capacitor is 10^-8 F. Find the value of its inner and outer radii.

Answer:

$C = 4π∈_0 (\frac{rR}{r-R})$

Here r = x, R = 1.1x and C= 10^-8 F

So, $C = \frac{1.1x(x)}{1.1x-x}$

$10^{-12}=4\pi\epsilon\frac{1.1x^2}{0.1x}$

$11x =\frac{10^{-12}}{4\pi\epsilon}$

x = 0.009 m

So the inner radius is 0.09 cm and the outer radius is 0.099 cm.

Question 6: The inner and outer radii of a spherical capacitor are 5cm and 6cm. Find the energy of the capacitor if a potential difference of 1000V is applied to it.

Solution:

The capacitance of this capacitor is calculated as,

$C = 4{\pi}{\epsilon}{\frac{6\times5\times10^{-2}}{(6-5)\times10^{-1}}}$

C = 3.3363 × 10⁻¹² F

U = 1/2 CV²

U = 21 × 3.3363 × 10⁻¹²× (1000)²

U = 1.66815 × 10⁻⁹ J

Question 7: A spherical capacitor of inner and outer radii 8cm and 10cm has an energy of 10^-8 J . Find its Voltage.

Solution:

Lets find the capacitance first,

$C = 4\pi\epsilon\frac{8\times10\times10^{-2}}{(10-8)\times10^{-1}}$

C = 4.446 × 10^-9 F

U = 1/2 CV²

$V =\sqrt {\frac{2U}{C}}$

$V=\sqrt{\frac{2\times{10^{-8}}}{4.446\times 10^{-9}}}$

V = 2.12 V