Sparse Inverse Covariance Estimation in Scikit Learn
Last Updated :
02 Jan, 2023
Sparse inverse covariance (also known as the precision matrix) is a statistical technique used to estimate the inverse covariance matrix of a dataset. The goal of this technique is to find a sparse estimate of the precision matrix, which means that many of the entries in the matrix are set to zero. This can be useful for identifying relationships between variables in the data and for building more interpretable models.
The precision matrix is the inverse of the covariance matrix, which is a measure of the correlations between the variables in the dataset. The covariance matrix is typically estimated using the sample covariance, which is an unbiased estimator of the population covariance. The sample covariance is defined as follows:
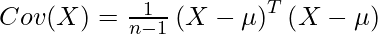
where X is the data matrix, n is the number of samples, and mu is the mean vector.
The precision matrix is the inverse of the covariance matrix, which can be computed as follows:
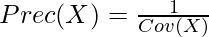
The goal of sparse inverse covariance estimation is to find a sparse estimate of the precision matrix, which means that many of the entries in the matrix are set to zero. This can be achieved using regularized maximum likelihood estimation, such as the graphical Lasso algorithm. This algorithm estimates the precision matrix by minimizing a penalized log-likelihood function that encourages sparsity in the estimated matrix.
Sparse Inverse Covariance Estimation in Scikit Learn
One way to perform sparse inverse covariance estimation is to use the graphical Lasso algorithm, which is a type of regularized maximum likelihood estimation. The graphical Lasso algorithm estimates the precision matrix by minimizing a penalized log-likelihood function that encourages sparsity in the estimated matrix. This can be implemented using the GraphicalLasso class in sklearn.covariance module in scikit-learn.
Here is an example of how to use the GraphicalLasso class to perform sparse inverse covariance estimation in scikit-learn:
Python3
import numpy as np
from sklearn.covariance import GraphicalLasso
X = np.random.randn(100, 10)
estimator = GraphicalLasso()
estimator.fit(X)
precision_matrix = estimator.precision_
print(precision_matrix)
|
Output:
[[ 0.97175596 0.01130831 0.11017201 -0.00430963 0.08559263 0.1237138
-0.13820535 -0.0129074 -0.08665746 -0.01677981]
[ 0.01130831 1.21991013 0.20705554 -0.04488101 -0.04271241 0.01814005
0.01748837 -0.17626741 -0.11433033 -0.2362835 ]
[ 0.11017201 0.20705554 1.22388602 -0.12417476 -0.01734046 0.06019758
-0.02174498 -0.04635053 -0.0745821 -0.17048511]
[-0.00430963 -0.04488101 -0.12417476 0.96789315 -0.08847719 -0.05228502
0.14320472 0.09072693 -0.12536907 0.13996888]
[ 0.08559263 -0.04271241 -0.01734046 -0.08847719 1.02920436 0.1514347
0.02841566 -0.09214423 -0.00709575 -0.03294409]
[ 0.1237138 0.01814005 0.06019758 -0.05228502 0.1514347 0.98480463
-0.04031905 -0.19720552 -0.00253548 -0.13368934]
[-0.13820535 0.01748837 -0.02174498 0.14320472 0.02841566 -0.04031905
1.21715663 -0.12172663 0.17423586 -0.0475109 ]
[-0.0129074 -0.17626741 -0.04635053 0.09072693 -0.09214423 -0.19720552
-0.12172663 1.05062603 -0.16604791 0.27156971]
[-0.08665746 -0.11433033 -0.0745821 -0.12536907 -0.00709575 -0.00253548
0.17423586 -0.16604791 1.18931358 0.00268037]
[-0.01677981 -0.2362835 -0.17048511 0.13996888 -0.03294409 -0.13368934
-0.0475109 0.27156971 0.00268037 1.02405594]]
This code will fit a GraphicalLasso estimator to the random data and obtain the estimated precision matrix. The precision_ attribute of the estimator contains the estimated precision matrix.
You can also specify hyperparameters for the GraphicalLasso estimator, such as the regularization parameter alpha and the convergence tolerance tol. For example:
Python3
estimator = GraphicalLasso(alpha=0.01,
tol=0.001)
estimator.fit(X)
|
Output:
GraphicalLasso(tol=0.001)
This code will create a GraphicalLasso estimator with the specified alpha and tol values and fit it to the data. The optimal values for these hyperparameters will depend on the specific dataset and should be determined through cross-validation or other model selection techniques.
Share your thoughts in the comments
Please Login to comment...