Simplify x – 1/x
Last Updated :
21 Nov, 2021
Mathematics has been a part of human development since the time human civilization exists. Initially, it was used for basic calculations. Later on, mathematics made its mark and was further developed into various branches based on the type of analysis. Such as geometry was developed to calculate parameters of objects, arithmetic for trading, etc.
Among the subdivisions of mathematics, algebra is the one that deals with numbers, symbols, and their basic operations. Algebraic expressions are equations that consist of constants, variables, and coefficients. And, The combination of these three components is known as terms. The terms are associated with the basic mathematical operation to form and expression.
Basic algebraic formulas
- a² – b² = (a – b)(a + b)
- (a + b)² = a² + 2ab + b²
- (a – b)² = a² – 2ab + b²
- a² + b² = (a – b)² + 2ab.
- (a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc.
- (a – b – c)² = a² + b² + c² – 2ab – 2ac + 2bc.
- a³ – b³ = (a – b)(a² + ab + b²)
- a³ + b³ = (a + b) (a² – ab + b²)
Simplify x – 1/x
Solution:
Given,
x – 1/x
=>By using LCM method
=>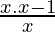
=>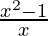
By the formula (a+b)(a-b)=a2-b2
The formula is derived as
=>(a+b)(a-b)
=>a.a – ab + ab – b.b
Cancelling -ab and +ab
=>a2 – b2
As per the derived algebraic formula the solution would be
=>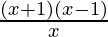
Sample Problems
Question 1. If x + 1/x = 3. Find the value of x2 + 1/x2.
Answer:
Given,
x + 1/x = 3
Then, squaring on both sides
=> (x + 1/x)2 = (3)2
=> x2 + 2.x.1/x + (1/x)2 = 9
=> x2 + 1/x2 + 2 = 9
=> x2 + 1/x2 = 7
Question 2. Simplify 3/(x-1)+1/x(x-1) = 2/x
Answer:
3/(x-1)+1/x(x-1) = 2/x
Taking common denominator
=> 3x + 1/x(x-1) = 2(x-1)/x(x-1)
=> 3x + 1 = 2(x-1)
=> x = -3
Question 3. If x + 1/x = 2. Find the value of x.
Answer:
x + 1/x = 2
=> x2 + 1/x = 2
=> x2 + 1 = 2x
=> x2 – 2x + 1 = 0
=> (x – 1)2 = 0
=> x – 1 = 0
=> x = 1
Question 4. If x + 1/x = 9 then what will be x3 + 1/x3?
Solution:
Given,
x + 1/x = 9
Taking cube on both sides of the equation
=> (x+1/x)3=(9)3
=> x3+1/x3+3x.1/x(x+1/x)=729
=> x3+1/x3+3.9=729
=> x3+1/x3=729-27
= x3+1/x3=702
Question 5. If x + 1/x = 3 then, what will be x3 + 1/x3?
Solution:
Given,
=>(x+1/x)3=(3)3
=>x3+3.x2.1/x+3.x.1/x2+1/x3=27
=>(x3+1/x3)+3(x+1/x)=27
=>x3+1/x3+3 x 3=27
=>x3+1/x3=27-9
=>x3+1/x3=18
Share your thoughts in the comments
Please Login to comment...