How to use DeMoivre’s theorem to simplify (1 + √3i)6?

Complex numbers are the numbers of the form a + ib, such that a and b are real numbers and i (iota) is the imaginary component and represents √(-1), commonly depicted in their rectangular or standard form. For example, 10 + 5i is a complex number where 10 is the real part and 5i is the imaginary part. These can be purely real or purely imaginary depending upon the values of a and b. If a = 0 in a + ib, then ib is a purely imaginary number, and if b = 0, then we have a, which is a purely real number. 

Modulus and Polar form of Complex numbers

The non-negative square root of the sum of squares of the real and imaginary part of a complex number is termed its modulus. Modulus is depicted as mod(z) or |z| or |x + iy| and is defined for a complex number z = a + ib as,

mod(z) or |z| =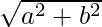 

Here, the polar coordinates of the real and imaginary parts are written to depict a complex number. The angle at which the number line is inclined to the real axis, i.e., the x-axis, is represented by θ. The length represented by the line is called its modulus and is depicted by the alphabet r. The figure below depicts a and b as the real and imaginary components respectively and OP = r is the modulus.

For a complex number of the form z = p + iq, its polar form is written as follows,

r = Modulus[cos(argument) + isin(argument)]

Or, z = r[cosθ + isinθ]

Here, r = 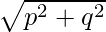 and θ = tan^-1{q/p}.

How to use DeMoivre’s theorem to simplify (1 + √3i)⁶?

Solution:

In order to expand a complex number as per its given exponent, it first needs to be converted into its polar form, which uses its modulus and argument as its constituents. Then, DeMoivre’s theorem is applied, which states the following,

De Moivre’s Formula: For all real values of say, a number x,

(cos x + isinx)ⁿ = cos(nx) + isin(nx), where n is any integer.

Given number: (1 + √3i)⁶

Modulus of (1 + √3i)⁶ = 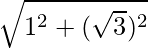 = 2

Argument = tan^-1(√3/1) = tan^-1(√3) = π/3

⇒ Polar form = 

Now, (1 + √3i)⁶ = 

As per DeMoivre’s theorem, (cos x + i sinx)ⁿ = cos(nx) + i sin(nx). 

⇒  = 

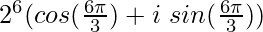
= 64 (cos 2π + i sin 2π)

= 64(1 + 0)

= 64

Hence, (1 + √3i)⁶ = 64

Similar Problems

Question 1: Expand: (1 + i)⁵.

Solution:

Here, r = 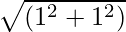 = 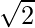, θ = π/4

The polar form of (1 + i) = 

According to De Moivre’s Theorem: (cosθ + sinθ)ⁿ = cos(nθ) + i sin(nθ).

Thus, (1 + i)⁵ = 

= 

= -4 – 4i

Hence, (1 + i)⁵ = -4 – 4i.

Question 2: Expand: (2 + 2i)⁶.

Solution:

Here, r = 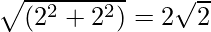, θ = π/4

The polar form of  (2 + 2i) = 

According to De Moivre’s Theorem: (cosθ + sinθ)ⁿ = cos(nθ) + i sin(nθ).

Thus, (2 + 2i)⁶ = 

= 

= 512 (-i)

Hence, (2 + 2i)⁶ = −512i.

Question 3: Expand: (1 + i)¹⁸.

Solution:

Here, r = 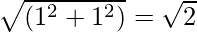, θ = π/4

The polar form of (1+i) = 

According to De Moivre’s Theorem: (cosθ + sinθ)ⁿ = cos(nθ) + i sin(nθ).

Thus, (1 + i)¹⁸ = 

= 

= 512i

Hence, (1 + i)¹⁸ = 512i.

Question 4: Expand: (-√3 + 3i)³¹.

Solution:

Here, r = 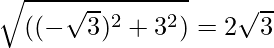, θ = π/4

The polar form of  (-√3 + 3i) = 

According to De Moivre’s Theorem: (cosθ + sinθ)ⁿ = cos(nθ) + i sin(nθ).

Thus, (-√3 + 3i)³¹= 

Hence, (-√3 + 3i)³¹ =

Question 5: Expand: (1 – i)¹⁰.

Solution:

r = , θ = π/4

The polar form of  (1 – i) = 

According to De Moivre’s Theorem: (cosθ + sinθ)ⁿ = cos(nθ) + i sin(nθ).

Thus, (1 – i)¹⁰ = 

= 32 [0 – i(1)]

= 32 (-i)

Hence, (1 – i)¹⁰ = 0 – 32i.