Shift all prefixes by given lengths
Last Updated :
06 Dec, 2022
Given a string S containing letters and digits, and an integer array Shift where, 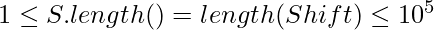 and for each element of Shift array
and for each element of Shift array ![Rendered by QuickLaTeX.com 0 \leq Shift[i] \leq 10^{9}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-eb9e5d7d710aec172109c7c7771aad61_l3.png) . The task is, for each Shift[i] = X, you have to shift the first i+1 letters of S, X times. Return the final string after all applying all such shift to S.
. The task is, for each Shift[i] = X, you have to shift the first i+1 letters of S, X times. Return the final string after all applying all such shift to S.
Note: Shift means cyclically increment ASCII value.
Examples:
Input: S = “abc789”, Shift = [2, 5, 9]
Output: “qpl706”
Explanation: Starting with “abc”.
After shifting the first 1 letters of S by 2, we have “cbc”.
After shifting the first 2 letters of S by 5, we have “hgc”.
After shifting the first 3 letters of S by 9, we have “qpl”.
Input : S = “geeksforgeeks”, Shift[] = [ 11, 10000, 9999999 ]
Output : qdnyulaufkuug
Approach: The i-th character of S is shifted Shift[i] + Shift[i+1] + … + Shift[Shift.length – 1] times.
So we update the Shift array backward to know the exact number of shifts to be applied to each element of string S.
Now,
- Traverse the given text (S) one character at a time.
- For each character, transform the given character as per the rule, i:e apply shift, Shift[i] times.
- Return the new string generated.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
string shift_S(string S, int Shift[], int n)
{
for (int i = n - 2; i >= 0; --i)
Shift[i] += Shift[i + 1];
string result = "";
for (int i = 0; i < S.length(); i++) {
if (isupper(S[i])) {
result += char((int(S[i]) + Shift[i] - 'A') % 26 + 'A');
}
else if (islower(S[i])) {
result += char((int(S[i]) + Shift[i] - 'a') % 26 + 'a');
}
else {
result += char((int(S[i]) + Shift[i] - '0') % 10 + '0');
}
}
return result;
}
int main()
{
string S = "abc";
int Shift[] = { 2, 5, 9 };
int n = sizeof(Shift) / sizeof(Shift[0]);
cout << shift_S(S, Shift, n);
return 0;
}
|
Java
public class GfG{
public static String shift_S(String S, int Shift[], int n)
{
for (int i = n - 2; i >= 0; --i)
Shift[i] += Shift[i + 1];
String result = "";
for (int i = 0; i < S.length(); i++) {
if (Character.isUpperCase(S.charAt(i))) {
result += (char)(((int)(S.charAt(i)) + Shift[i] - 'A') % 26 + 'A');
}
else if (Character.isLowerCase(S.charAt(i))) {
result += (char)(((int)(S.charAt(i)) + Shift[i] - 'a') % 26 + 'a');
}
else {
result += (char)(((int)(S.charAt(i)) + Shift[i] - '0') % 10 + '0');
}
}
return result;
}
public static void main(String []args){
String S = "abc";
int Shift[] = { 2, 5, 9 };
int n = Shift.length;
System.out.println(shift_S(S, Shift, n));
}
}
|
Python3
def shift_S(S, Shift, n):
for i in range(n - 2, -1, -1):
Shift[i] = Shift[i] + Shift[i + 1]
result = ""
for i in range(len(S)):
if(S[i].isupper()):
result = result + chr((ord(S[i]) + Shift[i] -
ord('A')) % 26 + ord('A'))
elif (S[i].islower()):
result = result + chr((ord(S[i]) + Shift[i] -
ord('a')) % 26 + ord('a'))
else:
result = result + chr((ord(S[i]) + Shift[i] -
ord('0')) % 10 + ord('0'))
return result
S = "abc"
Shift = [2, 5, 9]
n = len(Shift)
print(shift_S(S, Shift, n))
|
C#
using System;
class GfG{
public static String shift_S(string S,
int[] Shift,
int n)
{
for(int i = n - 2; i >= 0; --i)
Shift[i] += Shift[i + 1];
string result = "";
for(int i = 0; i < S.Length; i++)
{
if (Char.IsUpper(S[i]))
{
result += (char)(((int)(S[i]) +
Shift[i] - 'A') % 26 + 'A');
}
else if (Char.IsLower(S[i]))
{
result += (char)(((int)(S[i]) +
Shift[i] - 'a') % 26 + 'a');
}
else
{
result += (char)(((int)(S[i]) +
Shift[i] - '0') % 10 + '0');
}
}
return result;
}
public static void Main()
{
string S = "abc";
int[] Shift = { 2, 5, 9 };
int n = Shift.Length;
Console.WriteLine(shift_S(S, Shift, n));
}
}
|
Javascript
<script>
function shift_S(S, Shift, n){
for(let i = n - 2;i>=0;i--){
Shift[i] = Shift[i] + Shift[i + 1]
}
let result = ""
for(let i=0;i<S.length;i++){
if(S.charCodeAt(i) >= 65 && S.charCodeAt(i) <= 90)
result = result + String.fromCharCode((S.charCodeAt(i) + Shift[i] -'A'.charCodeAt(0)) % 26 + 'A'.charCodeAt(0))
else if (S.charCodeAt(i) >= 97 && S.charCodeAt(i) <= 122)
result = result + String.fromCharCode((S.charCodeAt(i) + Shift[i] -'a'.charCodeAt(0)) % 26 + 'a'.charCodeAt(0))
else
result = result + String.fromCharCode((S.charCodeAt(i) + Shift[i] -'0'.charCodeAt(0)) % 26 + '0'.charCodeAt(0))
}
return result
}
let S = "abc"
let Shift = [2, 5, 9]
let n = Shift.length
document.write(shift_S(S, Shift, n))
</script>
|
Time Complexity: O(N), where N is the length of string S.
Auxiliary Space: O(N)
Share your thoughts in the comments
Please Login to comment...