Set Notations in LaTeX
Last Updated :
15 Apr, 2024
Set notation –
In set theory and its applications to logic, mathematics, and computer science, set-builder notation is a mathematical notation for describing a set by enumerating its elements or stating the properties that its members must satisfy. For example, empty set is represented as
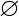
. So Let’s see the latex code of Set Notations one by one.
Set notation and their Latex Code :
TERM
| SYMBOL
| LaTeX
|
|---|
Empty Set
| ∅ or {}
| \emptyset or \{\}
|
|---|
Universal Set
| U
| \mathbb{U}
|
|---|
Subset
| ⊆ or ⊂
| \subseteq or \subset
|
|---|
Proper Subset
|
⊂
| \subset
|
|---|
Superset
| ⊇ or ⊃
| \supseteq or \supset
|
|---|
Proper Superset
|
⊃
| \supset
|
|---|
Element
|
∈
| \in
|
|---|
Not an Element
|
∉
| \notin
|
|---|
Union
|
∪
| \cup
|
|---|
Intersection
|
∩
| \cap
|
|---|
Complement
|
\
| \complement
|
|---|
Set Difference
|
\
| \setminus
|
|---|
Power Set
|
℘
| \wp
|
|---|
Cartesian Product
|
×
| \times
|
|---|
Cardinality
|
| A
|
|---|
Set Builder Notation
| { x | P(x) }
| \{ x | P(x) \}
|
|---|
Set Membership Predicate
| P(x) ∈ A
| P(x) \in A
|
|---|
Set Minus
| A – B
| A – B
|
|---|
Set Inclusion Predicate
| A ⊆ B
| A \subseteq B
|
|---|
Set Equality
| A = B
| A = B
|
|---|
Disjoint Sets
| A ∩ B = ∅
| A \cap B = \emptyset
|
|---|
Subset Not Equal to
| A ⊊ B
| A \subsetneq B
|
|---|
Superset Not Equal to
| A ⊋ B
| A \supsetneq B
|
|---|
Symmetric Difference
| A Δ B
| A \triangle B
|
|---|
Subset of or Equal to
| A ⊆ B or A = B
| A \subseteq B \text{ or } A = B
|
|---|
Proper Subset of or Equal to
| A ⊆ B but A ≠ B
| A \subseteq B \text{ but } A \neq B
|
|---|
Cartesian Power
| A^n
| A^{n}
|
|---|
Union of Sets
| ⋃ A
| \bigcup A
|
|---|
Intersection of Sets
| ⋂ A
| \bigcap A
|
|---|
Cartesian Product of Sets
| ⨉ A
| \bigtimes A
|
|---|
Set of All Functions from A to B
| B^A
| B^{A}
|
|---|
Set of All Relations from A to B
| A×B
| A \times B
|
|---|
Share your thoughts in the comments
Please Login to comment...