RSA and Digital Signatures
Last Updated :
07 May, 2023
Digital Signature : As the name sounds are the new alternative to sign a document digitally. It ensures that the message is sent by the intended user without any tampering by any third party (attacker). In simple words, digital signatures are used to verify the authenticity of the message sent electronically.
RSA : It is the most popular asymmetric cryptographic algorithm. It is primarily used for encrypting message s but can also be used for performing digital signature over a message. Let us understand how RSA can be used for performing digital signatures step-by-step. Assume that there is a sender (A) and a receiver (B). A wants to send a message (M) to B along with the digital signature (DS) calculated over the message. Step-1 : Sender A uses SHA-1 Message Digest Algorithm to calculate the message digest (MD1) over the original message M.
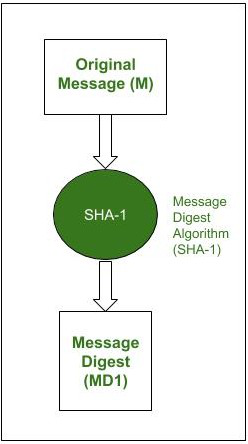
Message digest calculation
Step-2 : A now encrypts the message digest with its private key. The output of this process is called Digital Signature (DS) of A.

Digital signature creation
Step-3 : Now sender A sends the digital signature (DS) along with the original message (M) to B.

Transmission of original message and digital signature simultaneously
Step-4 : When B receives the Original Message(M) and the Digital Signature(DS) from A, it first uses the same message-digest algorithm as was used by A and calculates its own Message Digest (MD2) for M.

Receiver calculates its own message digest
Step-5 : Now B uses A’s public key to decrypt the digital signature because it was encrypted by A’s private key. The result of this process is the original Message Digest (MD1) which was calculated by A.

Receiver retrieves sender’s message digest
Step-6 : If MD1==MD2, the following facts are established as follows.
- B accepts the original message M as the correct, unaltered message from A.
- It also ensures that the message came from A and not someone posing as A.

Digital signature verification
The message digest (MD1) was encrypted using A’s private key to produce a digital signature. Therefore, the digital signature can be decrypted using A’s public key (due to asymmetric form of RSA). If the receiver B is able to decrypt the digital signature using A’s public key, it means that the message is received from A itself and now A cannot deny that he/she has not sent the message. It also proves that the original message did not tamper because when the receiver B tried to find its own message digest MD2, it matched with that of A’s MD1. Suppose a malicious user tries to access the original message and perform some alteration. Now he/she will calculate a new message digest over the altered message. It might concern you with data integrity and confidentiality but here’s the catch. The attacker will have to sign the altered message using A’s private key in order to pose as A for the receiver B. However, an attacker cannot sign the message with A’s private key because it is known to A only. Hence, the RSA signature is quite strong, secure, and reliable. Attacks on RSA Signature : There are some attacks that can be attempted by attackers on RSA digital signatures. A few of them are given below as follows.
- Chosen-message Attack – In the chosen-message attack, the attacker creates two different messages, M1 and M2, and somehow manages to persuade the genuine user to sign both the messages using RSA digital-signature scheme. Let’s consider message M1 and message M2. so, the attacker computes a new message M = M1 x M2 and then claims that the genuine user has signed message M.
- Key-only Attack – In this attack, the Assumption is that attacker has access to the genuine user public key and tries to get a message and digital signature. OnlyThe attacker then tries to create another message MM such that the same signature S looks to be valid on MM. However, it is not an easy attack to launch since the mathematical complexity beyond this is quite high.
- Known-message Attack – In a known-message attack, the attacker tries to use a feature of RSA whereby two different messages having two different signatures can be combined so that their signatures also combine. To take an example, let us say that we have two different messages M1 and M2 with respective digital signatures as S1 and S2. Then if M = (M1 x M2) mod n, mathematically S = (S1 ¥ S2) mod n. Hence, the attacker can compute M = (M1 x M2) mod n and then S = (S1 x S2) mod n to forge a signature.
RSA is a widely used algorithm for digital signatures because it provides strong security and efficient performance. Digital signatures are used to verify the authenticity of digital documents and ensure that they have not been tampered with. The process of creating a digital signature involves the following steps:
- Hashing: The first step in creating a digital signature is to create a hash of the message or document that needs to be signed. This is done using a hash function, which produces a fixed-length output (the hash value) from an input of any size.
- Signing: The hash value is then encrypted using the private key of the signer. This produces the digital signature, which is attached to the original message or document.
- Verification: To verify the authenticity of the digital signature, the recipient of the message or document must first decrypt the signature using the public key of the signer. This produces the original hash value. The recipient then calculates the hash value of the received message or document using the same hash function that was used by the signer. If the two hash values match, the signature is valid and the message or document has not been tampered with.
- RSA is well-suited for digital signatures because it provides strong security and efficient performance. The security of RSA is based on the difficulty of factoring large prime numbers. In RSA, the private key is a pair of prime numbers, and the public key is a product of these primes. Because factoring the public key into its prime factors is considered a computationally difficult problem, it is infeasible for an attacker to deduce the private key from the public key.
- Furthermore, RSA is efficient because the signing process only involves modular exponentiation, which is a relatively fast operation. This makes it suitable for use in a wide range of applications, including digital certificates, secure email, and electronic commerce.
In summary, RSA is a popular algorithm for digital signatures because it provides strong security and efficient performance. Digital signatures are important for verifying the authenticity of digital documents and ensuring that they have not been tampered with.
Share your thoughts in the comments
Please Login to comment...